21.2.1.1 直接开平方法 课件(17张PPT)
文档属性
| 名称 | 21.2.1.1 直接开平方法 课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 997.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 10:45:31 | ||
图片预览




文档简介
(共17张PPT)
21.2.1.1 直接开平方法
1.会把一元二次方程降次转化为两个一元一次方程.
2.运用开平方法解形如x2=p或(x+n)2=p(p≥0)的方程.
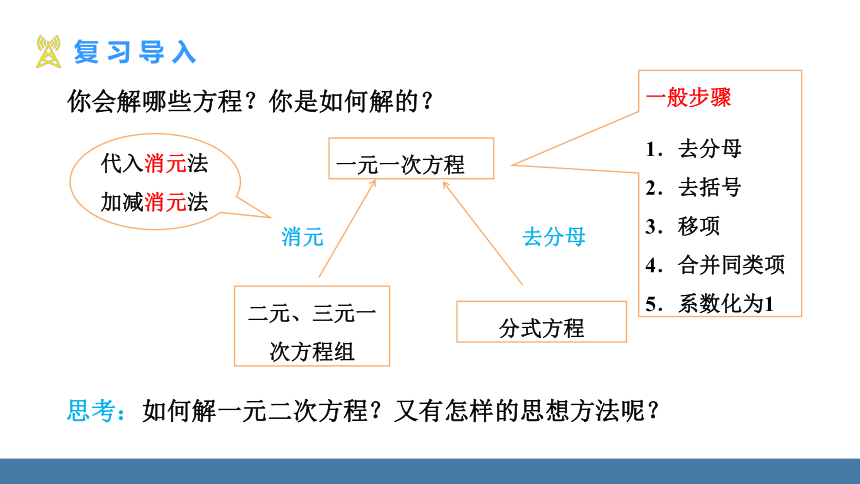
你会解哪些方程?你是如何解的?
二元、三元一次方程组
一元一次方程
分式方程
消元
去分母
思考:如何解一元二次方程?又有怎样的思想方法呢?
一般步骤
1.去分母
2.去括号
3.移项
4.合并同类项
5.系数化为1
代入消元法
加减消元法
问题 一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
直接开平方法解形如x2=p(p≥0)的方程
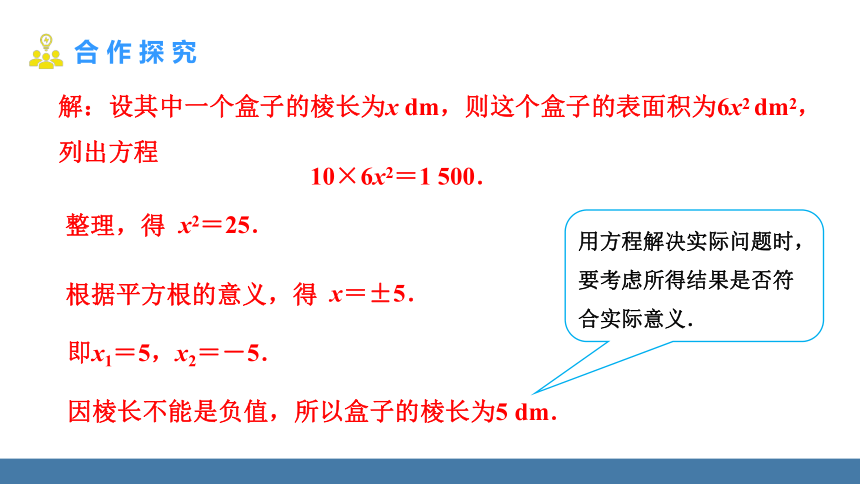
解:设其中一个盒子的棱长为x dm,则这个盒子的表面积为6x2 dm2,列出方程
整理,得
x2=25.
根据平方根的意义,得
即x1=5,x2=-5.
因棱长不能是负值,所以盒子的棱长为5 dm.
x=±5.
用方程解决实际问题时,要考虑所得结果是否符合实际意义.
10×6x2=1 500.
(2)当p=0时,方程(Ⅰ)有两个相等的实数根x1=x2=0;
(3)当p<0时,因为对任意实数x,都有x2≥0,所以方程(Ⅰ)无实数根.
一般地,对于方程x2=p,(Ⅰ)
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的实数根
根据平方根的意义,直接用开平方的方法求一元二次方程的根的方法叫直接开平方法.
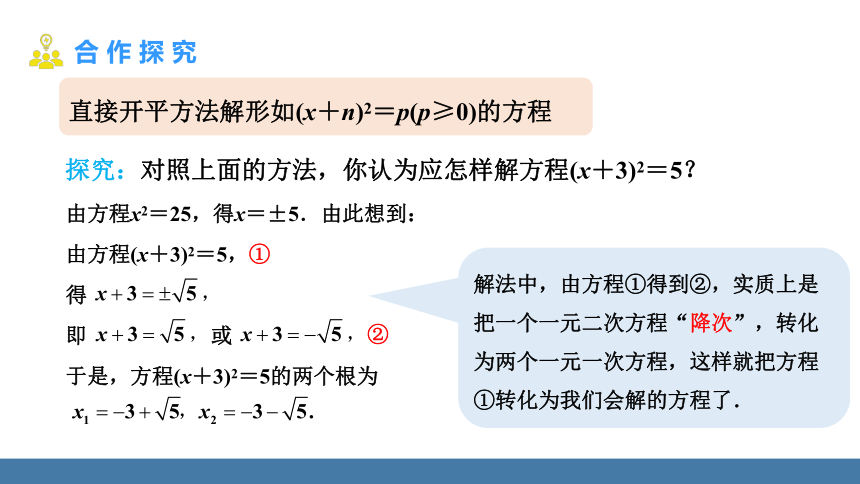
直接开平方法解形如(x+n)2=p(p≥0)的方程
探究:对照上面的方法,你认为应怎样解方程(x+3)2=5?
由方程x2=25,得x=±5.由此想到:
由方程(x+3)2=5,①
得
即 或
②
于是,方程(x+3)2=5的两个根为
解法中,由方程①得到②,实质上是把一个一元二次方程“降次”,转化为两个一元一次方程,这样就把方程①转化为我们会解的方程了.
直接开平方法解一元二次方程的“三步法”
开方
求解
变形
将方程化为含未知数的完全平方式=非负常数的形式;
利用平方根的定义,将方程转化为两个一元一次方程;
解一元一次方程,得出方程的根.
例1 解下列方程:
(2)36x2-1=0.
(1)2x2=8;
解:(1)二次项系数化为1,得x2=4.
开平方,得x=±2.
即 x1=2,x2=-2.
解:(2)移项,得36x2=1.
即 .
二次项系数化为1,得x2= .
开平方,得x=± .
例1 解下列方程:
(2)36x2-1=0.
(1)2x2=8;
例2 解下列方程:
(1)(x+5)2=25;
解:(1)直接开平方,得x+5=±5,
即x+5=5或x+5=-5.
所以x1=0,x2=-10.
(2)4(x-3)2-32=0.
(2)4(x-3)2-32=0.
解:(2)移项,得4(x-3)2=32.
二次项系数化为1,得(x-3)2=8.
直接开平方,得x-3= .
即 或
一移
二化
三开
四解
五写
用直接开平方法解一元二次方程的步骤
所以 , .
1.一元二次方程(x+6)2=16可转化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A.x-6=-4 B.x-6=4
C.x+6=4 D.x+6=-4
D
C.4(x-1)2=9,解方程,得4(x-1)=±3,x1= ,x2=
D.(2x+3)2=25,解方程,得2x+3=±5,x1=1,x2=-4
2.下列解方程的过程中,正确的是( )
A.x2=-2,解方程,得x=±
B.(x-2)2=4,解方程,得x-2=2,x=4
D
(1)方程x2=0.25的根是___________________.
(2)方程2x2=18的根是________________.
(3)方程(2x-1)2=9的根是_______________.
x1=0.5,x2=-0.5
x1=3,x2=-3
x1=2,x2=-1
3.填空:
4.解下列方程:
(1)x2-81=0; (2)2x2=50; (3)(x+1)2=4.
解:(1)x1=9,x2=-9.
(2)x1=5,x2=-5.
(3)x1=1,x2=-3.
直接开平方法
概念
步骤
基本思路
利用平方根的定义求方程的根的方法
关键要把方程化成x2=p(p≥0)或
(x+n)2=p(p≥0)的形式
一元二次方程
两个一元一次方程
降次
直接开平方法
21.2.1.1 直接开平方法
1.会把一元二次方程降次转化为两个一元一次方程.
2.运用开平方法解形如x2=p或(x+n)2=p(p≥0)的方程.
你会解哪些方程?你是如何解的?
二元、三元一次方程组
一元一次方程
分式方程
消元
去分母
思考:如何解一元二次方程?又有怎样的思想方法呢?
一般步骤
1.去分母
2.去括号
3.移项
4.合并同类项
5.系数化为1
代入消元法
加减消元法
问题 一桶油漆可刷的面积为1 500 dm2,李林用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
直接开平方法解形如x2=p(p≥0)的方程
解:设其中一个盒子的棱长为x dm,则这个盒子的表面积为6x2 dm2,列出方程
整理,得
x2=25.
根据平方根的意义,得
即x1=5,x2=-5.
因棱长不能是负值,所以盒子的棱长为5 dm.
x=±5.
用方程解决实际问题时,要考虑所得结果是否符合实际意义.
10×6x2=1 500.
(2)当p=0时,方程(Ⅰ)有两个相等的实数根x1=x2=0;
(3)当p<0时,因为对任意实数x,都有x2≥0,所以方程(Ⅰ)无实数根.
一般地,对于方程x2=p,(Ⅰ)
(1)当p>0时,根据平方根的意义,方程(Ⅰ)有两个不等的实数根
根据平方根的意义,直接用开平方的方法求一元二次方程的根的方法叫直接开平方法.
直接开平方法解形如(x+n)2=p(p≥0)的方程
探究:对照上面的方法,你认为应怎样解方程(x+3)2=5?
由方程x2=25,得x=±5.由此想到:
由方程(x+3)2=5,①
得
即 或
②
于是,方程(x+3)2=5的两个根为
解法中,由方程①得到②,实质上是把一个一元二次方程“降次”,转化为两个一元一次方程,这样就把方程①转化为我们会解的方程了.
直接开平方法解一元二次方程的“三步法”
开方
求解
变形
将方程化为含未知数的完全平方式=非负常数的形式;
利用平方根的定义,将方程转化为两个一元一次方程;
解一元一次方程,得出方程的根.
例1 解下列方程:
(2)36x2-1=0.
(1)2x2=8;
解:(1)二次项系数化为1,得x2=4.
开平方,得x=±2.
即 x1=2,x2=-2.
解:(2)移项,得36x2=1.
即 .
二次项系数化为1,得x2= .
开平方,得x=± .
例1 解下列方程:
(2)36x2-1=0.
(1)2x2=8;
例2 解下列方程:
(1)(x+5)2=25;
解:(1)直接开平方,得x+5=±5,
即x+5=5或x+5=-5.
所以x1=0,x2=-10.
(2)4(x-3)2-32=0.
(2)4(x-3)2-32=0.
解:(2)移项,得4(x-3)2=32.
二次项系数化为1,得(x-3)2=8.
直接开平方,得x-3= .
即 或
一移
二化
三开
四解
五写
用直接开平方法解一元二次方程的步骤
所以 , .
1.一元二次方程(x+6)2=16可转化为两个一元一次方程,其中一个一元一次方程是x+6=4,则另一个一元一次方程是( )
A.x-6=-4 B.x-6=4
C.x+6=4 D.x+6=-4
D
C.4(x-1)2=9,解方程,得4(x-1)=±3,x1= ,x2=
D.(2x+3)2=25,解方程,得2x+3=±5,x1=1,x2=-4
2.下列解方程的过程中,正确的是( )
A.x2=-2,解方程,得x=±
B.(x-2)2=4,解方程,得x-2=2,x=4
D
(1)方程x2=0.25的根是___________________.
(2)方程2x2=18的根是________________.
(3)方程(2x-1)2=9的根是_______________.
x1=0.5,x2=-0.5
x1=3,x2=-3
x1=2,x2=-1
3.填空:
4.解下列方程:
(1)x2-81=0; (2)2x2=50; (3)(x+1)2=4.
解:(1)x1=9,x2=-9.
(2)x1=5,x2=-5.
(3)x1=1,x2=-3.
直接开平方法
概念
步骤
基本思路
利用平方根的定义求方程的根的方法
关键要把方程化成x2=p(p≥0)或
(x+n)2=p(p≥0)的形式
一元二次方程
两个一元一次方程
降次
直接开平方法
同课章节目录
