21.2.4 一元二次方程的根与系数的关系 课件(共20张PPT)
文档属性
| 名称 | 21.2.4 一元二次方程的根与系数的关系 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:02:50 | ||
图片预览








文档简介
(共20张PPT)
*21.2.4 一元二次方程的根与系数的关系
1.探索一元二次方程的根与系数的关系.
2.不解方程,利用一元二次方程的根与系数的关系解决问题.
(1)x2+3x-4=0; (2)x2-5x+6=0; (3)2x2+3x+1=0.
一元二次方程 两根
x1 x2 x2+3x-4=0
x2-5x+6=0
2x2+3x+1=0
-4
1
2
3
-1
-3
-4
5
6
将二次项系数化为1
方程的两根x1和x2与系数a,b,c有什么关系?
解下列方程并完成填空:
x1+x2=?
x1·x2=?
(1)一元二次方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?若将此方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
方程x2+px+q=0的两根x1,x2满足上面两个关系式
(x-x1)(x-x2)=0
x2-(x1+x2)x+x1·x2=0
x2+px+q=0
x1+x2=-p,x1·x2=q
(2)通过前面的表格猜想,如果一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1,x2,那么,你可以发现什么结论?
注:b2-4ac≥0
↗
满足上述关系的前提条件
b2-4ac≥0.
如果ax2+bx+c=0(a≠0)的两个根为x1,x2,那么
一元二次方程的根与系数的关系
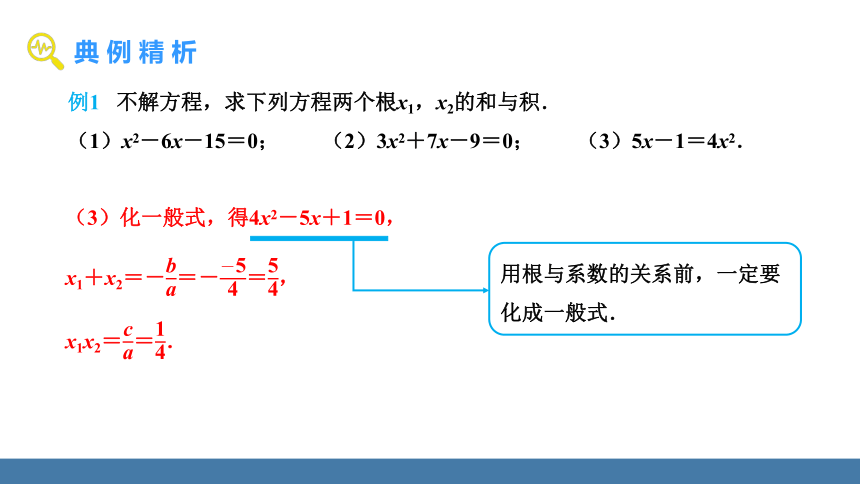
例1 不解方程,求下列方程两个根x1,x2的和与积.
(1)x2-6x-15=0; (2)3x2+7x-9=0; (3)5x-1=4x2.
注意公式自身的符号及系数的符号.
(2)x1+x2=-=-,
x1x2===-3.
解:(1)x1+x2=-(-6)=6,
x1x2=-15.
(3)化一般式,得4x2-5x+1=0,
用根与系数的关系前,一定要化成一般式.
x1+x2=-=-=,
x1x2==.
例1 不解方程,求下列方程两个根x1,x2的和与积.
(1)x2-6x-15=0; (2)3x2+7x-9=0; (3)5x-1=4x2.
与一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2有关的几个代数式的变形
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
1. ;
2. ;
3. ;
4. ;
5. ;
6. .
例2 已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则的值是( )
A. B. C. D.
A
∴.
解析:∵a2-6a+4=0和b2-6b+4=0两个等式的形式相同,且a≠b,
∴a,b可以看成是方程x2-6x+4=0的两个根,∴a+b=6,ab=4,
解:设方程的两根分别为x1,x2,
例3 已知关于x的一元二次方程2x2-mx-2m+1=0的两根的平方和为 ,求m的值.
由已知得
∵ ,∴ ,
∴ ,解得m1=-11,m2=3.
求解此类问题时,必须将求出的字母的值代回原方程进行检验,看是否满足判别式Δ>0,否则可能会多解.
当m=-11时,方程为2x2+11x+23=0,Δ=121-4×2×23=-63<0,
方程无实数根,不合题意,应舍去;
当m=3时,方程为2x2-3x-5=0,Δ=(-3)2-4×2×(-5)=49>0,
方程有两个不相等的实数根.综上所述,m的值为3.
1.关于x的方程x2+px+q=0的根为x1=1+ ,x2=1- ,则p=______,q=______.
-2
-1
-7
2.已知方程5x2+kx-6=0的一根是2,则另一根是______,k=______.
3.求下列方程的两根x1,x2的和与积.
(1)x2-3x+2=0; (2)x2+x=5x+6
解:(1)x1+x2=3,
x1x2=2.
(2)化简得x2-4x-6=0,
则x1+x2=4,x1x2=-6.
4.已知两个数的和为8,积为9.75,求这两个数.
解:设其中一个数为x,则另一个数为8-x.
根据题意,得x(8-x)=9.75,
整理,得x2-8x+9.75=0.
解得x1=6.5,x2=1.5.
当x=6.5时,8-x=1.5;当x=1.5时,8-x=6.5.
∴这两个数是6.5和1.5.
(1) ; (2) .
5.x1,x2是方程x2-5x-7=0的两根,不解方程求下列各式的值.
解:∵x1,x2是方程x2-5x-7=0的两根,
则x1+x2=5,x1x2=-7.
(1) .
(1) ; (2) .
5.x1,x2是方程x2-5x-7=0的两根,不解方程求下列各式的值.
解:(2)
6.已知关于x的方程x2-(2m+3)x+m2=0的两根之和等于两根之积,求m的值.
解:设方程x2-(2m+3)x+m2=0的两根为x1,x2.
∴x1+x2=2m+3,x1x2=m2.
根据题意得m2=2m+3,解得m1=3,m2=-1.
当m=3时,原方程为x2-9x+9=0,b2-4ac=45>0,方程有实数根.
当m=-1时,原方程为x2-x+1=0,b2-4ac=-3<0,方程无实数根,此m值舍去.
∴m的值为3.
一元二次方程的根与系数的关系
内容
变形
如果一元二次方程ax2+bx+c=0(a≠0)的两个根分别是x1,x2,
那么
*21.2.4 一元二次方程的根与系数的关系
1.探索一元二次方程的根与系数的关系.
2.不解方程,利用一元二次方程的根与系数的关系解决问题.
(1)x2+3x-4=0; (2)x2-5x+6=0; (3)2x2+3x+1=0.
一元二次方程 两根
x1 x2 x2+3x-4=0
x2-5x+6=0
2x2+3x+1=0
-4
1
2
3
-1
-3
-4
5
6
将二次项系数化为1
方程的两根x1和x2与系数a,b,c有什么关系?
解下列方程并完成填空:
x1+x2=?
x1·x2=?
(1)一元二次方程(x-x1)(x-x2)=0(x1,x2为已知数)的两根是什么?若将此方程化为x2+px+q=0的形式,你能看出x1,x2与p,q之间的关系吗?
方程x2+px+q=0的两根x1,x2满足上面两个关系式
(x-x1)(x-x2)=0
x2-(x1+x2)x+x1·x2=0
x2+px+q=0
x1+x2=-p,x1·x2=q
(2)通过前面的表格猜想,如果一元二次方程ax2+bx+c=0(a≠0)的两根分别是x1,x2,那么,你可以发现什么结论?
注:b2-4ac≥0
↗
满足上述关系的前提条件
b2-4ac≥0.
如果ax2+bx+c=0(a≠0)的两个根为x1,x2,那么
一元二次方程的根与系数的关系
例1 不解方程,求下列方程两个根x1,x2的和与积.
(1)x2-6x-15=0; (2)3x2+7x-9=0; (3)5x-1=4x2.
注意公式自身的符号及系数的符号.
(2)x1+x2=-=-,
x1x2===-3.
解:(1)x1+x2=-(-6)=6,
x1x2=-15.
(3)化一般式,得4x2-5x+1=0,
用根与系数的关系前,一定要化成一般式.
x1+x2=-=-=,
x1x2==.
例1 不解方程,求下列方程两个根x1,x2的和与积.
(1)x2-6x-15=0; (2)3x2+7x-9=0; (3)5x-1=4x2.
与一元二次方程ax2+bx+c=0(a≠0)的两个根x1,x2有关的几个代数式的变形
求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和、两根之积的形式,再整体代入.
1. ;
2. ;
3. ;
4. ;
5. ;
6. .
例2 已知实数a,b分别满足a2-6a+4=0,b2-6b+4=0,且a≠b,则的值是( )
A. B. C. D.
A
∴.
解析:∵a2-6a+4=0和b2-6b+4=0两个等式的形式相同,且a≠b,
∴a,b可以看成是方程x2-6x+4=0的两个根,∴a+b=6,ab=4,
解:设方程的两根分别为x1,x2,
例3 已知关于x的一元二次方程2x2-mx-2m+1=0的两根的平方和为 ,求m的值.
由已知得
∵ ,∴ ,
∴ ,解得m1=-11,m2=3.
求解此类问题时,必须将求出的字母的值代回原方程进行检验,看是否满足判别式Δ>0,否则可能会多解.
当m=-11时,方程为2x2+11x+23=0,Δ=121-4×2×23=-63<0,
方程无实数根,不合题意,应舍去;
当m=3时,方程为2x2-3x-5=0,Δ=(-3)2-4×2×(-5)=49>0,
方程有两个不相等的实数根.综上所述,m的值为3.
1.关于x的方程x2+px+q=0的根为x1=1+ ,x2=1- ,则p=______,q=______.
-2
-1
-7
2.已知方程5x2+kx-6=0的一根是2,则另一根是______,k=______.
3.求下列方程的两根x1,x2的和与积.
(1)x2-3x+2=0; (2)x2+x=5x+6
解:(1)x1+x2=3,
x1x2=2.
(2)化简得x2-4x-6=0,
则x1+x2=4,x1x2=-6.
4.已知两个数的和为8,积为9.75,求这两个数.
解:设其中一个数为x,则另一个数为8-x.
根据题意,得x(8-x)=9.75,
整理,得x2-8x+9.75=0.
解得x1=6.5,x2=1.5.
当x=6.5时,8-x=1.5;当x=1.5时,8-x=6.5.
∴这两个数是6.5和1.5.
(1) ; (2) .
5.x1,x2是方程x2-5x-7=0的两根,不解方程求下列各式的值.
解:∵x1,x2是方程x2-5x-7=0的两根,
则x1+x2=5,x1x2=-7.
(1) .
(1) ; (2) .
5.x1,x2是方程x2-5x-7=0的两根,不解方程求下列各式的值.
解:(2)
6.已知关于x的方程x2-(2m+3)x+m2=0的两根之和等于两根之积,求m的值.
解:设方程x2-(2m+3)x+m2=0的两根为x1,x2.
∴x1+x2=2m+3,x1x2=m2.
根据题意得m2=2m+3,解得m1=3,m2=-1.
当m=3时,原方程为x2-9x+9=0,b2-4ac=45>0,方程有实数根.
当m=-1时,原方程为x2-x+1=0,b2-4ac=-3<0,方程无实数根,此m值舍去.
∴m的值为3.
一元二次方程的根与系数的关系
内容
变形
如果一元二次方程ax2+bx+c=0(a≠0)的两个根分别是x1,x2,
那么
同课章节目录
