22.1.4.2 用待定系数法求二次函数的解析式 课件(共21张PPT)
文档属性
| 名称 | 22.1.4.2 用待定系数法求二次函数的解析式 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 694.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
22.1.4.2 用待定系数法求二次函数的解析式
1.知道给定不共线三点的坐标可以确定一个二次函数.
2.根据不共线的三点,会用待定系数法求二次函数的解析式.
3.根据具体问题的特征,能选择不同的方法确定二次函数的解析式.
1.求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法
(1)设:设解析式;
(2)代:坐标代入;
(3)解:解方程(组);
(4)还原:写解析式.
2.二次函数解析式:
顶点式:y=a(x-h)2+k(a≠0),顶点为(h,k).
一般式:y=ax2+bx+c(a≠0).
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.对于二次函数,由几个点的坐标可以确定二次函数的解析式?
已知一个二次函数的图象过点(-1,10),(1,4),
求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组.
解:设所求的二次函数为y=ax2+bx+c.
由已知,得
a-b+c=10,
a+b+c=4,
三个未知数,两个等量关系,这个方程组能解吗?
4a+2b+c=7,
(2,7),
4a+2b+c=7,
①
②
③
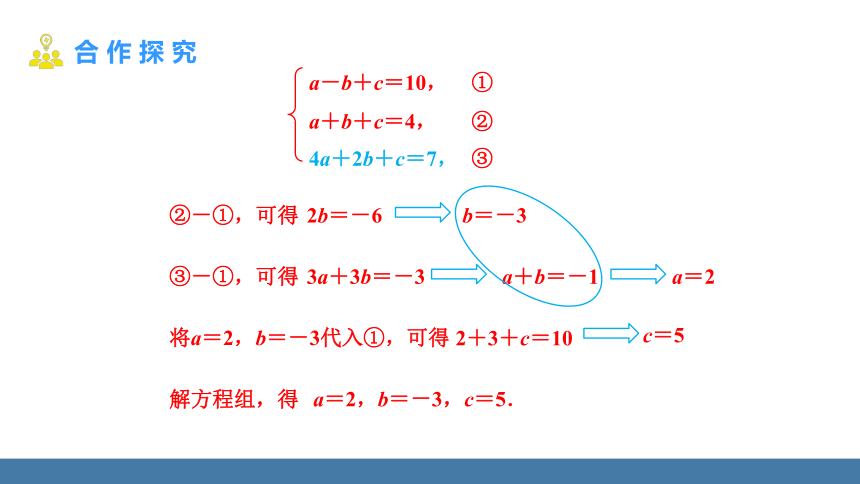
②-①,可得
2b=-6
b=-3
③-①,可得
3a+3b=-3
a+b=-1
a=2
将a=2,b=-3代入①,可得
2+3+c=10
c=5
解方程组,得
a=2,b=-3,c=5.
a-b+c=10,
a+b+c=4,
已知一个二次函数的图象过点(-1,10),(1,4),
求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组.
解:设所求的二次函数为y=ax2+bx+c.
由已知,得
a-b+c=10,
a+b+c=4,
4a+2b+c=7,
(2,7),
解方程组,得
因此,所求二次函数是
a=2,b=-3,c=5.
y=2x2-3x+5.
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值.
由已知条件(如二次函数图象上三个点的坐标)列出关于a,b,c的方程组,然后求出a,b,c,就可以写出二次函数的解析式.
图象顶点为(h,k)的二次函数的解析式是y=a(x-h)2+k,如果顶点坐标已知,那么求解析式的关键是什么?
已知抛物线顶点为(1,-4),且过点(2,-3),求其解析式.
解:∵抛物线顶点为(1,-4),
∴设其解析式为y=a(x-1)2-4.
又∵抛物线过点(2,-3),
则-3=a(2-1)2-4,则a=1.
∴其解析式为y=(x-1)2-4=x2-2x-3.
已知顶点坐标和一点,求二次函数解析式的一般步骤:
第一步:设解析式为y=a(x-h)2+k.
第二步:将已知点坐标代入求a值,得出解析式.
一个二次函数,当自变量x=0时,函数值y=-1,当x=-2与 时,y=0,求这个二次函数的解析式.
两种方法的结果一样吗?两种方法哪一个更简捷?
方法1:设 ,再把x=0,y=-1代入其中,求出a的值.
方法2:设y=ax2+bx+c,由“x=0时,函数值y=-1,当x=-2与 时,y=0”,列方程组求出a,b,c的值.
方法1更简捷.
已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点(两点的纵坐标都为0),与y轴交于点C(0,3),求这个二次函数的解析式.
解:∵图象与x轴交于A(1,0),B(3,0),
∴设函数解析式为y=a(x-1)(x-3).
∵图象过点C(0,3),
∴3=a(0-1)(0-3),解得a=1.
∴二次函数解析式为y=(x-1)(x-3)=x2-4x+3.
交点式法求二次函数的解析式
这种已知道抛物线与x轴的交点,求解析式的方法叫做交点式法.
其步骤是:
(1)设函数解析式是y=a(x-x1)(x-x2);
(2)先把两交点的横坐标x1,x2代入解析式中,得到只含参数a的解析式;
(3)将另一点的坐标代入上步中的解析式,求出a值;
(4)将a用求得的值换掉,写出函数解析式.
用待定系数法求二次函数的解析式的一般步骤:
①设出合适的函数解析式;
②把已知条件代入函数解析式,得到关于待定系数的方程或方程组;
③解方程(组)求出待定系数的值,从而写出函数的解析式.
例1 一个二次函数的图象经过(0,1),(2,4),(3,10)三点,求这个二次函数的解析式.
∴所求的二次函数的解析式是
4a+2b+1=4,
9a+3b+1=10,
c=1,
解得
解:设这个二次函数的解析式是y=ax2+bx+c,
由于这个函数经过点(0,1),(2,4),(3,10),可得
例2 一个二次函数的图象经点(0,1),它的顶点坐标为(8,9),求这个二次函数的解析式.
又∵它的图象经过点(0,1),可得1=a(0-8)2+9,
解得a=,
∴所求的二次函数的解析式是y=(x-8)2+9.
解:∵这个二次函数的图象的顶点坐标为(8,9),
∴设函数解析式为y=a(x-8)2+9.
例3 二次函数图象经过点A(1,0),B(0,-3),对称轴是直线x=2.求出这个二次函数的解析式.
解:∵图象经过点A(1,0),对称轴是直线x=2,
∴图象经过另一点(3,0).
∴设该二次函数的解析式为y=a(x-1)(x-3).
将点(0,-3)代入,得
-3=a(0-1)(0-3),
解得
a=-1.
∴该二次函数的解析式为y=-(x-1)(x-3)=-x2+4x-3.
1.一个二次函数的图象经过(0,0),(-1,-1),(1,9)三点,这个二次函数的解析式是_____________.
y=4x2+5x
∵二次函数的图象经过(0,0),(-1,-1),(1,9)三点,
解析:设这个二次函数的解析式为y=ax2+bx+c,
∴代入得
解得a=4,b=5,c=0,
即二次函数的解析式是y=4x2+5x.
2.过点(2,4),且当x=1时,y有最大值6,则其解析式是__________________.
y=-2(x-1)2+6
解析:根据题意设抛物线解析式为y=a(x-1)2+6,
把(2,4)代入得a+6=4,即a=-2,
则抛物线解析式为y=-2(x-1)2+6.
3.已知抛物线与x轴相交于点A(-1,0),B(1,0),且过点M(0,1),求此函数的解析式.
解:∵点A(-1,0),B(1,0)是图象与x轴的交点,
∴设二次函数的解析式为y=a(x+1)(x-1).
又∵抛物线过点M(0,1),
∴1=a(0+1)(0-1),解得a=-1,
∴所求抛物线的解析式为y=-(x+1)(x-1),
即y=-x2+1.
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
待定系数法
求二次函数解析式
用一般式法:y=ax2+bx+c
用顶点法:y=a(x-h)2+k
用交点式法:
y=a(x-x1)(x-x2)
22.1.4.2 用待定系数法求二次函数的解析式
1.知道给定不共线三点的坐标可以确定一个二次函数.
2.根据不共线的三点,会用待定系数法求二次函数的解析式.
3.根据具体问题的特征,能选择不同的方法确定二次函数的解析式.
1.求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法
(1)设:设解析式;
(2)代:坐标代入;
(3)解:解方程(组);
(4)还原:写解析式.
2.二次函数解析式:
顶点式:y=a(x-h)2+k(a≠0),顶点为(h,k).
一般式:y=ax2+bx+c(a≠0).
我们知道,由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.对于二次函数,由几个点的坐标可以确定二次函数的解析式?
已知一个二次函数的图象过点(-1,10),(1,4),
求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组.
解:设所求的二次函数为y=ax2+bx+c.
由已知,得
a-b+c=10,
a+b+c=4,
三个未知数,两个等量关系,这个方程组能解吗?
4a+2b+c=7,
(2,7),
4a+2b+c=7,
①
②
③
②-①,可得
2b=-6
b=-3
③-①,可得
3a+3b=-3
a+b=-1
a=2
将a=2,b=-3代入①,可得
2+3+c=10
c=5
解方程组,得
a=2,b=-3,c=5.
a-b+c=10,
a+b+c=4,
已知一个二次函数的图象过点(-1,10),(1,4),
求这个函数的解析式.
第一步:设出解析式的形式;
第二步:代入已知点的坐标;
第三步:解方程组.
解:设所求的二次函数为y=ax2+bx+c.
由已知,得
a-b+c=10,
a+b+c=4,
4a+2b+c=7,
(2,7),
解方程组,得
因此,所求二次函数是
a=2,b=-3,c=5.
y=2x2-3x+5.
求二次函数y=ax2+bx+c的解析式,关键是求出待定系数a,b,c的值.
由已知条件(如二次函数图象上三个点的坐标)列出关于a,b,c的方程组,然后求出a,b,c,就可以写出二次函数的解析式.
图象顶点为(h,k)的二次函数的解析式是y=a(x-h)2+k,如果顶点坐标已知,那么求解析式的关键是什么?
已知抛物线顶点为(1,-4),且过点(2,-3),求其解析式.
解:∵抛物线顶点为(1,-4),
∴设其解析式为y=a(x-1)2-4.
又∵抛物线过点(2,-3),
则-3=a(2-1)2-4,则a=1.
∴其解析式为y=(x-1)2-4=x2-2x-3.
已知顶点坐标和一点,求二次函数解析式的一般步骤:
第一步:设解析式为y=a(x-h)2+k.
第二步:将已知点坐标代入求a值,得出解析式.
一个二次函数,当自变量x=0时,函数值y=-1,当x=-2与 时,y=0,求这个二次函数的解析式.
两种方法的结果一样吗?两种方法哪一个更简捷?
方法1:设 ,再把x=0,y=-1代入其中,求出a的值.
方法2:设y=ax2+bx+c,由“x=0时,函数值y=-1,当x=-2与 时,y=0”,列方程组求出a,b,c的值.
方法1更简捷.
已知二次函数y=ax2+bx+c的图象与x轴交于A(1,0),B(3,0)两点(两点的纵坐标都为0),与y轴交于点C(0,3),求这个二次函数的解析式.
解:∵图象与x轴交于A(1,0),B(3,0),
∴设函数解析式为y=a(x-1)(x-3).
∵图象过点C(0,3),
∴3=a(0-1)(0-3),解得a=1.
∴二次函数解析式为y=(x-1)(x-3)=x2-4x+3.
交点式法求二次函数的解析式
这种已知道抛物线与x轴的交点,求解析式的方法叫做交点式法.
其步骤是:
(1)设函数解析式是y=a(x-x1)(x-x2);
(2)先把两交点的横坐标x1,x2代入解析式中,得到只含参数a的解析式;
(3)将另一点的坐标代入上步中的解析式,求出a值;
(4)将a用求得的值换掉,写出函数解析式.
用待定系数法求二次函数的解析式的一般步骤:
①设出合适的函数解析式;
②把已知条件代入函数解析式,得到关于待定系数的方程或方程组;
③解方程(组)求出待定系数的值,从而写出函数的解析式.
例1 一个二次函数的图象经过(0,1),(2,4),(3,10)三点,求这个二次函数的解析式.
∴所求的二次函数的解析式是
4a+2b+1=4,
9a+3b+1=10,
c=1,
解得
解:设这个二次函数的解析式是y=ax2+bx+c,
由于这个函数经过点(0,1),(2,4),(3,10),可得
例2 一个二次函数的图象经点(0,1),它的顶点坐标为(8,9),求这个二次函数的解析式.
又∵它的图象经过点(0,1),可得1=a(0-8)2+9,
解得a=,
∴所求的二次函数的解析式是y=(x-8)2+9.
解:∵这个二次函数的图象的顶点坐标为(8,9),
∴设函数解析式为y=a(x-8)2+9.
例3 二次函数图象经过点A(1,0),B(0,-3),对称轴是直线x=2.求出这个二次函数的解析式.
解:∵图象经过点A(1,0),对称轴是直线x=2,
∴图象经过另一点(3,0).
∴设该二次函数的解析式为y=a(x-1)(x-3).
将点(0,-3)代入,得
-3=a(0-1)(0-3),
解得
a=-1.
∴该二次函数的解析式为y=-(x-1)(x-3)=-x2+4x-3.
1.一个二次函数的图象经过(0,0),(-1,-1),(1,9)三点,这个二次函数的解析式是_____________.
y=4x2+5x
∵二次函数的图象经过(0,0),(-1,-1),(1,9)三点,
解析:设这个二次函数的解析式为y=ax2+bx+c,
∴代入得
解得a=4,b=5,c=0,
即二次函数的解析式是y=4x2+5x.
2.过点(2,4),且当x=1时,y有最大值6,则其解析式是__________________.
y=-2(x-1)2+6
解析:根据题意设抛物线解析式为y=a(x-1)2+6,
把(2,4)代入得a+6=4,即a=-2,
则抛物线解析式为y=-2(x-1)2+6.
3.已知抛物线与x轴相交于点A(-1,0),B(1,0),且过点M(0,1),求此函数的解析式.
解:∵点A(-1,0),B(1,0)是图象与x轴的交点,
∴设二次函数的解析式为y=a(x+1)(x-1).
又∵抛物线过点M(0,1),
∴1=a(0+1)(0-1),解得a=-1,
∴所求抛物线的解析式为y=-(x+1)(x-1),
即y=-x2+1.
①已知三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
已知条件
所选方法
待定系数法
求二次函数解析式
用一般式法:y=ax2+bx+c
用顶点法:y=a(x-h)2+k
用交点式法:
y=a(x-x1)(x-x2)
同课章节目录
