22.2.2 二次函数y=ax?+bx+c的图象与x轴交点情况的探究 课件(共21张PPT)
文档属性
| 名称 | 22.2.2 二次函数y=ax?+bx+c的图象与x轴交点情况的探究 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1008.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
22.2.2 二次函数 y=ax +bx+c 的图象与 x 轴交点情况的探究
1.能从二次函数与一元二次方程的关系中总结出二次函数与x轴交点的个数与一元二次方程根的个数之间的关系.
2.会用一元二次方程解决二次函数图象与x轴的交点问题.
3.能够利用二次函数的图象求一元二次方程的近似解.
x=2
(1)一次函数y=x+2的图象与x轴的交点为( ),
一元一次方程x+2=0的根为____________.
(2)一次函数y=-3x+6的图象与x轴的交点为( ),
一元一次方程-3x+6=0的根为________.
x=-2
-2,0
观察发现:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
2,0
交点横坐标=方程的根
二次函数的图象与x轴的交点呢?
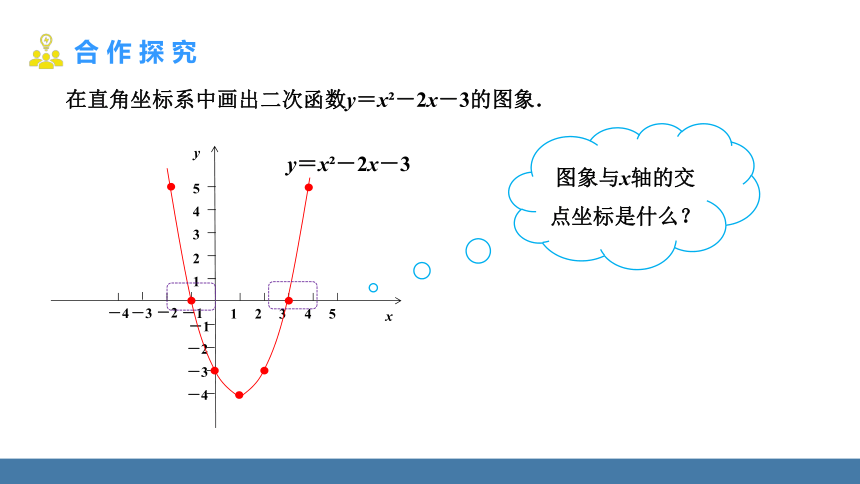
在直角坐标系中画出二次函数y=x -2x-3的图象.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
图象与x轴的交点坐标是什么?
y=x -2x-3
二次函数图象与x轴的交点
坐标是(-1,0),(3,0).
一元二次方程x2-2x-3=0的两根是
x1=-1,x2=3.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=x -2x-3
发现
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根;
(2)二次函数的图象与x轴交点问题可以转化为一元二次方程去解决.
二次函数图象与x轴的交点
坐标是(-1,0),(3,0).
一元二次方程x2-2x-3=0的两根是
x1=-1,x2=3.
例1 求抛物线y=x2+4x-5与x轴的交点坐标.
若一元二次方程ax2+bx+c=0的两个根是x1,x2,则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是( ),( ).
x1,0
x2,0
解:令y=0,
则x2+4x-5=0,
解得x1=-5,x2=1,
∴交点坐标为 (-5,0),(1,0).
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
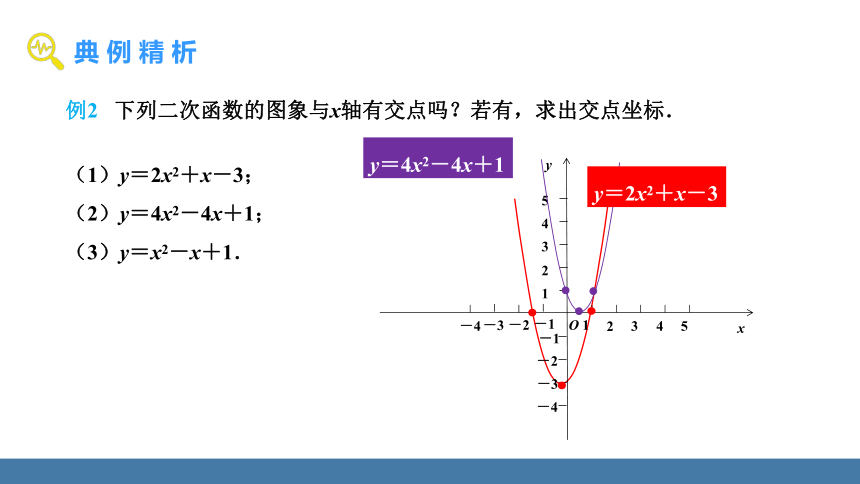
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
O
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
O
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
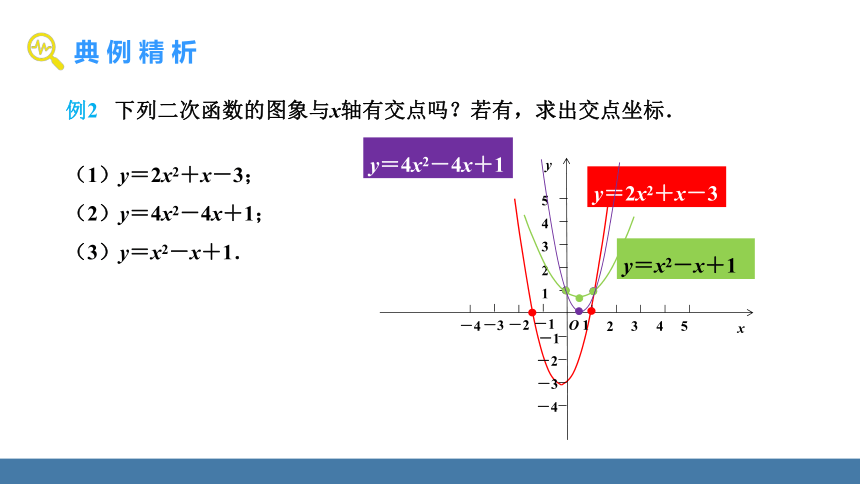
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
两个交点,
坐标:(-,0),(1,0)
无交点
一个交点,
坐标:(,0)
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
O
如何根据二次函数与x轴的交点个数,判断一元二次方程的根的情况?
二次函数与x轴交点个数 一元二次方程根的情况
2个
1个
0个
两个不相等实数根
两个相等
实数根
无实数根
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
O
由?决定
b -4ac的符号
<0
=0
>0
如何根据二次函数与x轴的交点个数,判断一元二次方程的根的情况?
二次函数与x轴交点个数 一元二次方程根的情况
2个
1个
0个
两个不相等实数根
两个相等
实数根
无实数根
二次函数 y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0 的根 一元二次方程
ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的
实数根
没有交点
没有实数根
b2-4ac>0
b2-4ac=0
b2-4ac<0
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
由题意得:
分析:当二次函数y=ax2+bx+c给定y的值时,则可将二次函数转化为一元二次方程.
二次函数y=-x +2x-3的函数值为-8时,所对应的点的横坐标即为方程-x +2x-3=-8的解,故可通过画出函数图象来估算方程的近似解.
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
解:画出函数y=-x +2x-3的图象.
1
2
3
x
-1
-2
-3
-4
-5
y
1
O
-1
-2
4
-6
-7
-8
y=-x +2x-3
根据图象可知,方程-x +2x-3=-8的根是抛物线y=-x +2x-3与直线x=-8的交点的横坐标.
左交点的横坐标在-2到-1之间,
右交点的横坐标在3到4之间.
使用计算器通过不断缩小交点横坐标的范围,来估算方程的解:
左交点 右交点 x -1.3 -1.4 -1.5 … 3.3 3.4 3.5 …
y
-7.29
-7.29
-7.76
-7.76
-8.25
-8.25
…
…
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
观察表格中数据,可得结论:x=-1.4和x=3.4是方程的两个近似根,即x1≈-1.4,x2≈3.4.
一元二次方程ax2+bx+c=m的根实际上是抛物线y=ax2+bx+c与直线y=m的交点的横坐标.
用图象法求一元二次方程的近似根的步骤:
(1)画出函数的图象,并由图象确定方程根的个数;
(2)由图象交点位置确定横坐标的范围;
(3)估计方程的近似根.
1.二次函数y=x2+x-6的图象与x轴交点的横坐标是( )
A.2和-3 B.-2和3
C.2和3 D.-2和3
解析:令x2+x-6=0,解得x1=-3,x2=2,
所以交点横坐标为2和-3,
故选A.
A
2.已知二次函数y=x2-2mx+m2+3(m是常数).求证:不论m为何值,该函数的图象与x轴没有公共点.
即不论m为何值,该函数的图象与x轴没有公共点.
证明:令y=0,得0=x2-2mx+m2+3.
∵Δ=(-2m)2-4×1×(m2+3)
=4m2-4m2-12
=-12<0,
∴方程x2-2mx+m2+3=0没有实数解,
3.利用二次函数的图象估计一元二次方程x2-2x-1=0的近似根(精确到0.1).
解:作出二次函数y=x2-2x-1的图象,如图所示.
故一元二次方程x2-2x-1=0的近似根是x1≈-0.4(或-0.5),x2≈2.4(或2.5).
O
y=x2-2x-1
由图象可知方程有两个根,一个在-1和0之间,另一个在2和3之间.
先求-1和0之间的根.当x=-0.4时,y=-0.04;当x=-0.5时,y=0.25;
因此,x=-0.4(或x=-0.5)是方程的一个近似根,
同理,x=2.4(或x=2.5)是方程的另一个近似根.
画图象
当y=0时
二次函数
一元二次方程
方程根的情况
两个不相等的实数根
两个相等的实数根
没有实数根
抛物线与x轴的公共点情况
两个公共点
一个公共点
没有公共点
Δ>0
Δ=0
Δ<0
解方程
22.2.2 二次函数 y=ax +bx+c 的图象与 x 轴交点情况的探究
1.能从二次函数与一元二次方程的关系中总结出二次函数与x轴交点的个数与一元二次方程根的个数之间的关系.
2.会用一元二次方程解决二次函数图象与x轴的交点问题.
3.能够利用二次函数的图象求一元二次方程的近似解.
x=2
(1)一次函数y=x+2的图象与x轴的交点为( ),
一元一次方程x+2=0的根为____________.
(2)一次函数y=-3x+6的图象与x轴的交点为( ),
一元一次方程-3x+6=0的根为________.
x=-2
-2,0
观察发现:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
2,0
交点横坐标=方程的根
二次函数的图象与x轴的交点呢?
在直角坐标系中画出二次函数y=x -2x-3的图象.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
图象与x轴的交点坐标是什么?
y=x -2x-3
二次函数图象与x轴的交点
坐标是(-1,0),(3,0).
一元二次方程x2-2x-3=0的两根是
x1=-1,x2=3.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=x -2x-3
发现
(1)二次函数y=ax2+bx+c的图象与x轴的交点的横坐标就是当y=0时一元二次方程ax2+bx+c=0的根;
(2)二次函数的图象与x轴交点问题可以转化为一元二次方程去解决.
二次函数图象与x轴的交点
坐标是(-1,0),(3,0).
一元二次方程x2-2x-3=0的两根是
x1=-1,x2=3.
例1 求抛物线y=x2+4x-5与x轴的交点坐标.
若一元二次方程ax2+bx+c=0的两个根是x1,x2,则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是( ),( ).
x1,0
x2,0
解:令y=0,
则x2+4x-5=0,
解得x1=-5,x2=1,
∴交点坐标为 (-5,0),(1,0).
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
O
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
O
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
两个交点,
坐标:(-,0),(1,0)
无交点
一个交点,
坐标:(,0)
例2 下列二次函数的图象与x轴有交点吗?若有,求出交点坐标.
(1)y=2x2+x-3;
(2)y=4x2-4x+1;
(3)y=x2-x+1.
O
如何根据二次函数与x轴的交点个数,判断一元二次方程的根的情况?
二次函数与x轴交点个数 一元二次方程根的情况
2个
1个
0个
两个不相等实数根
两个相等
实数根
无实数根
-1
-1
-2
-3
-4
-2
-3
-4
1
2
3
4
5
1
2
3
4
5
y
x
y=2x2+x-3
y=4x2-4x+1
y=x2-x+1
O
由?决定
b -4ac的符号
<0
=0
>0
如何根据二次函数与x轴的交点个数,判断一元二次方程的根的情况?
二次函数与x轴交点个数 一元二次方程根的情况
2个
1个
0个
两个不相等实数根
两个相等
实数根
无实数根
二次函数 y=ax2+bx+c的图象和x轴交点 一元二次方程 ax2+bx+c=0 的根 一元二次方程
ax2+bx+c=0根的判别式Δ=b2-4ac
有两个交点
有两个不相等的实数根
只有一个交点
有两个相等的
实数根
没有交点
没有实数根
b2-4ac>0
b2-4ac=0
b2-4ac<0
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
由题意得:
分析:当二次函数y=ax2+bx+c给定y的值时,则可将二次函数转化为一元二次方程.
二次函数y=-x +2x-3的函数值为-8时,所对应的点的横坐标即为方程-x +2x-3=-8的解,故可通过画出函数图象来估算方程的近似解.
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
解:画出函数y=-x +2x-3的图象.
1
2
3
x
-1
-2
-3
-4
-5
y
1
O
-1
-2
4
-6
-7
-8
y=-x +2x-3
根据图象可知,方程-x +2x-3=-8的根是抛物线y=-x +2x-3与直线x=-8的交点的横坐标.
左交点的横坐标在-2到-1之间,
右交点的横坐标在3到4之间.
使用计算器通过不断缩小交点横坐标的范围,来估算方程的解:
左交点 右交点 x -1.3 -1.4 -1.5 … 3.3 3.4 3.5 …
y
-7.29
-7.29
-7.76
-7.76
-8.25
-8.25
…
…
例3 利用函数y=-x +2x-3的图象,求方程-x +2x-3=-8的近似解(结果保留小数点后一位).
观察表格中数据,可得结论:x=-1.4和x=3.4是方程的两个近似根,即x1≈-1.4,x2≈3.4.
一元二次方程ax2+bx+c=m的根实际上是抛物线y=ax2+bx+c与直线y=m的交点的横坐标.
用图象法求一元二次方程的近似根的步骤:
(1)画出函数的图象,并由图象确定方程根的个数;
(2)由图象交点位置确定横坐标的范围;
(3)估计方程的近似根.
1.二次函数y=x2+x-6的图象与x轴交点的横坐标是( )
A.2和-3 B.-2和3
C.2和3 D.-2和3
解析:令x2+x-6=0,解得x1=-3,x2=2,
所以交点横坐标为2和-3,
故选A.
A
2.已知二次函数y=x2-2mx+m2+3(m是常数).求证:不论m为何值,该函数的图象与x轴没有公共点.
即不论m为何值,该函数的图象与x轴没有公共点.
证明:令y=0,得0=x2-2mx+m2+3.
∵Δ=(-2m)2-4×1×(m2+3)
=4m2-4m2-12
=-12<0,
∴方程x2-2mx+m2+3=0没有实数解,
3.利用二次函数的图象估计一元二次方程x2-2x-1=0的近似根(精确到0.1).
解:作出二次函数y=x2-2x-1的图象,如图所示.
故一元二次方程x2-2x-1=0的近似根是x1≈-0.4(或-0.5),x2≈2.4(或2.5).
O
y=x2-2x-1
由图象可知方程有两个根,一个在-1和0之间,另一个在2和3之间.
先求-1和0之间的根.当x=-0.4时,y=-0.04;当x=-0.5时,y=0.25;
因此,x=-0.4(或x=-0.5)是方程的一个近似根,
同理,x=2.4(或x=2.5)是方程的另一个近似根.
画图象
当y=0时
二次函数
一元二次方程
方程根的情况
两个不相等的实数根
两个相等的实数根
没有实数根
抛物线与x轴的公共点情况
两个公共点
一个公共点
没有公共点
Δ>0
Δ=0
Δ<0
解方程
同课章节目录
