22.3.1 几何图形面积问题 课件(共18张PPT)
文档属性
| 名称 | 22.3.1 几何图形面积问题 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 705.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 21:41:56 | ||
图片预览




文档简介
(共18张PPT)
22.3.1 几何图形面积问题
1.分析实际问题中变量之间的二次函数关系.
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (2)y=-x2-3x+4.
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);最小值:-9.
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );最大值: .
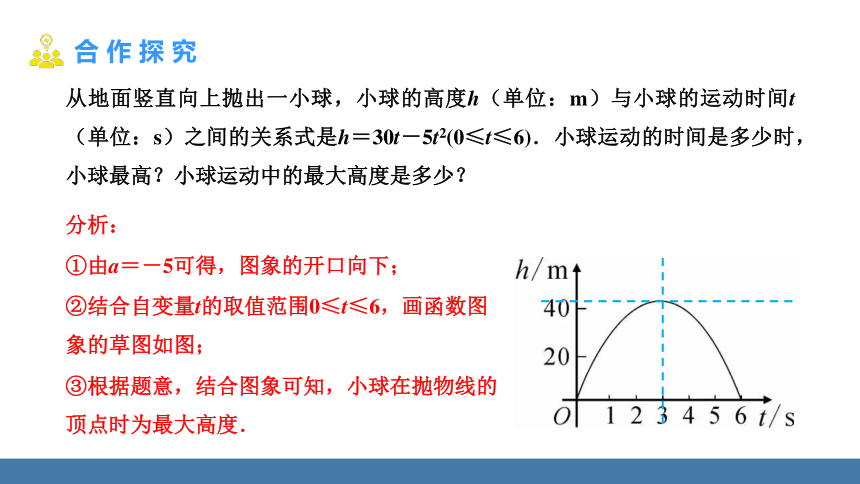
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
分析:
①由a=-5可得,图象的开口向下;
②结合自变量t的取值范围0≤t≤6,画函数图象的草图如图;
③根据题意,结合图象可知,小球在抛物线的顶点时为最大高度.
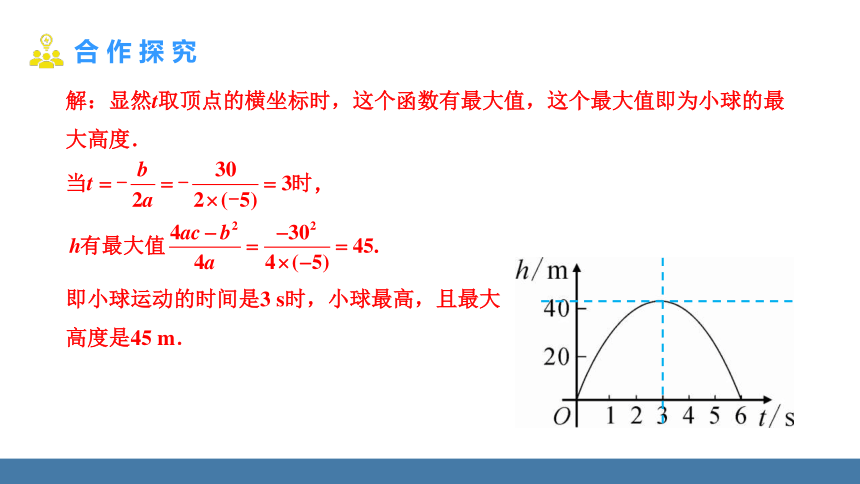
解:显然t取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
即小球运动的时间是3 s时,小球最高,且最大高度是45 m.
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点有最低(高)点,也就是说,当x= 时,二次函数有最小(大)值 .
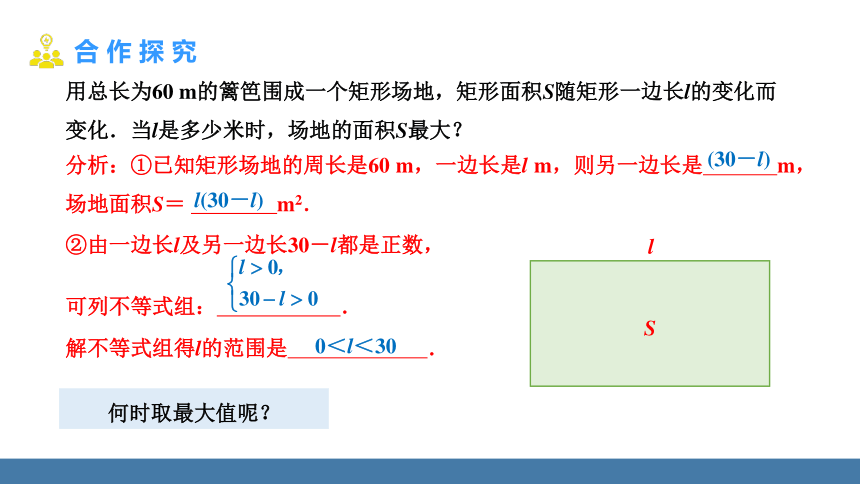
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
l
S
(30-l)
l(30-l)
0<l<30
何时取最大值呢?
分析:①已知矩形场地的周长是60 m,一边长是l m,则另一边长是 m,场地面积S= m2.
②由一边长l及另一边长30-l都是正数,
可列不等式组: .
解不等式组得l的范围是 .
分析:③根据解析式,可以确定这个函数的图象的开口 ,对称轴是 ,顶点坐标是 ,与横轴的交点坐标是 ,与纵轴的交点坐标是 .
向下
直线l=15
(15,225)
(0,0),(30,0)
(0,0)
l
S
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
④根据l的取值范围及③,画出该函数图象的草图.
50
100
S
150
200
250
O
-50
50
l
由图象知:
点 是图象的最高点,即当l= 时,S有最 (选填“大”或“小”)值.
(15,225)
15
大
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
可列方程
S=l(30-l),
即S=-l2+30l
(0<l<30).
即当l是15 m时,场地的面积S最大为225 m2.
l
S
解:矩形场地的周长是60 m,一边长为l m,
所以另一边长为 m.
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
例 如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,这个矩形的长、宽分别为多少时,菜园的面积最大?最大面积是多少?
解:根据题意,设矩形菜园平行于墙的一边长为l m,菜园的面积为S m2,
得(0<l≤18),即S=(0<l≤18).
二次函数S=的对称轴为,
当l<30时,S随l的增大而增大,
因为0<l≤18,所以l=18时,S取得最大值378,
即当矩形的长为21 m,宽是18 m 时,菜园的面积最大,最大面积为378 m2.
注意:实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围进行分析.通过结合实际问题,判断何时在顶点处取最值、何时在端点处取最值.
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,厘清题意.
2.设:找出题中的变量和常量,分析它们之间的关系,设出适当的未知数.
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式.
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题.
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
2.用一条长为40 cm的绳子围成一个面积为a cm2的长方形,a的值不可能为( )
A.20 B.40 C.100 D.120
1.已知一个直角三角形两直角边长之和为20 cm,则这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
D
3.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿AB以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4 cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,那么经过 秒,四边形APQC的面积最小.
A
B
C
P
Q
3
4.如图,四边形的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?
解:设AC=x,四边形ABCD面积为y,
则BD=(10-x).
即当AC,BD的长均为5时,四边形ABCD的面积最大.
几何面积最值问题
一个关键
一个注意
建立函数关系式
依据:常见几何图形的面积公式
最值有时不在顶点处,需要利用函数的增减性来确定
22.3.1 几何图形面积问题
1.分析实际问题中变量之间的二次函数关系.
2.会运用二次函数求实际问题中的最大值或最小值.
3.能应用二次函数的性质解决图形中最大面积问题.
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)y=x2-4x-5; (2)y=-x2-3x+4.
解:(1)开口方向:向上;对称轴:x=2;
顶点坐标:(2,-9);最小值:-9.
(2)开口方向:向下;对称轴:x= ;
顶点坐标:( , );最大值: .
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).小球运动的时间是多少时,小球最高?小球运动中的最大高度是多少?
分析:
①由a=-5可得,图象的开口向下;
②结合自变量t的取值范围0≤t≤6,画函数图象的草图如图;
③根据题意,结合图象可知,小球在抛物线的顶点时为最大高度.
解:显然t取顶点的横坐标时,这个函数有最大值,这个最大值即为小球的最大高度.
即小球运动的时间是3 s时,小球最高,且最大高度是45 m.
一般地,当a>0(a<0)时,抛物线y=ax2+bx+c的顶点有最低(高)点,也就是说,当x= 时,二次函数有最小(大)值 .
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
l
S
(30-l)
l(30-l)
0<l<30
何时取最大值呢?
分析:①已知矩形场地的周长是60 m,一边长是l m,则另一边长是 m,场地面积S= m2.
②由一边长l及另一边长30-l都是正数,
可列不等式组: .
解不等式组得l的范围是 .
分析:③根据解析式,可以确定这个函数的图象的开口 ,对称轴是 ,顶点坐标是 ,与横轴的交点坐标是 ,与纵轴的交点坐标是 .
向下
直线l=15
(15,225)
(0,0),(30,0)
(0,0)
l
S
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
④根据l的取值范围及③,画出该函数图象的草图.
50
100
S
150
200
250
O
-50
50
l
由图象知:
点 是图象的最高点,即当l= 时,S有最 (选填“大”或“小”)值.
(15,225)
15
大
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
可列方程
S=l(30-l),
即S=-l2+30l
(0<l<30).
即当l是15 m时,场地的面积S最大为225 m2.
l
S
解:矩形场地的周长是60 m,一边长为l m,
所以另一边长为 m.
用总长为60 m的篱笆围成一个矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
利用二次函数解决几何图形中的最值问题的要点:
1.根据面积公式、周长公式、勾股定理等建立函数关系式;
2.确定自变量的取值范围;
3.根据开口方向、顶点坐标和自变量的取值范围画草图;
4.根据草图求所得函数在自变量的允许范围内的最大值或最小值.
例 如图,用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,这个矩形的长、宽分别为多少时,菜园的面积最大?最大面积是多少?
解:根据题意,设矩形菜园平行于墙的一边长为l m,菜园的面积为S m2,
得(0<l≤18),即S=(0<l≤18).
二次函数S=的对称轴为,
当l<30时,S随l的增大而增大,
因为0<l≤18,所以l=18时,S取得最大值378,
即当矩形的长为21 m,宽是18 m 时,菜园的面积最大,最大面积为378 m2.
注意:实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围进行分析.通过结合实际问题,判断何时在顶点处取最值、何时在端点处取最值.
用二次函数解决实际问题的一般步骤:
1.审:仔细审题,厘清题意.
2.设:找出题中的变量和常量,分析它们之间的关系,设出适当的未知数.
3.列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,写出二次函数的解析式.
4.解:依据已知条件,借助二次函数的解析式、图象和性质等求解实际问题.
5.检:检验结果,进行合理取舍,得出符合实际意义的结论.
2.用一条长为40 cm的绳子围成一个面积为a cm2的长方形,a的值不可能为( )
A.20 B.40 C.100 D.120
1.已知一个直角三角形两直角边长之和为20 cm,则这个直角三角形的最大面积为( )
A.25 cm2 B.50 cm2 C.100 cm2 D.不确定
B
D
3.如图,在△ABC中,∠B=90°,AB=12 cm,BC=24 cm,动点P从点A开始沿AB以2 cm/s的速度移动(不与点B重合),动点Q从点B开始沿BC以4 cm/s的速度移动(不与点C重合).如果P,Q分别从A,B同时出发,那么经过 秒,四边形APQC的面积最小.
A
B
C
P
Q
3
4.如图,四边形的两条对角线AC,BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形ABCD的面积最大?
解:设AC=x,四边形ABCD面积为y,
则BD=(10-x).
即当AC,BD的长均为5时,四边形ABCD的面积最大.
几何面积最值问题
一个关键
一个注意
建立函数关系式
依据:常见几何图形的面积公式
最值有时不在顶点处,需要利用函数的增减性来确定
同课章节目录
