22.3.3 抛物线型的实际问题 课件(共17张PPT)
文档属性
| 名称 | 22.3.3 抛物线型的实际问题 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 800.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
22.3.3 抛物线型的实际问题
1.能建立合适的直角坐标系,用二次函数的知识解决与抛物线相关的实际问题.
2.进一步巩固二次函数的性质与图象特征.
生活中我们可以看到很多抛物线形的物体或运动轨迹,比如拱桥、喷泉等,还有其他的例子吗?
如图是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.
为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
解:设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-.
这条抛物线表示的二次函数为y=-x2.
当水面下降1 m时,水面的纵坐标为-3.
当y=-3时,-x2=-3,解得x1=,x2=-,
所以当水面下降1 m时,水面宽度为2 m.
水面下降1 m,水面宽度增加(-4) m.
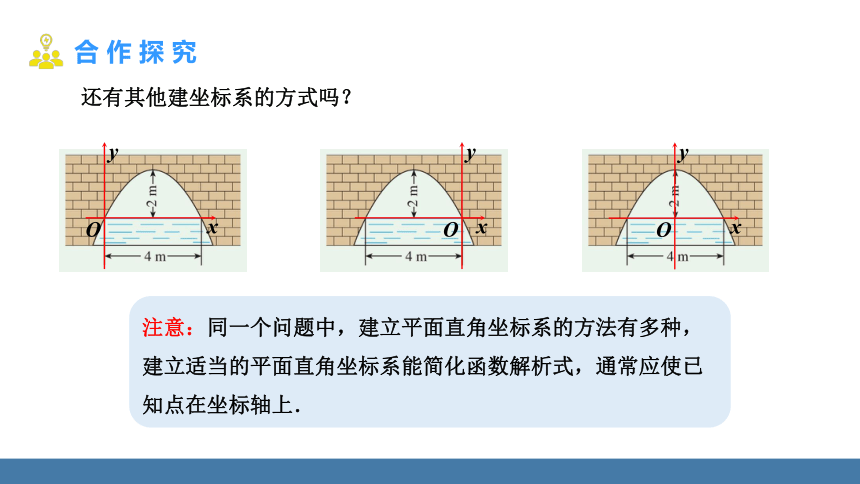
还有其他建坐标系的方式吗?
x
y
O
x
y
O
x
y
O
注意:同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式,通常应使已知点在坐标轴上.
解决形状为抛物线形的实际问题时,一般分为以下四个步骤:
(1)建立适当的平面直角坐标系;
(2)根据条件,把已知的线段长转化为点的坐标;
(3)恰当选用二次函数的解析式形式,用待定系数法求出抛物线的解析式;
(4)利用抛物线解析式求出与问题相关的点的坐标,进而得到实际问题的解.
例1 如图,隧道的截面由抛物线和长方形构成,长方形OABC的长是12 m,宽是4 m,按照图中所示的平面直角坐标系,抛物线可以用y=- x2+2x+c表示.
(1)请写出该抛物线的函数关系式;
解:根据题意得C(0,4),
把C(0,4)代入y=- x2+2x+c得c=4,
所以抛物线解析式为y=-
x2
+2x+4.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
∴这辆货车能安全通过.
∴对称轴为x=6,
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
解:抛物线解析式为y=- x2+2x+4=-
(x-6)2+10,
例2 跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分.一名运动员起跳后,他的飞行路线如图所示,当他的水平距离为15 m时,达到飞行的最高点C处,此时的竖直高度为45 m,他落地时的水平距离(即OA的长)为60 m,求这名运动员起跳时的竖直高度(即OB的长).
∵与x轴交于点A(60,0),
解:设抛物线的解析式为y=a(x-h)2+k,
根据题意得:抛物线的顶点坐标为(15,45),
∴y=a(x-15)2+45.
∴0=a(60-15)2+45,
∴这名运动员起跳时的竖直高度为40米.
解得:a=- .
∴解析式为y=- (x-15)2+45,
令x=0得:y=- (0-15)2+45=40,
∴点B的坐标为(0,40),
例3 如图,施工队要修建一个横断面为抛物线的隧道,OM宽度为16米,其顶点P到OM的距离为8米.
(1)请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
设y=a(x-8)2+8,
x
y
解:如图,以O为原点建立平面直角坐标系,易得抛物线的顶点坐标为(8,8).
将点(0,0)代入上式,得0=64a+8,
解得
故函数的解析式为 (0≤x≤16).
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽3.5米、高5.8米的特种车辆?请通过计算说明.
即允许的最大高度为6米,
解:由题意得车沿着隔离带边沿行驶时,车最左侧与边沿处的距离x=7.5-3.5=4.
当x=4时,y=6,
而5.8<6,故该车辆能通行.但是车顶与隧道间距很小,需小心行驶.
8
16
4
7.5
x
y
1.某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )
A.9.2 m B.9.1 m
C.9 m D.5.1 m
B
2.某涵洞是抛物线形,它的截面如图所示,现测得水平宽度AB=1.6 m,涵洞顶点O到水面的距离为2.4 m,那么在如图所示的直角坐标系中,涵洞所在的抛物线的解析式是 .
y=-3.75x2
A B
3.某幢建筑物,从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,离地面 米,求水流落地点B离墙的距离.
M
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线形问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确地转化为点的坐标;
选择简便的运算方法.
实际问题
数学模型
转化的关键
22.3.3 抛物线型的实际问题
1.能建立合适的直角坐标系,用二次函数的知识解决与抛物线相关的实际问题.
2.进一步巩固二次函数的性质与图象特征.
生活中我们可以看到很多抛物线形的物体或运动轨迹,比如拱桥、喷泉等,还有其他的例子吗?
如图是抛物线形拱桥,当拱顶离水面2 m时,水面宽4 m.水面下降1 m,水面宽度增加多少?
分析:我们知道,二次函数的图象是抛物线,建立适当的坐标系,就可以求出这条抛物线表示的二次函数.
为解题简便,以拋物线的顶点为原点,以抛物线的对称轴为y轴建立直角坐标系(如图).
解:设这条抛物线表示的二次函数为y=ax2.
由抛物线经过点(2,-2),可得-2=a×22,a=-.
这条抛物线表示的二次函数为y=-x2.
当水面下降1 m时,水面的纵坐标为-3.
当y=-3时,-x2=-3,解得x1=,x2=-,
所以当水面下降1 m时,水面宽度为2 m.
水面下降1 m,水面宽度增加(-4) m.
还有其他建坐标系的方式吗?
x
y
O
x
y
O
x
y
O
注意:同一个问题中,建立平面直角坐标系的方法有多种,建立适当的平面直角坐标系能简化函数解析式,通常应使已知点在坐标轴上.
解决形状为抛物线形的实际问题时,一般分为以下四个步骤:
(1)建立适当的平面直角坐标系;
(2)根据条件,把已知的线段长转化为点的坐标;
(3)恰当选用二次函数的解析式形式,用待定系数法求出抛物线的解析式;
(4)利用抛物线解析式求出与问题相关的点的坐标,进而得到实际问题的解.
例1 如图,隧道的截面由抛物线和长方形构成,长方形OABC的长是12 m,宽是4 m,按照图中所示的平面直角坐标系,抛物线可以用y=- x2+2x+c表示.
(1)请写出该抛物线的函数关系式;
解:根据题意得C(0,4),
把C(0,4)代入y=- x2+2x+c得c=4,
所以抛物线解析式为y=-
x2
+2x+4.
(2)一辆货运汽车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
∴这辆货车能安全通过.
∴对称轴为x=6,
由题意得货运汽车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y= >6,
解:抛物线解析式为y=- x2+2x+4=-
(x-6)2+10,
例2 跳台滑雪是冬季奥运会比赛项目之一,运动员起跳后的飞行路线可以看作是抛物线的一部分.一名运动员起跳后,他的飞行路线如图所示,当他的水平距离为15 m时,达到飞行的最高点C处,此时的竖直高度为45 m,他落地时的水平距离(即OA的长)为60 m,求这名运动员起跳时的竖直高度(即OB的长).
∵与x轴交于点A(60,0),
解:设抛物线的解析式为y=a(x-h)2+k,
根据题意得:抛物线的顶点坐标为(15,45),
∴y=a(x-15)2+45.
∴0=a(60-15)2+45,
∴这名运动员起跳时的竖直高度为40米.
解得:a=- .
∴解析式为y=- (x-15)2+45,
令x=0得:y=- (0-15)2+45=40,
∴点B的坐标为(0,40),
例3 如图,施工队要修建一个横断面为抛物线的隧道,OM宽度为16米,其顶点P到OM的距离为8米.
(1)请建立适当的平面直角坐标系,并求出这条抛物线的函数解析式;
设y=a(x-8)2+8,
x
y
解:如图,以O为原点建立平面直角坐标系,易得抛物线的顶点坐标为(8,8).
将点(0,0)代入上式,得0=64a+8,
解得
故函数的解析式为 (0≤x≤16).
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽3.5米、高5.8米的特种车辆?请通过计算说明.
即允许的最大高度为6米,
解:由题意得车沿着隔离带边沿行驶时,车最左侧与边沿处的距离x=7.5-3.5=4.
当x=4时,y=6,
而5.8<6,故该车辆能通行.但是车顶与隧道间距很小,需小心行驶.
8
16
4
7.5
x
y
1.某大学的校门是一抛物线形水泥建筑物(如图所示),大门的地面宽度为8米,两侧距地面4米高处各有一个挂校名横匾用的铁环,两铁环的水平距离为6米,则校门的高为(精确到0.1米,水泥建筑物厚度忽略不计)( )
A.9.2 m B.9.1 m
C.9 m D.5.1 m
B
2.某涵洞是抛物线形,它的截面如图所示,现测得水平宽度AB=1.6 m,涵洞顶点O到水面的距离为2.4 m,那么在如图所示的直角坐标系中,涵洞所在的抛物线的解析式是 .
y=-3.75x2
A B
3.某幢建筑物,从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,离地面 米,求水流落地点B离墙的距离.
M
转化
回归
(二次函数的图象和性质)
拱桥问题
运动中的抛物线形问题
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确地转化为点的坐标;
选择简便的运算方法.
实际问题
数学模型
转化的关键
同课章节目录
