23.1.3 与旋转有关的计算与证明 课件(共19张PPT)

(共19张PPT)
23.1.3　与旋转有关的计算与证明
1.复习旋转及旋转图形的概念及基本性质
2.能综合运用旋转性质解决有关代数，几何类问题．
旋转的性质的应用
一个图形旋转后得到一个新图形.
（1）新旧图形的大小和形状完全_______，只是_______发生改变；
（2）对应线段_______，对应角_______，对应边的夹角为旋转角.
相同
位置
相等
相等
利用以上性质，可以进行相关计算或证明.
1.如图，矩形ABCD绕顶点A旋转后得到矩形AEFG，点B，A，G在同一直线上，试回答下列问题：
(1)旋转角度是多少？
∴∠BAD是旋转角．
∴旋转角度是90°.
解：∵矩形ABCD绕顶点A旋转后得到矩形AEFG，
点B，A，G在同一直线上，
(2)△ACF是什么形状？说明理由．
解：△ACF是等腰直角三角形．理由如下：
∴△ACF是等腰直角三角形．
∵点C绕点A旋转90°到点F，
∴AC＝AF，∠CAF＝90°.
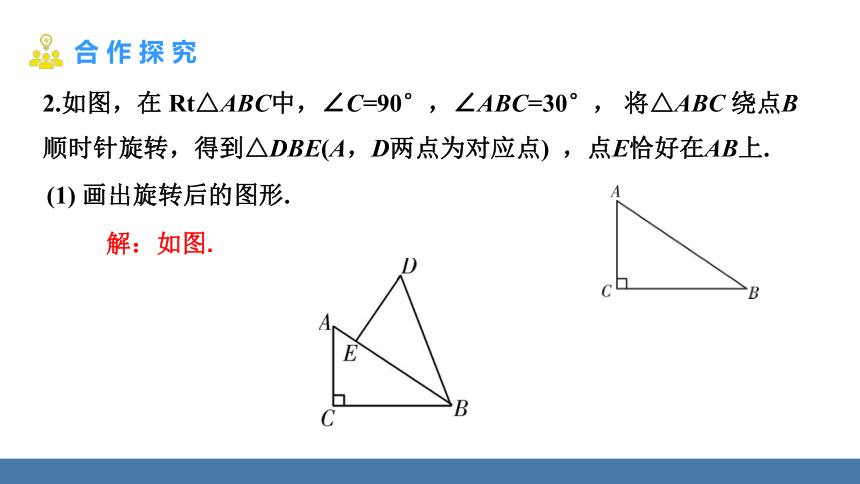
2.如图，在 Rt△ABC中，∠C=90°，∠ABC=30°， 将△ABC 绕点B 顺时针旋转，得到△DBE(A，D两点为对应点) ，，，，，，， ，点E恰好在AB上.
(1) 画出旋转后的图形.
解：如图.
(2) 连接AD ，求∠ADE 的度数.
解：根据题意，
得∠BED=∠C=90°，∠DBE=∠ABC=30°，BD=BA，∴∠ADB=∠DAB=BD=BABDDDLWKDOEWJIOCDNBB×(180°－30°)=75°.
∵∠AED=∠BED=90°，
∴∠ADE=90°－∠DAE=90°－75°=15°.
小结：旋转变换是将已知图形绕某一点旋转，构造出新的图形，可以等量转移图形的相关量，从而将一些分散的条件集中.
3.如图，在四边形ABCD中，∠ABC=∠ADC=45°， 将△BCD绕点C 顺时针旋转一定角度后，点B的对应点恰好与点A重合，得到△ACE.
(1) 判断△ABC的形状，并说明理由.
理由如下：由旋转的性质，得CB=CA，∠CAB=∠CBA=45°，∴∠ACB=90°.
∴△ABC是等腰直角三角形.
解：△ABC是等腰直角三角形.
（2） 若AD=2，CD=3， 请求出四边形ABCDABCDA的对角线BD的长.
.
.
解： 连接 ，由旋转的性质可知 ，
， ， ， .
， .
1.如图，在△ABC中，∠BAC＝120°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD.当点A，D，E在同一条直线上时，下列结论一定正确的是(　 　)
A．∠ABC＝∠ADC 　　　B．CB＝CD
C．DE＋DC＝BC 　　 　 D．AB∥CD
解析：由旋转的性质得出CD＝CA，∠EDC＝∠CAB＝120°.
∵点A，D，E在同一条直线上，
∴∠ADC＝60°.∴△ADC为等边三角形．
∴∠DAC＝60°，∴∠BAD＝60°＝∠ADC，∴AB∥CD.
D
C
3.如图，在△ABC中，点D在AB边上，CB＝CD，将边CA绕点C旋转到CE的位置，使得∠ECA＝∠DCB，连接DE与AC交于点F，且∠B＝70°，∠A＝10°.
(1)求证：AB＝ED；
证明：∵∠ECA＝∠DCB，
∴∠ECA＋∠ACD＝∠DCB＋∠ACD，
即∠ECD＝∠BCA.
由旋转的性质可得CA＝CE.
由SAS可证△BCA≌△DCE.∴AB＝ED.
解：∵△BCA≌△DCE，∴∠CDE＝∠B＝70°，
又CB＝CD，∴∠B＝∠CDB＝70°.
(2)求∠AFE的度数．
∴∠EDA＝180°－∠BDE＝180°－70°×2＝40°.
∴∠AFE＝∠EDA＋∠A＝40°＋10°＝50°.
4.如图，点M，N分别在正方形ABCD的边BC，CD上，且∠MAN＝45°.把△ADN绕点A顺时针旋转90°得到△ABE.
(1)求证：△AEM≌△ANM；
证明：由旋转的性质得△ADN≌△ABE，
∴∠DAN＝∠BAE，AE＝AN.
∵∠DAB＝90°，∠MAN＝45°，
∴∠MAE＝∠BAE＋∠BAM＝∠DAN＋∠BAM＝45°.
∴∠MAE＝∠MAN.
又AM＝AM，∴△AEM≌△ANM(SAS)．
解：设CD＝BC＝x，则CM＝x－3，CN＝x－2.
∵△AEM≌△ANM，∴EM＝MN.
∵BE＝DN，
∴MN＝EM＝BM＋BE＝BM＋DN＝5.
∵∠C＝90°，∴MN2＝CM2＋CN2，
即25＝(x－3)2＋(x－2)2，解得x＝6或x＝－1(舍去)．
∴正方形ABCD的边长为6.
(2)若BM＝3，DN＝2，求正方形ABCD的边长．
旋转的性质的作用：
1.可以用来判断线段或角是否相等.
2.可以用来计算图形的面积、线段的长度或角的大小.
3.可以用来确定旋转中心：因为对应点到旋转中心的距离相等，所以旋转中心在对应点所连线段的垂直平分线上，因此旋转中心是两对对应点所连线段的垂直平分线的交点.