23.2.2 中心对称图形 课件(共17张PPT)
文档属性
| 名称 | 23.2.2 中心对称图形 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
23.2.2 中心对称图形
1. 会识别中心对称图形.
2. 会运用中心对称图形的性质解决实际问题.
3. 理解中心对称与中心对称图形的区别与联系.
思考
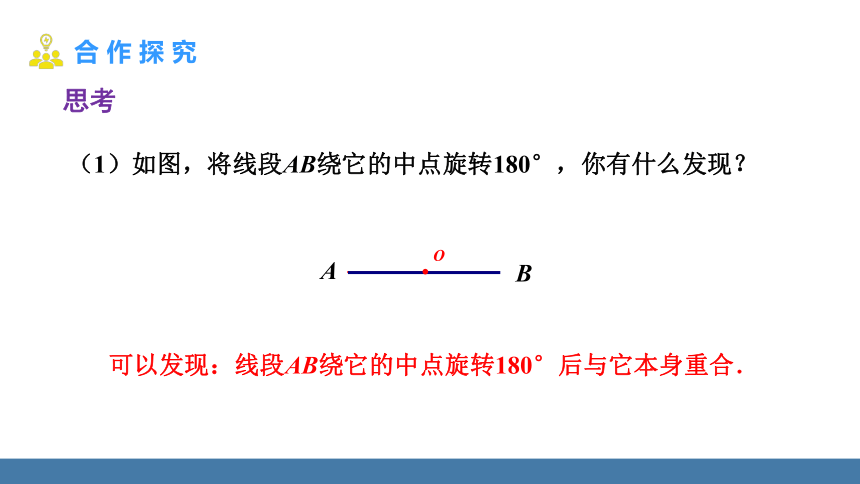
(1)如图,将线段AB绕它的中点旋转180°,你有什么发现?
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
A
B
O
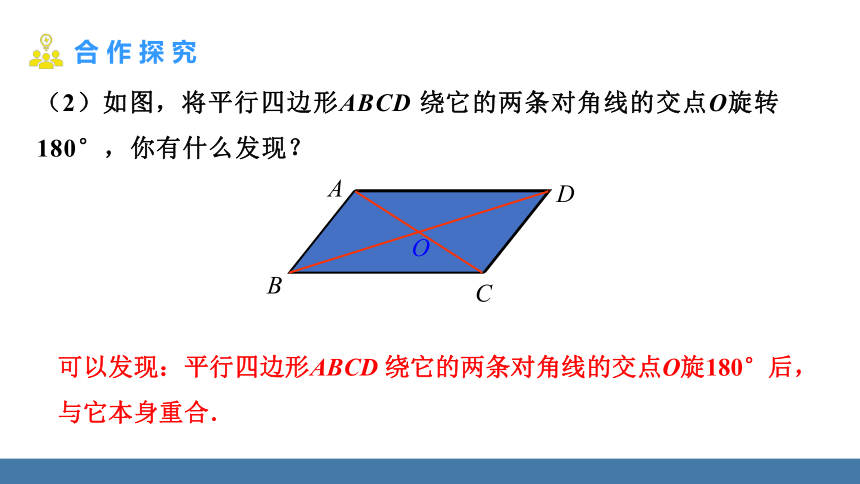
(2)如图,将平行四边形ABCD 绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
可以发现:平行四边形ABCD 绕它的两条对角线的交点O旋180°后,
与它本身重合.
定义:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
1. 中心对称图形的“三要素”:
(1) 对称中心;(2) 旋转180°;(3) 与本身重合.
2. 常见的中心对称图形:线段、平行四边形、矩形、菱形、边数是偶数的正多边形、圆等.
判断中心对称图形的方法
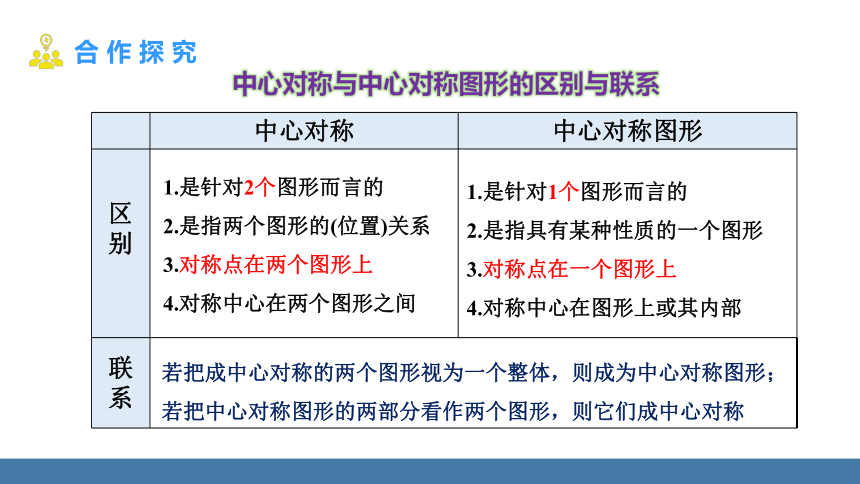
中心对称与中心对称图形的区别与联系
中心对称 中心对称图形
区别
联系 1.是针对2个图形而言的
2.是指两个图形的(位置)关系
3.对称点在两个图形上
4.对称中心在两个图形之间
1.是针对1个图形而言的
2.是指具有某种性质的一个图形
3.对称点在一个图形上
4.对称中心在图形上或其内部
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
探究
A
B
D
C
O
对称中心
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
1. 中心对称图形上的每一对对应点所连线段必经过对称中心,且被对称中心平分;
2. 中心对称图形是指一个图形本身是中心对称的,它反映了一个图形的本质特征,而中心对称是指两个图形关于某一点对称,揭示的是两个全等图形之间的一种位置关系.
3. 过中心对称图形对称中心的直线将图形分成全等的两部分.
中心对称图形的性质
例1 有一块如图所示的钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出分割方法.
分析:过中心对称图形对称中心的直线将图形分成全等的两部分.可以将不规则图形分割成若干规则的中心对称图形,然后再去解题.
解:钢板可看成由上、下两个矩形构成,矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过这两个对称中心作直线可.(画法不唯一)
例2 下列图形中,既是轴对称图形又是中心对称图形的是 ( )
分析:紧扣中心对称图形和轴对称图形的定义进行识别,
掌握轴对称图形和中心对称图形的特征是解题的关键.
例2 下列图形中,既是轴对称图形又是中心对称图形的是 ( )
B
解析:A. 是轴对称图形, 不是中心对称图形,故本选项不合题意;
B. 既是轴对称图形, 又是中心对称图形, 故本选项符合题意;
C. 不是轴对称图形, 是中心对称图形,故本选项不合题意;
D. 不是轴对称图形, 是中心对称图形, 故本选项不合题意.
1.下列美术字中,既是轴对称图形又是中心对称图形的是( )
C
2.有下列图形:①平行四边形;②正方形;③等边三角形;④等腰梯形;⑤菱形;⑥圆;⑦正八边形.其中既是轴对称图形又是中心对称图形的是___________(填序号).
②⑤⑥⑦
3.下图都是中心对称图形,请找到它们的对称中心.
解:如图.
中心对称图形
中心对称图形的有关概念
中心对称图形的性质
中心对称图形的作图
中心对称与中心对称图形的区别与联系
23.2.2 中心对称图形
1. 会识别中心对称图形.
2. 会运用中心对称图形的性质解决实际问题.
3. 理解中心对称与中心对称图形的区别与联系.
思考
(1)如图,将线段AB绕它的中点旋转180°,你有什么发现?
可以发现:线段AB绕它的中点旋转180°后与它本身重合.
A
B
O
(2)如图,将平行四边形ABCD 绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
可以发现:平行四边形ABCD 绕它的两条对角线的交点O旋180°后,
与它本身重合.
定义:把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
1. 中心对称图形的“三要素”:
(1) 对称中心;(2) 旋转180°;(3) 与本身重合.
2. 常见的中心对称图形:线段、平行四边形、矩形、菱形、边数是偶数的正多边形、圆等.
判断中心对称图形的方法
中心对称与中心对称图形的区别与联系
中心对称 中心对称图形
区别
联系 1.是针对2个图形而言的
2.是指两个图形的(位置)关系
3.对称点在两个图形上
4.对称中心在两个图形之间
1.是针对1个图形而言的
2.是指具有某种性质的一个图形
3.对称点在一个图形上
4.对称中心在图形上或其内部
若把成中心对称的两个图形视为一个整体,则成为中心对称图形;若把中心对称图形的两部分看作两个图形,则它们成中心对称
探究
A
B
D
C
O
对称中心
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
1. 中心对称图形上的每一对对应点所连线段必经过对称中心,且被对称中心平分;
2. 中心对称图形是指一个图形本身是中心对称的,它反映了一个图形的本质特征,而中心对称是指两个图形关于某一点对称,揭示的是两个全等图形之间的一种位置关系.
3. 过中心对称图形对称中心的直线将图形分成全等的两部分.
中心对称图形的性质
例1 有一块如图所示的钢板,工人师傅想把它分成面积相等的两部分,请你在图中画出分割方法.
分析:过中心对称图形对称中心的直线将图形分成全等的两部分.可以将不规则图形分割成若干规则的中心对称图形,然后再去解题.
解:钢板可看成由上、下两个矩形构成,矩形是中心对称图形,过对称中心的任一直线把矩形分成全等的两部分,自然平分其面积,而矩形的对称中心是两条对角线的交点,因此,先作出两矩形的对称中心,过这两个对称中心作直线可.(画法不唯一)
例2 下列图形中,既是轴对称图形又是中心对称图形的是 ( )
分析:紧扣中心对称图形和轴对称图形的定义进行识别,
掌握轴对称图形和中心对称图形的特征是解题的关键.
例2 下列图形中,既是轴对称图形又是中心对称图形的是 ( )
B
解析:A. 是轴对称图形, 不是中心对称图形,故本选项不合题意;
B. 既是轴对称图形, 又是中心对称图形, 故本选项符合题意;
C. 不是轴对称图形, 是中心对称图形,故本选项不合题意;
D. 不是轴对称图形, 是中心对称图形, 故本选项不合题意.
1.下列美术字中,既是轴对称图形又是中心对称图形的是( )
C
2.有下列图形:①平行四边形;②正方形;③等边三角形;④等腰梯形;⑤菱形;⑥圆;⑦正八边形.其中既是轴对称图形又是中心对称图形的是___________(填序号).
②⑤⑥⑦
3.下图都是中心对称图形,请找到它们的对称中心.
解:如图.
中心对称图形
中心对称图形的有关概念
中心对称图形的性质
中心对称图形的作图
中心对称与中心对称图形的区别与联系
同课章节目录
