24.1.1 圆 课件(共21张PPT)
文档属性
| 名称 | 24.1.1 圆 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 771.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 21:57:23 | ||
图片预览






文档简介
(共21张PPT)
24.1.1 圆
1.认识圆,理解圆的本质属性.
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.
圆是常见的几何图形,圆形物体在生活中随处可见.圆也是一种美丽的图形,具有独特的对称性,无论从哪个角度看,它都具有同一形状.十五的满月、圆圆的月饼象征着圆满、团圆、和谐.
本节我们将在前面学习的基础上,进一步认识圆,学习与圆有关的性质.
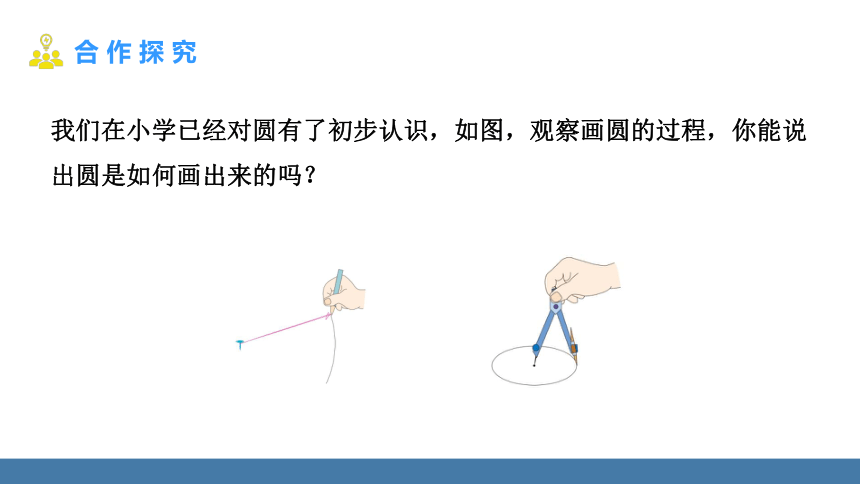
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
·
r
O
A
如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心,线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置;
二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“圆上的点”指圆周上的点.
(1) 圆上各点到定点(圆心O)的距离都等于 .
(2) 到定点的距离等于定长的点都在 .
定长 r
同一个圆上
想一想,从画圆的过程可以看出什么呢?
结论:
圆心为O,半径为 r 的圆可以看成是所有到定点O的距离等于定长 r 的点的集合.
C
A
·
O
B
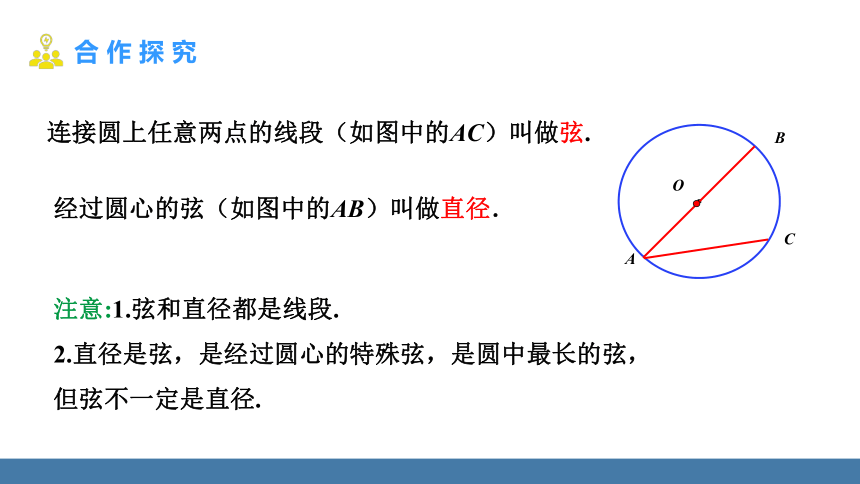
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
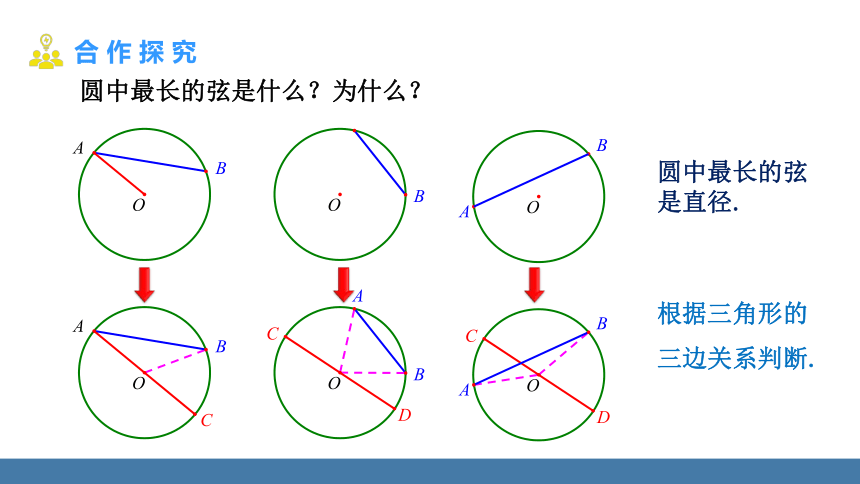
圆中最长的弦是什么?为什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
根据三角形的三边关系判断.
圆中最长的弦
是直径.
·
C
O
A
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧:圆上任意两点间的部分叫做圆弧,简称弧.以A,B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧:小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
B
·
C
O
A
等圆: 能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:等圆是两个半径相等的圆.
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
·
C
O
A
如图,如果弧AB和弧CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
这两条弧不可能完全重合,因为这两条弧弯曲程度不同,“等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或者等圆中.
特别提醒
1.弦与直径的关系:直径是过圆心最长的弦,但弦不一定是直径.
2.弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦是圆上两点间的线段,有无数条;弧是圆上两点间的部分,是曲线,也有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条:一条优弧、一条劣弧或两个半圆.
例1 下列语句中:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有_________ .
解析:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半径相等的两个半圆能互相重合,所以是等弧,故③正确;在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
①③⑤
例2 矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
A
B
C
D
O
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
2.以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
3.下列说法中, 错误的有( )
(1)经过点P 的圆有无数个; (2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
解析:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,圆心和半径都确定,这样的圆有且只有一个(唯一).
A
4.如图,菱形ABCD的对角线AC和BD相交于点O.E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
分析:只需说明E,F,G,H 四点到点O 的距离相等即可.
解:点E,F,G,H 在同一个圆上,理由如下:
如图,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,∴ AB=BC=CD=DA,AC ⊥ BD.
又 E 为AB 边的中点,∴
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
圆
定义
有关概念
旋转定义:要画一个确定的圆,
关键是确定圆心和半径.
集合定义:同圆半径相等.
弦:直径是圆中最长的弦.
弧:劣弧、半圆、优弧.
24.1.1 圆
1.认识圆,理解圆的本质属性.
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.
圆是常见的几何图形,圆形物体在生活中随处可见.圆也是一种美丽的图形,具有独特的对称性,无论从哪个角度看,它都具有同一形状.十五的满月、圆圆的月饼象征着圆满、团圆、和谐.
本节我们将在前面学习的基础上,进一步认识圆,学习与圆有关的性质.
我们在小学已经对圆有了初步认识,如图,观察画圆的过程,你能说出圆是如何画出来的吗?
·
r
O
A
如图,在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 所形成的图形叫做圆.其固定的端点 O 叫做圆心,线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置;
二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“圆上的点”指圆周上的点.
(1) 圆上各点到定点(圆心O)的距离都等于 .
(2) 到定点的距离等于定长的点都在 .
定长 r
同一个圆上
想一想,从画圆的过程可以看出什么呢?
结论:
圆心为O,半径为 r 的圆可以看成是所有到定点O的距离等于定长 r 的点的集合.
C
A
·
O
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
圆中最长的弦是什么?为什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
根据三角形的三边关系判断.
圆中最长的弦
是直径.
·
C
O
A
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧:圆上任意两点间的部分叫做圆弧,简称弧.以A,B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧:小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
B
·
C
O
A
等圆: 能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出:等圆是两个半径相等的圆.
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
·
C
O
A
如图,如果弧AB和弧CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
这两条弧不可能完全重合,因为这两条弧弯曲程度不同,“等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或者等圆中.
特别提醒
1.弦与直径的关系:直径是过圆心最长的弦,但弦不一定是直径.
2.弧与半圆的关系:半圆是弧,但弧不一定是半圆.
3. 弦与弧的关系:
(1)弦是圆上两点间的线段,有无数条;弧是圆上两点间的部分,是曲线,也有无数条.
(2)每条弧对一条弦;而每条弦对的弧有两条:一条优弧、一条劣弧或两个半圆.
例1 下列语句中:①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,弧不一定是半圆. 正确的有_________ .
解析:直径是最长的弦,故①正确;直径是过圆心的弦,但弦不一定是直径,故②错误;半径相等的两个半圆能互相重合,所以是等弧,故③正确;在同圆或等圆中,长度相等的两条弧才是等弧,故④错误;弧分为劣弧、优弧、半圆,故⑤正确.
①③⑤
例2 矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
A
B
C
D
O
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
2.以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
3.下列说法中, 错误的有( )
(1)经过点P 的圆有无数个; (2)以点P 为圆心的圆有无数个;
(3)半径为3 cm 且经过点P 的圆有无数个;
(4)以点P 为圆心,3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
解析:确定一个圆必须有两个条件,即圆心和半径,只满足一个条件或不满足任何一个条件的圆都有无数个,圆心和半径都确定,这样的圆有且只有一个(唯一).
A
4.如图,菱形ABCD的对角线AC和BD相交于点O.E,F,G,H 分别为边AB,BC,CD,DA 的中点,那么点E,F,G,H 是否在同一个圆上?请说明理由.
分析:只需说明E,F,G,H 四点到点O 的距离相等即可.
解:点E,F,G,H 在同一个圆上,理由如下:
如图,连接OE,OF,OG,OH.
∵四边形ABCD 是菱形,∴ AB=BC=CD=DA,AC ⊥ BD.
又 E 为AB 边的中点,∴
同理可得,OF= BC,OG= CD,OH= DA.
∴ OE=OF=OG=OH.
∴点E,F,G,H 在以点O 为圆心,OE 为半径的圆上.
圆
定义
有关概念
旋转定义:要画一个确定的圆,
关键是确定圆心和半径.
集合定义:同圆半径相等.
弦:直径是圆中最长的弦.
弧:劣弧、半圆、优弧.
同课章节目录
