25.1.1 随机事件 课件(共23张PPT)
文档属性
| 名称 | 25.1.1 随机事件 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 699.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
25.1.1 随机事件
1. 会对必然事件,不可能事件和随机事件作出准确判断.
2. 归纳出必然事件、不可能事件和随机事件的特点.
3. 知道事件发生的可能性是有大小的.
我国有许多关于天气的谚语,例如:朝霞不出门,晚霞行千里,意思是早晨出现红霞,预示有雨,不宜出门;傍晚出现红霞,预示天晴,可以远行.
八月十五云遮月,正月十五雪打灯,意思是农历八月十五中秋节这天,如果天空被云幕遮蔽,看不到中秋圆月,来年正月十五这天就会下雪.
思考:以上谚语中的事件一定会发生吗?
问题一:五名同学参加演讲比赛,以抽签方式决定每个人的出场顺序. 为了抽签,在盒中放五个看上去完全一样的纸团里面分别写着表示出场顺序的数字 1,2,3,4,5. 把纸团充分搅拌后,小军先抽,他任意 ( 随机 ) 从盒中抽取一个纸团. 请思考以下问题:
解:数字 1,2,3,4,5 都有可能抽到,共有五种可能的结果,但是事先无法预料一次抽取会出现哪一种结果.
(1) 抽到的数字有几种可能的结果?
(2) 抽到的数字小于 6 吗?
(3) 抽到的数字会是 0 吗?
(4) 抽到的数字会是 1 吗?
抽到的数字一定小于 6;
抽到的数字绝对不会是 0;
抽到的数字可能是 1,也可能不是 1,事先无法确定.
问题二:小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有 1 到 6的点数. 请思考以下问题:掷一次骰子,在骰子向上的一面上,
从 1 到 6 的每一个点数都有可能出现,所有可能的点数共有 6 种,但是事先无法预料掷一次骰子会出现哪一种结果;
出现的点数肯定大于 0;
(1) 可能出现哪些点数?
(2) 出现的点数大于 0 吗?
(3) 出现的点数会是 7 吗?
(4) 出现的点数会是 4 吗?
在一定条件下,有些事件必然会发生,这样的事件称为必然事件.
相反地,有些事件必然不会发生,这样的事件称为不可能事件.
必然事件与不可能事件统称确定性事件.
在一定条件下,可能发生,也有可能不发生的事件,称为随机事件.
出现的点数绝对不会是 7;
出现的点数可能是 4,也可能不是 4,事先无法确定.
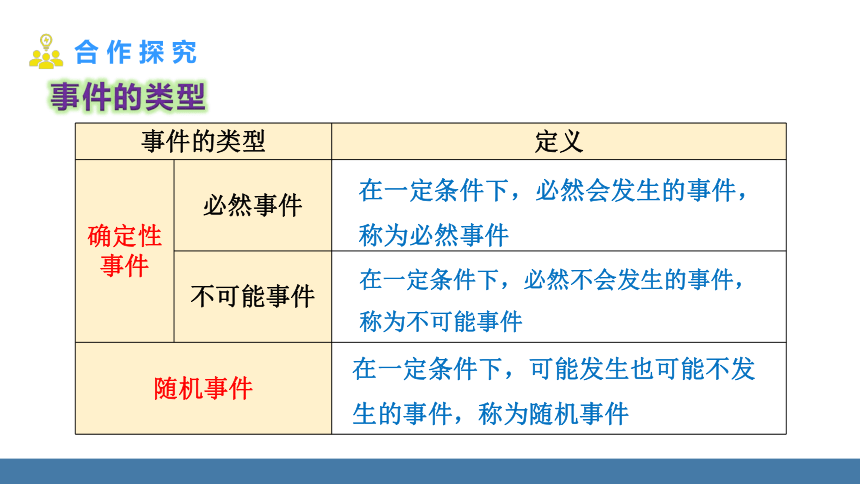
事件的类型
事件的类型 定义
确定性事件 必然事件
不可能事件
随机事件
在一定条件下,必然会发生的事件,称为必然事件
在一定条件下,必然不会发生的事件,
称为不可能事件
在一定条件下,可能发生也可能不发生的事件,称为随机事件
例1 指出下列事件中,哪些是必然事件,哪些是随机事件,
哪些是不可能事件.
(1)掷一枚质地均匀的硬币,正面朝上;
(2)买一张彩票,中一百万元;
(3)x2+1>0;
(4)任意买一张电影票,座位号是双号;
(5)向空中抛一枚质地均匀的硬币,硬币不向地面掉落.
必然事件
不可能事件
随机事件
随机事件
随机事件
判断一个事件的类型,要从其定义出发,同时也要联系理论及生活的相关常识来判断;注意必然事件和不可能事件都是事先可以确定的,一定发生的是必然事件,一定不发生的是不可能事件,否则就是随机事件.
问题三:袋子中装有 4 个黑球、2 个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别. 在看不到球的条件下,随机从袋子中摸出 1 个球.
(1) 这个球是白球还是黑球?
(2) 如果两种球都有可能被摸出,那么摸出黑球和白球的可能性一样大吗?
为了验证猜想,进行摸小球的实验. 请每名同学从袋里摸出 1 个球,记下球的颜色,然后把球放回袋子并摇匀,汇总摸球的结果并把结果填写在下表中.
球的颜色 黑球 白球
摸取次数
探 究
摸球结果和你事先的判断一致吗?
在前面的摸球活动中,“摸出黑球” 和“摸出白球” 是两个随机事件. 一次摸球可能发生“摸出黑球” ,也可能发生“摸出白球”,事先不能确定哪个事件发生. 由于两种球的数量不等,所以“摸出黑球”与“摸出白球”的可能性大小不一样. “摸出黑球”的可能性大于“摸出白球”的可能性.
归 纳
思 考
能否通过改变袋子中某种颜色的球的数量,使 “摸出黑球”和“摸出白球”的可能性大小相同?
可以增加 2 个白球,也可以减少 2 个黑球,使袋子中的两种球个数相同即可.
1. 随机事件发生的可能性是有大小的;
2. 不同的随机事件发生的可能性的大小有可能相同.
随机事件的特点
例2 如图,有一个转盘被分成 6 个相同的扇形,涂上红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个界线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色. 估计各事件的可能性大小,完成下题:
(1) 可能性最大的事件是_____,可能性最小的事件是 _____(填序号);
(2) 将这些事件的序号按发生的可能性从小到大的顺序排列是:_________.
④
②③①④
②
先要准确地找出所有可能出现的结果数,然后分情况,看每种情况包含的结果数与所有可能出现的结果数的比例大小.
比例越大,则这种情况发生的可能性越大.
判断随机事件发生的可能性大小的方法
事件发生的可能性
(1)必然事件:试验中必然发生的事件,其发生的可能性为100% 或1;
(2)不可能事件:试验中不可能发生的事件,其发生的可能性为0;
(3)随机事件:试验中可能发生也可能不发生的事件,其发生的可能性介于0 和1 之间.
1.指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)通常加热到 100℃ 时,水沸腾;
(2)篮球队员在罚球线上投篮一次,未投中;
(3)掷一次骰子,向上一面的点数是 6;
(4)任意画一个三角形,其内角和是 360°;
(5)经过有交通信号灯的路口,遇到红灯;
(6)射击运动员射击一次,命中靶心.
必然事件
随机事件
随机事件
不可能事件
随机事件
随机事件
2.在某校的乒乓球比赛中,李想同学顺利进入总决赛,且个人技艺高超,有同学预测“李想同学夺冠的可能性是80%”,对该同学的说法理解正确的是( )
A. 李想同学在比赛中有80% 的时间赢了对手
B. 李想同学和对手的10 局比赛中,一定赢8 局
C. 李想同学一定夺冠
D. 李想同学夺冠的可能性极大
D
3. 桌上倒扣着背面图案相同的 5 张扑克牌,其中 3 张黑桃、2 张红桃. 从中随机抽取一张.
(1) 能够事先确定抽取的扑克牌的花色吗?
(2) 你认为抽到哪种花色的可能性大?
不能确定
黑桃
(3) 能否通过改变某种花色的扑克牌的数量,使“抽到黑桃”和“抽到红桃”的可能性大小相同?
可以,去掉一张黑桃或增加一张红桃.
事 件
必然事件
随机事件
不可能事件
事件可能性大小
25.1.1 随机事件
1. 会对必然事件,不可能事件和随机事件作出准确判断.
2. 归纳出必然事件、不可能事件和随机事件的特点.
3. 知道事件发生的可能性是有大小的.
我国有许多关于天气的谚语,例如:朝霞不出门,晚霞行千里,意思是早晨出现红霞,预示有雨,不宜出门;傍晚出现红霞,预示天晴,可以远行.
八月十五云遮月,正月十五雪打灯,意思是农历八月十五中秋节这天,如果天空被云幕遮蔽,看不到中秋圆月,来年正月十五这天就会下雪.
思考:以上谚语中的事件一定会发生吗?
问题一:五名同学参加演讲比赛,以抽签方式决定每个人的出场顺序. 为了抽签,在盒中放五个看上去完全一样的纸团里面分别写着表示出场顺序的数字 1,2,3,4,5. 把纸团充分搅拌后,小军先抽,他任意 ( 随机 ) 从盒中抽取一个纸团. 请思考以下问题:
解:数字 1,2,3,4,5 都有可能抽到,共有五种可能的结果,但是事先无法预料一次抽取会出现哪一种结果.
(1) 抽到的数字有几种可能的结果?
(2) 抽到的数字小于 6 吗?
(3) 抽到的数字会是 0 吗?
(4) 抽到的数字会是 1 吗?
抽到的数字一定小于 6;
抽到的数字绝对不会是 0;
抽到的数字可能是 1,也可能不是 1,事先无法确定.
问题二:小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有 1 到 6的点数. 请思考以下问题:掷一次骰子,在骰子向上的一面上,
从 1 到 6 的每一个点数都有可能出现,所有可能的点数共有 6 种,但是事先无法预料掷一次骰子会出现哪一种结果;
出现的点数肯定大于 0;
(1) 可能出现哪些点数?
(2) 出现的点数大于 0 吗?
(3) 出现的点数会是 7 吗?
(4) 出现的点数会是 4 吗?
在一定条件下,有些事件必然会发生,这样的事件称为必然事件.
相反地,有些事件必然不会发生,这样的事件称为不可能事件.
必然事件与不可能事件统称确定性事件.
在一定条件下,可能发生,也有可能不发生的事件,称为随机事件.
出现的点数绝对不会是 7;
出现的点数可能是 4,也可能不是 4,事先无法确定.
事件的类型
事件的类型 定义
确定性事件 必然事件
不可能事件
随机事件
在一定条件下,必然会发生的事件,称为必然事件
在一定条件下,必然不会发生的事件,
称为不可能事件
在一定条件下,可能发生也可能不发生的事件,称为随机事件
例1 指出下列事件中,哪些是必然事件,哪些是随机事件,
哪些是不可能事件.
(1)掷一枚质地均匀的硬币,正面朝上;
(2)买一张彩票,中一百万元;
(3)x2+1>0;
(4)任意买一张电影票,座位号是双号;
(5)向空中抛一枚质地均匀的硬币,硬币不向地面掉落.
必然事件
不可能事件
随机事件
随机事件
随机事件
判断一个事件的类型,要从其定义出发,同时也要联系理论及生活的相关常识来判断;注意必然事件和不可能事件都是事先可以确定的,一定发生的是必然事件,一定不发生的是不可能事件,否则就是随机事件.
问题三:袋子中装有 4 个黑球、2 个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别. 在看不到球的条件下,随机从袋子中摸出 1 个球.
(1) 这个球是白球还是黑球?
(2) 如果两种球都有可能被摸出,那么摸出黑球和白球的可能性一样大吗?
为了验证猜想,进行摸小球的实验. 请每名同学从袋里摸出 1 个球,记下球的颜色,然后把球放回袋子并摇匀,汇总摸球的结果并把结果填写在下表中.
球的颜色 黑球 白球
摸取次数
探 究
摸球结果和你事先的判断一致吗?
在前面的摸球活动中,“摸出黑球” 和“摸出白球” 是两个随机事件. 一次摸球可能发生“摸出黑球” ,也可能发生“摸出白球”,事先不能确定哪个事件发生. 由于两种球的数量不等,所以“摸出黑球”与“摸出白球”的可能性大小不一样. “摸出黑球”的可能性大于“摸出白球”的可能性.
归 纳
思 考
能否通过改变袋子中某种颜色的球的数量,使 “摸出黑球”和“摸出白球”的可能性大小相同?
可以增加 2 个白球,也可以减少 2 个黑球,使袋子中的两种球个数相同即可.
1. 随机事件发生的可能性是有大小的;
2. 不同的随机事件发生的可能性的大小有可能相同.
随机事件的特点
例2 如图,有一个转盘被分成 6 个相同的扇形,涂上红、绿、黄三种颜色,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个界线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色. 估计各事件的可能性大小,完成下题:
(1) 可能性最大的事件是_____,可能性最小的事件是 _____(填序号);
(2) 将这些事件的序号按发生的可能性从小到大的顺序排列是:_________.
④
②③①④
②
先要准确地找出所有可能出现的结果数,然后分情况,看每种情况包含的结果数与所有可能出现的结果数的比例大小.
比例越大,则这种情况发生的可能性越大.
判断随机事件发生的可能性大小的方法
事件发生的可能性
(1)必然事件:试验中必然发生的事件,其发生的可能性为100% 或1;
(2)不可能事件:试验中不可能发生的事件,其发生的可能性为0;
(3)随机事件:试验中可能发生也可能不发生的事件,其发生的可能性介于0 和1 之间.
1.指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(1)通常加热到 100℃ 时,水沸腾;
(2)篮球队员在罚球线上投篮一次,未投中;
(3)掷一次骰子,向上一面的点数是 6;
(4)任意画一个三角形,其内角和是 360°;
(5)经过有交通信号灯的路口,遇到红灯;
(6)射击运动员射击一次,命中靶心.
必然事件
随机事件
随机事件
不可能事件
随机事件
随机事件
2.在某校的乒乓球比赛中,李想同学顺利进入总决赛,且个人技艺高超,有同学预测“李想同学夺冠的可能性是80%”,对该同学的说法理解正确的是( )
A. 李想同学在比赛中有80% 的时间赢了对手
B. 李想同学和对手的10 局比赛中,一定赢8 局
C. 李想同学一定夺冠
D. 李想同学夺冠的可能性极大
D
3. 桌上倒扣着背面图案相同的 5 张扑克牌,其中 3 张黑桃、2 张红桃. 从中随机抽取一张.
(1) 能够事先确定抽取的扑克牌的花色吗?
(2) 你认为抽到哪种花色的可能性大?
不能确定
黑桃
(3) 能否通过改变某种花色的扑克牌的数量,使“抽到黑桃”和“抽到红桃”的可能性大小相同?
可以,去掉一张黑桃或增加一张红桃.
事 件
必然事件
随机事件
不可能事件
事件可能性大小
同课章节目录
