25.2.1 用直接列举法求概率 课件(共24张PPT)
文档属性
| 名称 | 25.2.1 用直接列举法求概率 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 718.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 22:07:51 | ||
图片预览








文档简介
(共24张PPT)
25.2.1 用直接列举法求概率
1. 知道什么时候采用“直接列举法”和“列表法”.
2. 会正确“列表”表示出所有可能出现的结果.
3. 知道如何利用“列表法”求随机事件的概率.
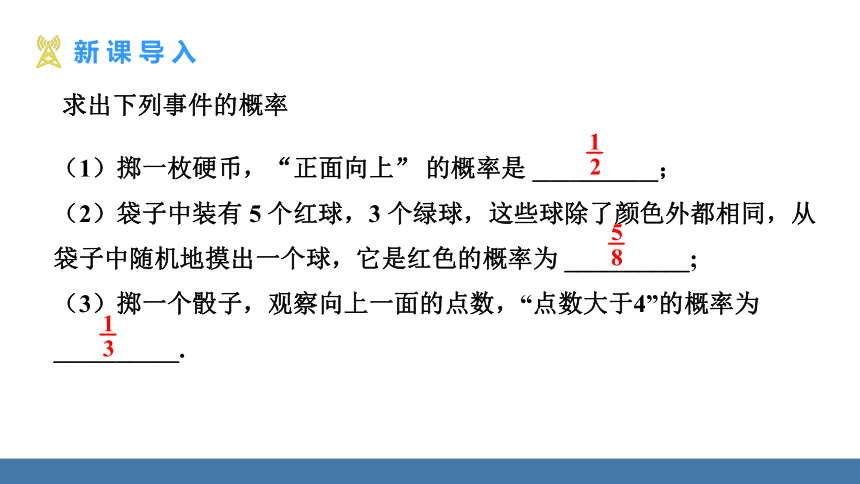
求出下列事件的概率
(1)掷一枚硬币,“正面向上” 的概率是 __________;
(2)袋子中装有 5 个红球,3 个绿球,这些球除了颜色外都相同,从袋子中随机地摸出一个球,它是红色的概率为 __________;
(3)掷一个骰子,观察向上一面的点数,“点数大于4”的概率为__________.
在以上试验中,可能出现的结果只有有限种,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫做列举法.
例1 同时向空中抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:
正正,正反,反正,反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有1种,即“正正”,所以
P(A)= .
(2) 两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,所以
P(B)= .
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,所以
P(C)= .
对于抛掷两枚硬币的问题,如何才能不重不漏地列举出试验的所有结果,并且保证各种结果出现的可能性大小相等?
将两枚硬币分别记做 A,B,于是可以直接列举得到(A正, B正)、(A反, B正)、(A正, B反)、(A反, B反)四种等可能的结果.
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
思 考
“同时抛掷两枚质地均匀的硬币”与“先后抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
分步思考:(1)在第一枚为正面的情况下第二枚硬币有正、反两种情况; (2)第一枚为反面的情况下第二枚硬币有正、反两种情况. 所有的结果共有 4 个,并且这 4 个结果的可能性相等.
“同时掷两枚硬币”与“先后两次掷一枚硬币”可以取同样的试验的所有可能结果. 因此可以将同时掷两枚硬币,想象为先掷一枚,再掷一枚.
能否设计出一种方式,将“分步”分析的所有结果更清晰的列举出来?
第一枚 第二枚 正 反
正 正正 反正
反 正反 反反
在设计表格时,表头的横行、竖列分别表示什么?每个格表示什么?
表头的横行表示掷第一枚硬币所有可能的结果,竖列表示掷第二枚硬币所有可能的结果.
表格中的每个格表示掷两枚硬币的一种可能结果.
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子的点数和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
第一枚 第二枚 1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
试验涉及几个因素?能否直接列出试验所有可能的结果.
通过列表法可知,同时掷两枚骰子,共有 36 种可能的结果,并且它们发生的可能性相等.
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的蓝色铺底部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的黄色铺底部分),即(3,6),(4,5),(5,4),(6,3),所以
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中红色方框部分),所以
用列表法求概率适用于事件中涉及两个因素,并且可能出现的结果数目较多的概率问题.
在运用列表法求概率时,应注意各种结果出现的可能性相等,要注意列表的顺序,并不重不漏地列出所有可能的结果.
列表法具体步骤
(1)选其中的一次操作(或一个条件)为横行,另一次操作(或另一个条件)为纵列,列出表格;
(2)运用概率公式P(A)= 计算概率.
特别提醒
1. 列表法适用于求两步试验的概率,利用表格的行和列,分别表示出试验涉及的两次操作或两个条件.
2. 列表法不适用于求三步及三步以上试验的概率.
3. 在运用列表法分析随机事件发生的概率时,数据或事件的顺序不能混淆,如(1,2)与(2,1)不是相同的事件.
1.从-3,-1,0,2 四个数中任选两个,则这两个数的乘积为
负数的概率为( )
B
2. 假定鸟卵孵化后,雏鸟为雌与为雄的概率相同. 如果两枚卵全部成功孵化,则两只雏鸟都为雄鸟的概率为多少?
第一只 第二只 雄 雌
雄 雄,雄 雌,雄
雌 雄,雌 雌,雌
解:列表如下:
∴P(两只雏鸟都为雄鸟) = .
3.某景区7 月1 日~7 月7 日一周天气预报如图,小丽打算选择这期间的1 天或2 天去该景区旅游,求下列事件的概率:
(1)随机选择1 天,恰好天气预报是晴;
解:∵在这7 天中,天气预报是晴的有4 天,
∴ P(随机选择1 天,恰好天气预报是晴)=
3.某景区7 月1 日~7 月7 日一周天气预报如图,小丽打算选择这期间的1 天或2 天去该景区旅游,求下列事件的概率:
(2)随机选择连续的2 天,恰好天气预报都是晴.
解:∵随机选择连续的2 天,天气预报可能出现的结果有6 种:晴晴,晴雨,雨阴,阴晴,晴晴,晴阴,且每种结果出现的可能性相等,
∴ P(随机选择连续的2 天,恰好天气预报都是晴)=
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验
基本步骤
列表;
确定m,n值,
代入概率公式计算
正确列举出试验结果的各种可能性
确保试验中每种结果出现的可能性大小相等
前提条件
25.2.1 用直接列举法求概率
1. 知道什么时候采用“直接列举法”和“列表法”.
2. 会正确“列表”表示出所有可能出现的结果.
3. 知道如何利用“列表法”求随机事件的概率.
求出下列事件的概率
(1)掷一枚硬币,“正面向上” 的概率是 __________;
(2)袋子中装有 5 个红球,3 个绿球,这些球除了颜色外都相同,从袋子中随机地摸出一个球,它是红色的概率为 __________;
(3)掷一个骰子,观察向上一面的点数,“点数大于4”的概率为__________.
在以上试验中,可能出现的结果只有有限种,且各种结果出现的可能性大小相等,那么我们可以通过列举试验结果的方法,求出随机事件发生的概率,这种求概率的方法叫做列举法.
例1 同时向空中抛掷两枚质地均匀的硬币,求下列事件的概率:
(1)两枚硬币全部向上;
(2)两枚硬币全部反面向上;
(3)一枚硬币正面向上,一枚硬币反面向上.
解:列举抛掷两枚硬币所能产生的全部结果,它们是:
正正,正反,反正,反反.
所有可能的结果共有4种,并且这4种结果出现的可能性相等.
(1)所有可能的结果中,满足两枚硬币全部正面向上(记为事件A)的结果只有1种,即“正正”,所以
P(A)= .
(2) 两枚硬币全部反面向上(记为事件B)的结果也只有1种,即“反反”,所以
P(B)= .
(3)一枚硬币正面向上、一枚硬币反面向上(记为事件C)的结果共有2种,即“反正”“正反”,所以
P(C)= .
对于抛掷两枚硬币的问题,如何才能不重不漏地列举出试验的所有结果,并且保证各种结果出现的可能性大小相等?
将两枚硬币分别记做 A,B,于是可以直接列举得到(A正, B正)、(A反, B正)、(A正, B反)、(A反, B反)四种等可能的结果.
上述这种列举法我们称为直接列举法,即把事件可能出现的结果一一列出.
直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验,且事件总结果的种数比较少的等可能性事件.
思 考
“同时抛掷两枚质地均匀的硬币”与“先后抛掷一枚质地均匀的硬币”,这两种试验的所有可能结果一样吗?
分步思考:(1)在第一枚为正面的情况下第二枚硬币有正、反两种情况; (2)第一枚为反面的情况下第二枚硬币有正、反两种情况. 所有的结果共有 4 个,并且这 4 个结果的可能性相等.
“同时掷两枚硬币”与“先后两次掷一枚硬币”可以取同样的试验的所有可能结果. 因此可以将同时掷两枚硬币,想象为先掷一枚,再掷一枚.
能否设计出一种方式,将“分步”分析的所有结果更清晰的列举出来?
第一枚 第二枚 正 反
正 正正 反正
反 正反 反反
在设计表格时,表头的横行、竖列分别表示什么?每个格表示什么?
表头的横行表示掷第一枚硬币所有可能的结果,竖列表示掷第二枚硬币所有可能的结果.
表格中的每个格表示掷两枚硬币的一种可能结果.
例2 同时掷两枚质地均匀的骰子,计算下列事件的概率:
(1)两枚骰子的点数相同;
(2)两枚骰子的点数和是9;
(3)至少有一枚骰子的点数为2.
分析:当一次试验是掷两枚骰子时,为不重不漏地列出所有可能的结果,通常采用列表法.
第一枚 第二枚 1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,6) (6,6)
试验涉及几个因素?能否直接列出试验所有可能的结果.
通过列表法可知,同时掷两枚骰子,共有 36 种可能的结果,并且它们发生的可能性相等.
(1)两枚骰子的点数相同(记为事件A)的结果有6种(表中的蓝色铺底部分),即(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),所以
(2)两枚骰子的点数和是9(记为事件B)的结果有4种(表中的黄色铺底部分),即(3,6),(4,5),(5,4),(6,3),所以
(3)至少有一枚骰子的点数为2(记为事件C)的结果有11种(表中红色方框部分),所以
用列表法求概率适用于事件中涉及两个因素,并且可能出现的结果数目较多的概率问题.
在运用列表法求概率时,应注意各种结果出现的可能性相等,要注意列表的顺序,并不重不漏地列出所有可能的结果.
列表法具体步骤
(1)选其中的一次操作(或一个条件)为横行,另一次操作(或另一个条件)为纵列,列出表格;
(2)运用概率公式P(A)= 计算概率.
特别提醒
1. 列表法适用于求两步试验的概率,利用表格的行和列,分别表示出试验涉及的两次操作或两个条件.
2. 列表法不适用于求三步及三步以上试验的概率.
3. 在运用列表法分析随机事件发生的概率时,数据或事件的顺序不能混淆,如(1,2)与(2,1)不是相同的事件.
1.从-3,-1,0,2 四个数中任选两个,则这两个数的乘积为
负数的概率为( )
B
2. 假定鸟卵孵化后,雏鸟为雌与为雄的概率相同. 如果两枚卵全部成功孵化,则两只雏鸟都为雄鸟的概率为多少?
第一只 第二只 雄 雌
雄 雄,雄 雌,雄
雌 雄,雌 雌,雌
解:列表如下:
∴P(两只雏鸟都为雄鸟) = .
3.某景区7 月1 日~7 月7 日一周天气预报如图,小丽打算选择这期间的1 天或2 天去该景区旅游,求下列事件的概率:
(1)随机选择1 天,恰好天气预报是晴;
解:∵在这7 天中,天气预报是晴的有4 天,
∴ P(随机选择1 天,恰好天气预报是晴)=
3.某景区7 月1 日~7 月7 日一周天气预报如图,小丽打算选择这期间的1 天或2 天去该景区旅游,求下列事件的概率:
(2)随机选择连续的2 天,恰好天气预报都是晴.
解:∵随机选择连续的2 天,天气预报可能出现的结果有6 种:晴晴,晴雨,雨阴,阴晴,晴晴,晴阴,且每种结果出现的可能性相等,
∴ P(随机选择连续的2 天,恰好天气预报都是晴)=
列举法
关键
常用
方法
直接列举法
列表法
适用对象
两个试验因素或分两步进行的试验
基本步骤
列表;
确定m,n值,
代入概率公式计算
正确列举出试验结果的各种可能性
确保试验中每种结果出现的可能性大小相等
前提条件
同课章节目录
