25.2.2 用画树状图法求概率 课件(共22张PPT)
文档属性
| 名称 | 25.2.2 用画树状图法求概率 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 908.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 22:07:01 | ||
图片预览






文档简介
(共22张PPT)
25.2.2 用画树状图法求概率
1. 进一步理解等可能事件概率的意义.
2. 学习运用树状图计算事件的概率.
3. 会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.
小明参与刮刮乐的游戏,需要刮3张票,每张票都有A,B两种结果,当3张票上的字母都相同时,就可以赢得一等奖,获奖的几率是多少?
是否可以用列表法列举出所有的情况呢?
一共要刮 3 次,列表法只能表示两个因素之间的关系,所以不能用列表法来列举.
探 究
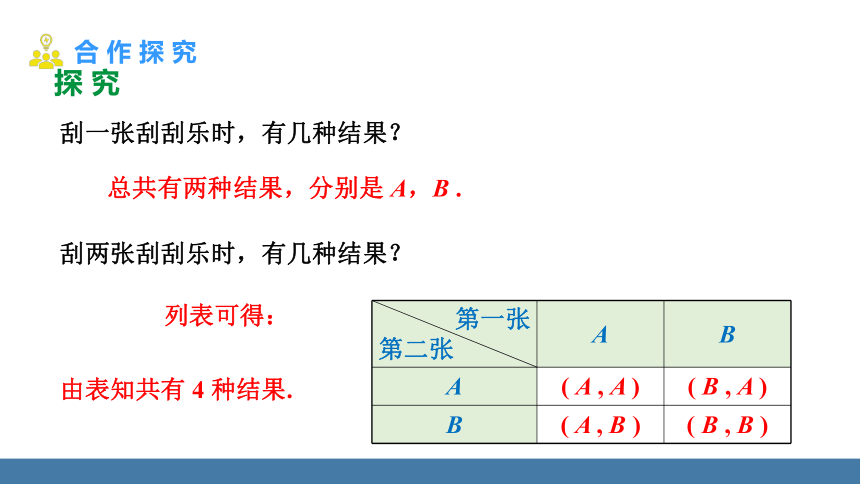
刮一张刮刮乐时,有几种结果?
刮两张刮刮乐时,有几种结果?
第一张 第二张 A B
A ( A , A ) ( B , A )
B ( A , B ) ( B , B )
由表知共有 4 种结果.
总共有两种结果,分别是 A,B .
列表可得:
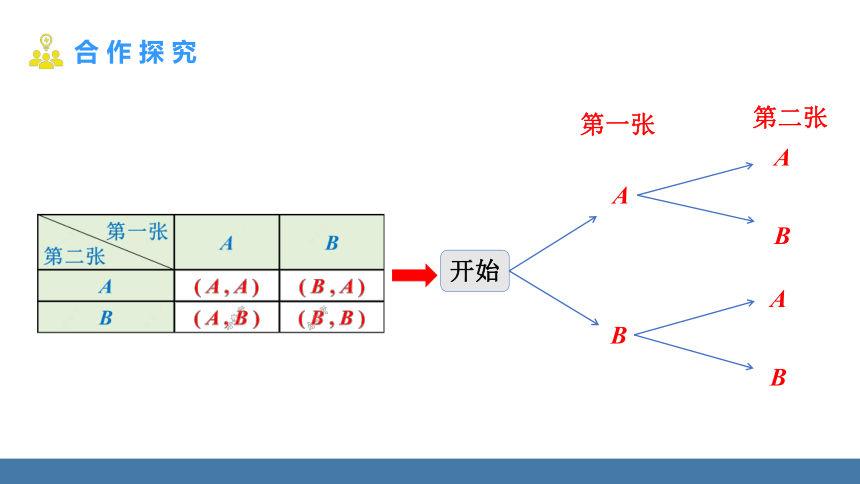
开始
第一张
第二张
A
B
A
B
A
B
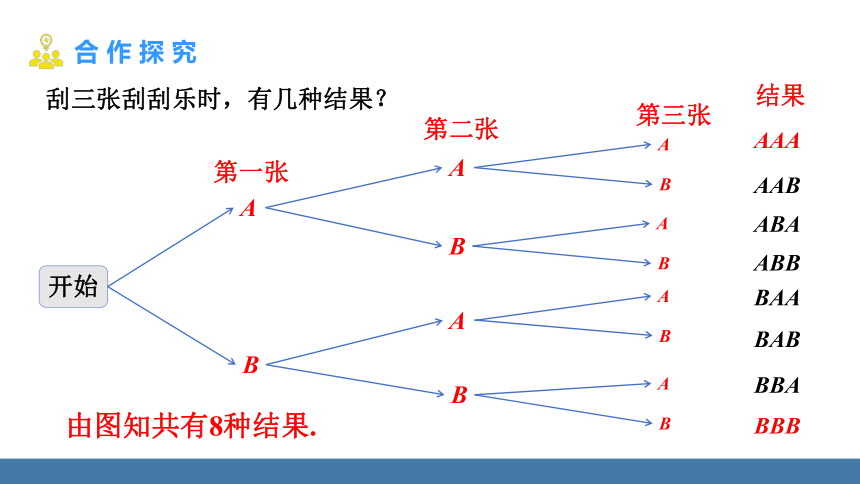
刮三张刮刮乐时,有几种结果?
开始
第一张
第二张
A
B
A
A
B
B
第三张
A
B
A
B
A
B
A
B
AAA
AAB
ABA
ABB
BAA
BAB
BBA
BBB
结果
由图知共有8种结果.
在刮三张刮刮乐的试验中,需要分三步完成,每一步确定 1 个字母,因此每种结果中包含 3 个字母. 如果用列表法,则需要用到三维表格,这在二维平面上难以表现,因此不宜用列表法. 画树状图是一种解决试验由多步 ( 或涉及多个因素 ) 完成问题的好方法.
画树状图法是用树状图的形式反映各种事件发生所有可能出现的结果和次数,以及某一事件发生出现的结果和次数,并求出概率的方法.
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤和顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件 A 包含的结果数 m,试验的所有可能结果数 n;
(4)用概率公式进行计算.
例 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装 有3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,它们分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球.
(1) 取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2) 取出的3个小球上全部是辅音字母的概率是多少?
本题中,A,E,I是元音字母;
B,C,D,H是辅音字母.
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用画树状图法.
解:根据题意,可以画出如下树状图:
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
由树状图可以看出,所有可能出现的结果共有12种,即
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
这些结果出现的可能性相等.
(1) 只有 1 个元音字母的结果 有 5 种,即 ACH,ADH,BCI,BDI,BEH,所以 P(1个元音) = .
有2个元音字母的结果 有 4 种,即 ACI,ADI,AEH,BEI,
所以 P(2个元音) = = .
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
(1)全部为元音字母的结果 有 1 种,即 AEI,
所以 P(3个元音) = .
(2) 全部是辅音字母的结果 有 2 种,即 BCH,BDH,
所以 P(3个辅音) = = .
用树状图列举的结果看起来一目了然,当事件要经过多个步骤 ( 三步或三步以上 ) 完成时,用画树状图法求事件的概率很有效.
特别提醒
1. 用列表法或画树状图法求事件的概率时,应注意各种情况出现的可能性必须相等.
2. 当试验包含两步时,用列表法比较方便,当然此时也可用画树状图法. 当试验在三步或三步以上时,用画树状图法比较方便,此时,不宜用列表法.
1.A,B,C 三人玩篮球传球游戏,游戏规则是:第一次传球由A 将球随机地传给B,C 两人中的某一人,以后的每一次传球都是由上次的接球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰好在B 手中的概率;
解:画树状图如图.由树状图知,共有4 种等可能的结果,两次传球后,球恰好在B 手中的结果只有1 种,所以两次传球后,球恰好在B 手中的概率为
1.A,B,C 三人玩篮球传球游戏,游戏规则是:第一次传球由A 将球随机地传给B,C 两人中的某一人,以后的每一次传球都是由上次的接球者随机地传给其他两人中的某一人.
(2)求三次传球后,球恰好在A 手中的概率.
解:画树状图如图. 由树状图知,共有8 种等可能的结果,三次传球后,球恰好在A 手中的结果有2 种,所以三次传球后,球恰好在A 手中的概率为
2.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1) 三辆车全部继续直行;
(2) 两辆车向右转,一辆车向左转;
(3) 至少两辆车向左转.
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
解:根据题意,可以画出如下树状图:
共有27种等可能行驶结果.
(2) P(两车向右,一车向左) = ;
(1) P(全部继续直行) = ;
(3) P(至少两车向左) =
树状图
步骤
用法
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果,并找出事件所包含的结果数;
利用概率公式进行计算.
是一种解决试验有多步(或涉及多个因素)的好方法.
25.2.2 用画树状图法求概率
1. 进一步理解等可能事件概率的意义.
2. 学习运用树状图计算事件的概率.
3. 会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.
小明参与刮刮乐的游戏,需要刮3张票,每张票都有A,B两种结果,当3张票上的字母都相同时,就可以赢得一等奖,获奖的几率是多少?
是否可以用列表法列举出所有的情况呢?
一共要刮 3 次,列表法只能表示两个因素之间的关系,所以不能用列表法来列举.
探 究
刮一张刮刮乐时,有几种结果?
刮两张刮刮乐时,有几种结果?
第一张 第二张 A B
A ( A , A ) ( B , A )
B ( A , B ) ( B , B )
由表知共有 4 种结果.
总共有两种结果,分别是 A,B .
列表可得:
开始
第一张
第二张
A
B
A
B
A
B
刮三张刮刮乐时,有几种结果?
开始
第一张
第二张
A
B
A
A
B
B
第三张
A
B
A
B
A
B
A
B
AAA
AAB
ABA
ABB
BAA
BAB
BBA
BBB
结果
由图知共有8种结果.
在刮三张刮刮乐的试验中,需要分三步完成,每一步确定 1 个字母,因此每种结果中包含 3 个字母. 如果用列表法,则需要用到三维表格,这在二维平面上难以表现,因此不宜用列表法. 画树状图是一种解决试验由多步 ( 或涉及多个因素 ) 完成问题的好方法.
画树状图法是用树状图的形式反映各种事件发生所有可能出现的结果和次数,以及某一事件发生出现的结果和次数,并求出概率的方法.
画树状图求概率的基本步骤
(1)明确一次试验的几个步骤和顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出随机事件 A 包含的结果数 m,试验的所有可能结果数 n;
(4)用概率公式进行计算.
例 甲口袋中装有 2 个相同的小球,它们分别写有字母 A 和 B;乙口袋中装 有3 个相同的小球,它们分别写有字母 C,D 和 E;丙口袋中装有 2 个相同的小球,它们分别写有字母 H 和 I. 从三个口袋中各随机取出 1 个小球.
(1) 取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2) 取出的3个小球上全部是辅音字母的概率是多少?
本题中,A,E,I是元音字母;
B,C,D,H是辅音字母.
分析:当一次试验是从三个口袋中取球时,列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用画树状图法.
解:根据题意,可以画出如下树状图:
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
由树状图可以看出,所有可能出现的结果共有12种,即
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
这些结果出现的可能性相等.
(1) 只有 1 个元音字母的结果 有 5 种,即 ACH,ADH,BCI,BDI,BEH,所以 P(1个元音) = .
有2个元音字母的结果 有 4 种,即 ACI,ADI,AEH,BEI,
所以 P(2个元音) = = .
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
ACH
ACI
ADH
ADI
AEH
AEI
BCH
BCI
BDH
BDI
BEH
BEI
(1)全部为元音字母的结果 有 1 种,即 AEI,
所以 P(3个元音) = .
(2) 全部是辅音字母的结果 有 2 种,即 BCH,BDH,
所以 P(3个辅音) = = .
用树状图列举的结果看起来一目了然,当事件要经过多个步骤 ( 三步或三步以上 ) 完成时,用画树状图法求事件的概率很有效.
特别提醒
1. 用列表法或画树状图法求事件的概率时,应注意各种情况出现的可能性必须相等.
2. 当试验包含两步时,用列表法比较方便,当然此时也可用画树状图法. 当试验在三步或三步以上时,用画树状图法比较方便,此时,不宜用列表法.
1.A,B,C 三人玩篮球传球游戏,游戏规则是:第一次传球由A 将球随机地传给B,C 两人中的某一人,以后的每一次传球都是由上次的接球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰好在B 手中的概率;
解:画树状图如图.由树状图知,共有4 种等可能的结果,两次传球后,球恰好在B 手中的结果只有1 种,所以两次传球后,球恰好在B 手中的概率为
1.A,B,C 三人玩篮球传球游戏,游戏规则是:第一次传球由A 将球随机地传给B,C 两人中的某一人,以后的每一次传球都是由上次的接球者随机地传给其他两人中的某一人.
(2)求三次传球后,球恰好在A 手中的概率.
解:画树状图如图. 由树状图知,共有8 种等可能的结果,三次传球后,球恰好在A 手中的结果有2 种,所以三次传球后,球恰好在A 手中的概率为
2.经过某十字路口的汽车,可能直行,也可能向左转或向右转,如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1) 三辆车全部继续直行;
(2) 两辆车向右转,一辆车向左转;
(3) 至少两辆车向左转.
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
解:根据题意,可以画出如下树状图:
共有27种等可能行驶结果.
(2) P(两车向右,一车向左) = ;
(1) P(全部继续直行) = ;
(3) P(至少两车向左) =
树状图
步骤
用法
注意
弄清试验涉及试验因素个数或试验步骤分几步;
在摸球试验一定要弄清“放回”还是“不放回”.
关键要弄清楚每一步有几种结果;
在树状图下面对应写着所有可能的结果,并找出事件所包含的结果数;
利用概率公式进行计算.
是一种解决试验有多步(或涉及多个因素)的好方法.
同课章节目录
