24.4.2 圆锥的侧面积和全面积 课件(共21张PPT)
文档属性
| 名称 | 24.4.2 圆锥的侧面积和全面积 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 22:05:32 | ||
图片预览





文档简介
(共21张PPT)
24.4.2 圆锥的侧面积和全面积
1.体会圆锥侧面积的探索过程.
2.会求圆锥的侧面积,并能解决一些简单的实际问题.
圆锥是由一个底面和一个侧面围成的几何体,圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周所形成的图形,这条直线叫做圆锥的轴.
圆锥的概念
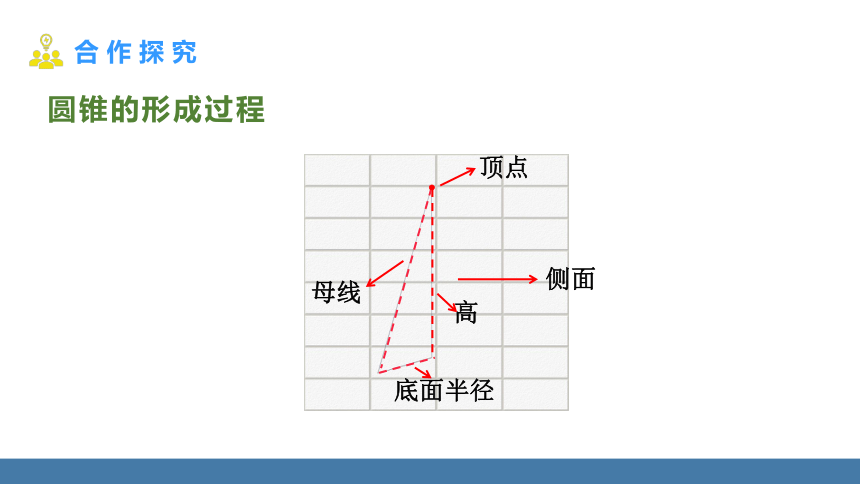
顶点
母线
底面半径
侧面
高
圆锥的形成过程
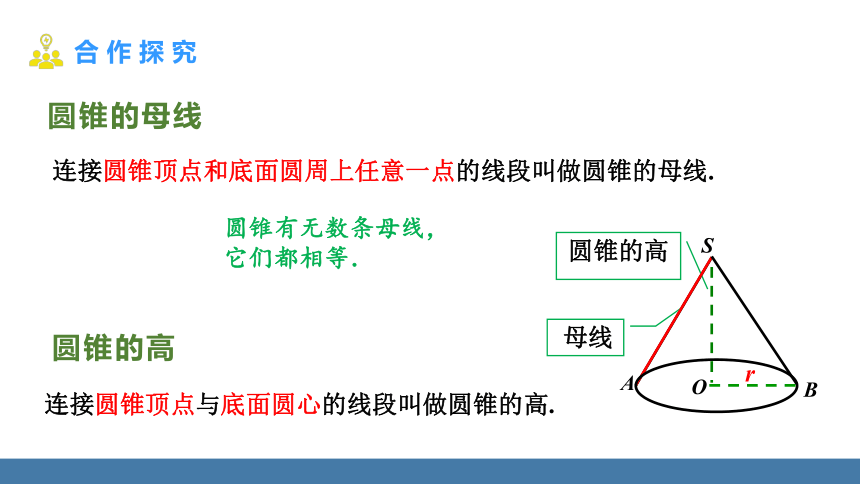
连接圆锥顶点与底面圆心的线段叫做圆锥的高.
圆锥的母线
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
圆锥的高
母线
S
A
O
B
r
圆锥的高
圆锥有无数条母线,
它们都相等.
如果用 r 表示圆锥底面圆的半径,h 表示圆锥的高线长,l 表示圆锥的母线长,那么r,h,l 之间的数量关系是:__________.
h
O
r
r2+h2=l2
归 纳
思 考
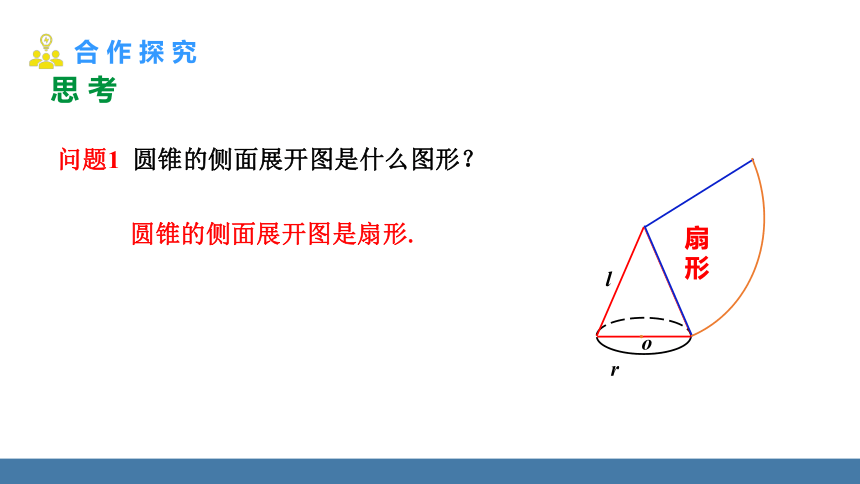
问题1 圆锥的侧面展开图是什么图形?
l
o
r
扇形
圆锥的侧面展开图是扇形.
问题2 沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题3 圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
相等
母线
l
O
侧面
展开图
l
r
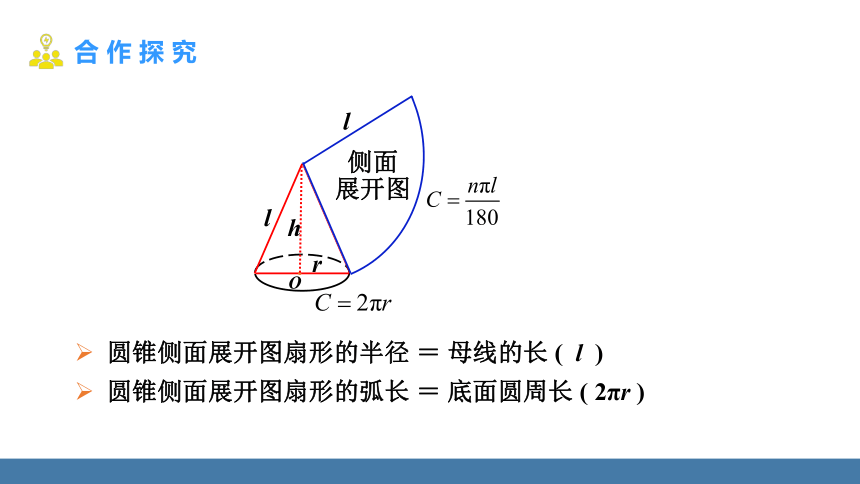
圆锥侧面展开图扇形的半径 = 母线的长 ( l )
圆锥侧面展开图扇形的弧长 = 底面圆周长 ( 2πr )
h
我们已经知道圆锥的侧面展开图是一个扇形,并且上节课已经学习了扇形的面积公式,那么我们能不能据此推导出圆锥的侧面积和全面积公式呢?下面我们一起来看一下.
圆锥的侧面积计算公式
l
O
侧面
展开图
底面圆
l
r
圆锥的全面积计算公式
∴S侧 = πrl ( r 表示圆锥底面圆的半径,
l 表示圆锥的母线长 ).
例1 如图,在△ ABC 中,∠ C= 90°,AC=6,BC=8.
(1)将△ ABC 以BC 所在直线为轴旋转一周,求所得旋转体的全面积;
(2)将△ ABC 以AC 所在直线为轴旋转一周,求所得旋转体的全面积.
分析:所得旋转体是一个圆锥,其全面积等于侧面展开图的扇形的面积与底面圆的面积之和.
解:(1)∵∠ C=90°,AC=6,BC=8,
∴ AB= =10.
∴ S底=π×AC2=36π,S侧=π×6×10=60π.
∴ S全=S底+S侧=96π.
(2)S底=π×BC2=64π,S侧=π×8×10=80π,
∴ S全=S底+S侧=144π.
例2 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建 20个底面积为 12 m2,高为 3.2 m,外围高 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π取3.142,结果取整数 )
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为 12 m2,高 h2=1.8 m;
上部圆锥的高 h1=3.2-1.8=1.4(m).
h1
h2
r
圆柱的底面圆的半径 r =
侧面积为 2π×1.954×1.8≈22.10 (m2).
侧面展开扇形的弧长为 2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建 20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
圆锥的母线长 l =
h1
h2
r
1.若一个圆锥的侧面展开图是半径为 18 cm,圆心角为 240° 的扇形,则这个圆锥的底面半径是( )
A. 6 cm
B. 9 cm
C. 12 cm
D. 18 cm
C
2. 圆锥的底面半径为 3 cm,母线长为 6 cm,则这个圆
锥侧面展开图扇形的圆心角是_____.
3. 一个扇形,半径为 30 cm,圆心角为 120°,用它做成
一个圆锥的侧面,那么这个圆锥的底面半径为 .
4. 已知圆锥的底面圆半径为 3 cm,高为 4 cm,则它的
侧面积是 ,全面积是 .
180°
10 cm
15π cm2
24π cm2
5.如图,已知扇形OAB的半径为6 cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)围成的圆锥的侧面积为多少?
∴圆锥的侧面积 .
解:由已知得扇形的半径 R = 6cm.
(2) 该圆锥的底面半径是多少?
根据题意得 ,解得 r=2.
解:该圆锥的底面半径为r cm,
即圆锥的底面半径为 2 cm.
1. 连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
2. 圆锥的侧面展开图是扇形.
3. 圆锥的侧面积及全面积公式:
S侧=πrl,
S全=S侧+S底= πrl+ πr2=πr(r+l).
24.4.2 圆锥的侧面积和全面积
1.体会圆锥侧面积的探索过程.
2.会求圆锥的侧面积,并能解决一些简单的实际问题.
圆锥是由一个底面和一个侧面围成的几何体,圆锥可以看作是一个直角三角形绕它的一条直角边所在的直线旋转一周所形成的图形,这条直线叫做圆锥的轴.
圆锥的概念
顶点
母线
底面半径
侧面
高
圆锥的形成过程
连接圆锥顶点与底面圆心的线段叫做圆锥的高.
圆锥的母线
连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
圆锥的高
母线
S
A
O
B
r
圆锥的高
圆锥有无数条母线,
它们都相等.
如果用 r 表示圆锥底面圆的半径,h 表示圆锥的高线长,l 表示圆锥的母线长,那么r,h,l 之间的数量关系是:__________.
h
O
r
r2+h2=l2
归 纳
思 考
问题1 圆锥的侧面展开图是什么图形?
l
o
r
扇形
圆锥的侧面展开图是扇形.
问题2 沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题3 圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
相等
母线
l
O
侧面
展开图
l
r
圆锥侧面展开图扇形的半径 = 母线的长 ( l )
圆锥侧面展开图扇形的弧长 = 底面圆周长 ( 2πr )
h
我们已经知道圆锥的侧面展开图是一个扇形,并且上节课已经学习了扇形的面积公式,那么我们能不能据此推导出圆锥的侧面积和全面积公式呢?下面我们一起来看一下.
圆锥的侧面积计算公式
l
O
侧面
展开图
底面圆
l
r
圆锥的全面积计算公式
∴S侧 = πrl ( r 表示圆锥底面圆的半径,
l 表示圆锥的母线长 ).
例1 如图,在△ ABC 中,∠ C= 90°,AC=6,BC=8.
(1)将△ ABC 以BC 所在直线为轴旋转一周,求所得旋转体的全面积;
(2)将△ ABC 以AC 所在直线为轴旋转一周,求所得旋转体的全面积.
分析:所得旋转体是一个圆锥,其全面积等于侧面展开图的扇形的面积与底面圆的面积之和.
解:(1)∵∠ C=90°,AC=6,BC=8,
∴ AB= =10.
∴ S底=π×AC2=36π,S侧=π×6×10=60π.
∴ S全=S底+S侧=96π.
(2)S底=π×BC2=64π,S侧=π×8×10=80π,
∴ S全=S底+S侧=144π.
例2 蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建 20个底面积为 12 m2,高为 3.2 m,外围高 1.8 m 的蒙古包,至少需要多少平方米的毛毡 ( π取3.142,结果取整数 )
解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为 12 m2,高 h2=1.8 m;
上部圆锥的高 h1=3.2-1.8=1.4(m).
h1
h2
r
圆柱的底面圆的半径 r =
侧面积为 2π×1.954×1.8≈22.10 (m2).
侧面展开扇形的弧长为 2π×1.954≈12.28(m),
圆锥的侧面积为 ×2.404×12.28≈14.76(m2).
因此,搭建 20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
圆锥的母线长 l =
h1
h2
r
1.若一个圆锥的侧面展开图是半径为 18 cm,圆心角为 240° 的扇形,则这个圆锥的底面半径是( )
A. 6 cm
B. 9 cm
C. 12 cm
D. 18 cm
C
2. 圆锥的底面半径为 3 cm,母线长为 6 cm,则这个圆
锥侧面展开图扇形的圆心角是_____.
3. 一个扇形,半径为 30 cm,圆心角为 120°,用它做成
一个圆锥的侧面,那么这个圆锥的底面半径为 .
4. 已知圆锥的底面圆半径为 3 cm,高为 4 cm,则它的
侧面积是 ,全面积是 .
180°
10 cm
15π cm2
24π cm2
5.如图,已知扇形OAB的半径为6 cm,圆心角的度数为120°,若将此扇形围成一个圆锥,则:
(1)围成的圆锥的侧面积为多少?
∴圆锥的侧面积 .
解:由已知得扇形的半径 R = 6cm.
(2) 该圆锥的底面半径是多少?
根据题意得 ,解得 r=2.
解:该圆锥的底面半径为r cm,
即圆锥的底面半径为 2 cm.
1. 连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.
2. 圆锥的侧面展开图是扇形.
3. 圆锥的侧面积及全面积公式:
S侧=πrl,
S全=S侧+S底= πrl+ πr2=πr(r+l).
同课章节目录
