人教版八年级下册17.1勾股定理 课件(共23张PPT)
文档属性
| 名称 | 人教版八年级下册17.1勾股定理 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 10:19:59 | ||
图片预览





文档简介
(共23张PPT)
人教版八年级数学下册
第17章 勾股定理
17.1 勾股定理 第一课时
学习目标
1、经历勾股定理的探究过程,了解关于勾股定理的文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想。
2、培养在实际生活中发现问题总结规律的意识和能力。
学习重点
理解勾股定理的证明方法
学会用勾股定理进行简单的计算
学习难点
用面积法证明勾股定理
章节
勾股定理的认识
一
勾股定理的猜想
二
勾股定理的证明
三
勾股定理的应用
四
随堂小测
五
课堂小结
六
相传2500年前,古希腊著名的数学家毕达哥拉斯,经常从生活中寻找一些数学问题,有一次,他到朋友家做客,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
情景引入
返回
拼图
A
B
C
合作探究
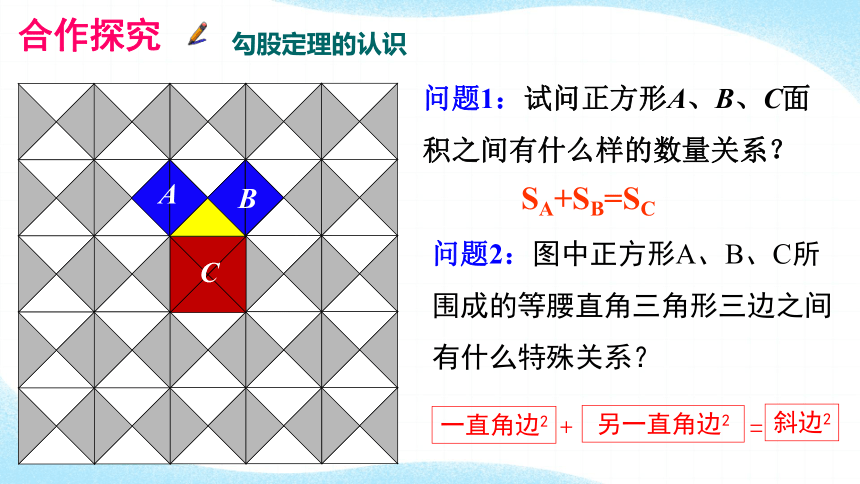
问题1:试问正方形A、B、C面积之间有什么样的数量关系?
A
B
C
SA+SB=SC
问题2:图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
勾股定理的认识
一直角边2
另一直角边2
斜边2
+
=
合作探究
勾股定理的认识
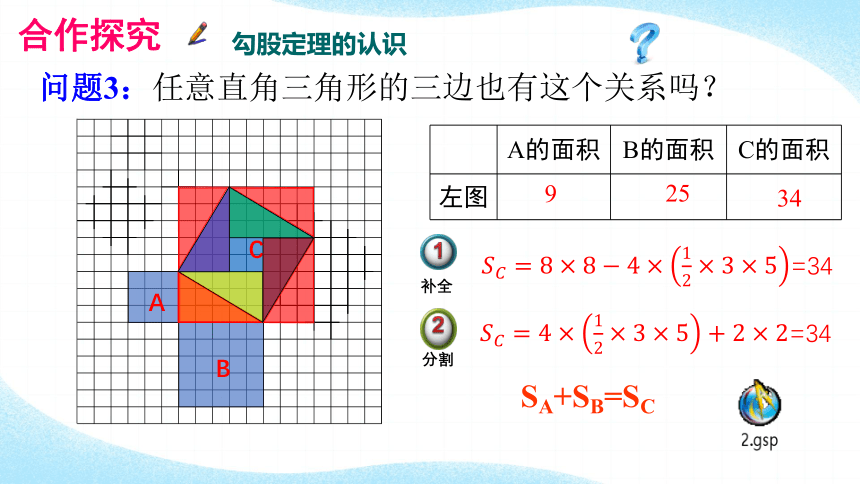
问题3:任意直角三角形的三边也有这个关系吗?
A
B
C
1
2
分割
补全
A的面积 B的面积 C的面积
左图
9
34
25
=34
=34
SA+SB=SC
合作探究
勾股定理的认识
合作探究
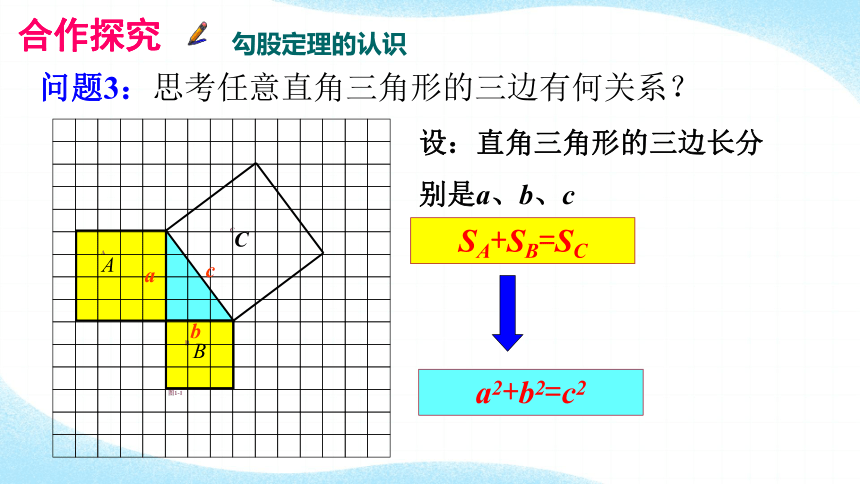
问题3:思考任意直角三角形的三边有何关系?
A
B
C
图1-1
A
B
C
a
b
c
设:直角三角形的三边长分别是a、b、c
SA+SB=SC
a2+b2=c2
合作探究
勾股定理的猜想
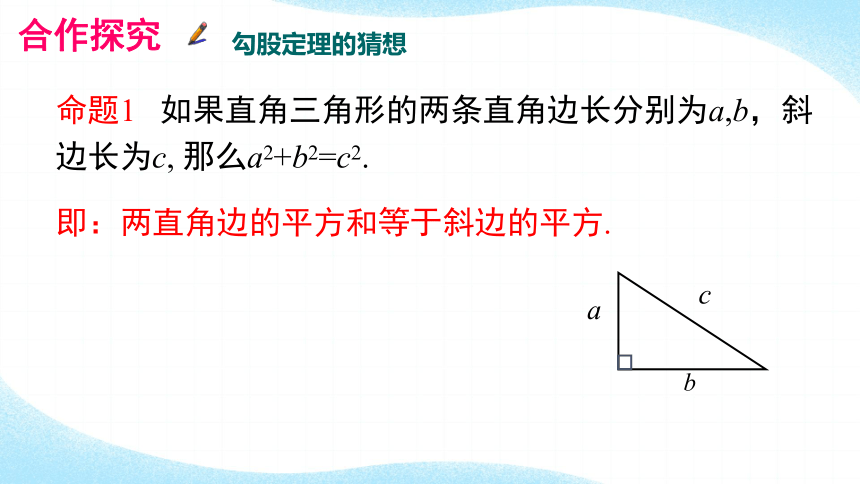
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c, 那么a2+b2=c2.
即:两直角边的平方和等于斜边的平方.
a
b
c
a
b
b
c
c
a
【材料准备】一个大正方形,边长为一个小正方形,边长为,按下图位置将两个正方形连在一起。
合作探究
勾股定理的证明
【活动要求】将这个图形分割成四个全等的直角三角形和一个正方形,再重新拼成右上角的图案。
a
b
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
合作探究
勾股定理的证明
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
(a、b、c为正数)
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
归纳总结
学以致用
勾股定理的应用
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
学以致用
勾股定理的应用
练习:在中,,,,则( )
A.4 B.3 C.2 D.1
【详解】
解:∵中,∠C=90°,且AB=5,BC=3,
∴AC==4.
故选:A.
A
学以致用
勾股定理的应用
变式: 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易漏解.
归纳
学以致用
勾股定理的应用
例2:(勾股树)如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形的边长分别是12,16,9,12,求最大正方形面积。
灰的面积+小灰的面积
大灰的面积=
小灰的面积=
学以致用
勾股定理的应用
s3
练习:已知求的值。
解:
方法归纳:
最大的正方形面积=其余小正方形的面积之和。
学以致用
勾股定理的应用
例3 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
归纳
随堂小测
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
随堂小测
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
17
5
74或24
作业来了:
1、在中,.
①若,,则 ;
②若,,则 ;
③若,,则 ;
④若,,则 。
2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为( )
3、如图,是某校的长方形水泥操场,如果一学生要从A角走到C角,至少要走( )
A、140米 B、100米 C、120米 D、90米
4、如图,正方形A的面积是144,正方形B的面积是169,则正方形C的边长是( )
A、25 B、100 C、313 D、5
同学们,再见
人教版八年级数学下册
第17章 勾股定理
17.1 勾股定理 第一课时
学习目标
1、经历勾股定理的探究过程,了解关于勾股定理的文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想。
2、培养在实际生活中发现问题总结规律的意识和能力。
学习重点
理解勾股定理的证明方法
学会用勾股定理进行简单的计算
学习难点
用面积法证明勾股定理
章节
勾股定理的认识
一
勾股定理的猜想
二
勾股定理的证明
三
勾股定理的应用
四
随堂小测
五
课堂小结
六
相传2500年前,古希腊著名的数学家毕达哥拉斯,经常从生活中寻找一些数学问题,有一次,他到朋友家做客,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系.
情景引入
返回
拼图
A
B
C
合作探究
问题1:试问正方形A、B、C面积之间有什么样的数量关系?
A
B
C
SA+SB=SC
问题2:图中正方形A、B、C所围成的等腰直角三角形三边之间有什么特殊关系?
勾股定理的认识
一直角边2
另一直角边2
斜边2
+
=
合作探究
勾股定理的认识
问题3:任意直角三角形的三边也有这个关系吗?
A
B
C
1
2
分割
补全
A的面积 B的面积 C的面积
左图
9
34
25
=34
=34
SA+SB=SC
合作探究
勾股定理的认识
合作探究
问题3:思考任意直角三角形的三边有何关系?
A
B
C
图1-1
A
B
C
a
b
c
设:直角三角形的三边长分别是a、b、c
SA+SB=SC
a2+b2=c2
合作探究
勾股定理的猜想
命题1 如果直角三角形的两条直角边长分别为a,b,斜边长为c, 那么a2+b2=c2.
即:两直角边的平方和等于斜边的平方.
a
b
c
a
b
b
c
c
a
【材料准备】一个大正方形,边长为一个小正方形,边长为,按下图位置将两个正方形连在一起。
合作探究
勾股定理的证明
【活动要求】将这个图形分割成四个全等的直角三角形和一个正方形,再重新拼成右上角的图案。
a
b
a
b
c
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
赵爽弦图
b-a
证明:
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽.
合作探究
勾股定理的证明
在我国又称商高定理,在外国则叫毕达哥拉斯定理,或百牛定理.
(a、b、c为正数)
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么a2+b2=c2.
公式变形:
勾股定理
a
b
c
归纳总结
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
勾2+股2=弦2
小贴士
归纳总结
学以致用
勾股定理的应用
例1 如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
学以致用
勾股定理的应用
练习:在中,,,,则( )
A.4 B.3 C.2 D.1
【详解】
解:∵中,∠C=90°,且AB=5,BC=3,
∴AC==4.
故选:A.
A
学以致用
勾股定理的应用
变式: 在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
图
图
当直角三角形中所给的两条边没有指明是斜边或直角边时,其中一较长边可能是直角边,也可能是斜边,这种情况下一定要进行分类讨论,否则容易漏解.
归纳
学以致用
勾股定理的应用
例2:(勾股树)如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形的边长分别是12,16,9,12,求最大正方形面积。
灰的面积+小灰的面积
大灰的面积=
小灰的面积=
学以致用
勾股定理的应用
s3
练习:已知求的值。
解:
方法归纳:
最大的正方形面积=其余小正方形的面积之和。
学以致用
勾股定理的应用
例3 已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
解:由勾股定理可得
AB2=AC2+BC2=25,
即 AB=5.
根据三角形面积公式,
∴ AC×BC= AB×CD.
∴ CD= .
A
D
B
C
3
4
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,它常与勾股定理联合使用.
归纳
随堂小测
1.下列说法中,正确的是 ( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36 cm
随堂小测
3.在△ABC中,∠C=90°.
(1)若a=15,b=8,则c= .
(2)若c=13,b=12,则a= .
4.若直角三角形中,有两边长是5和7,则第三边长
的平方为_________.
17
5
74或24
作业来了:
1、在中,.
①若,,则 ;
②若,,则 ;
③若,,则 ;
④若,,则 。
2、已知直角三角形的两边长分别为3cm和5cm,则第三边长为( )
3、如图,是某校的长方形水泥操场,如果一学生要从A角走到C角,至少要走( )
A、140米 B、100米 C、120米 D、90米
4、如图,正方形A的面积是144,正方形B的面积是169,则正方形C的边长是( )
A、25 B、100 C、313 D、5
同学们,再见
