人教版九年级下册数学第二十六章反比例函数 单元测试(含答案)
文档属性
| 名称 | 人教版九年级下册数学第二十六章反比例函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览

文档简介
第二十六章反比例函数(单元测试) 九年级下册数学人教版
一、单选题
1.下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
2.下列函数中,是反比例函数的是( )
A.y=x B.y=-2x+3 C.y=- D.y=-
3.若反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
4.一次函数y=mx+n的图像与反比例函数y=的图像交于点A、B,其中点A、B的坐标为A(-,-2m)、B(m,1),则△OAB的面积( )
A.3 B. C. D.
5.已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(-2,3) C.(3,0) D.(-3,0)
6.反比例函数与一次函数的图形有一个交点,则的值为( )
A.1 B.2 C. D.
7.某市煤气公司要在地下修建一个容积为立方米的圆柱形煤气储存室,记储存室的底面半径为r米,高为h米,底面积为S平方米,当h,r在一定范围内变化时,S随h,r的变化而变化,则S与h,S与r满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
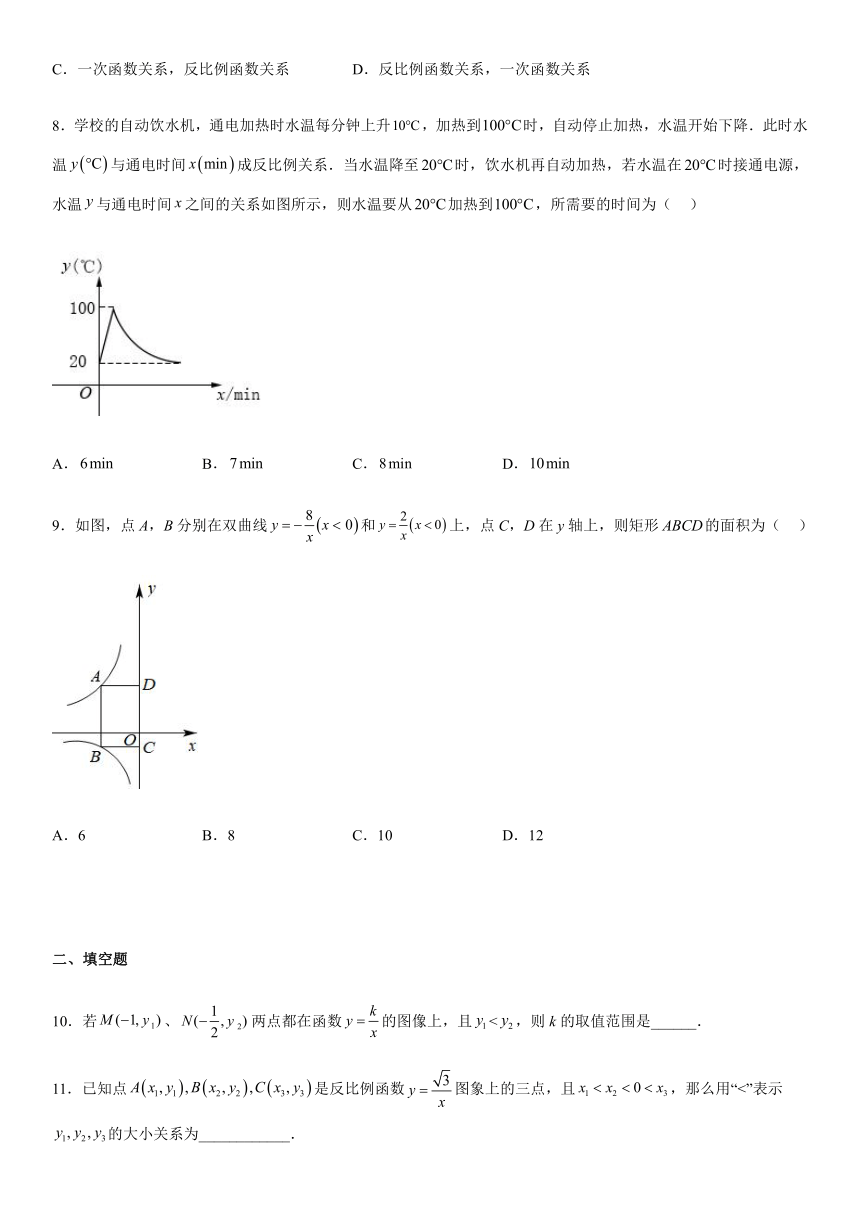
8.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
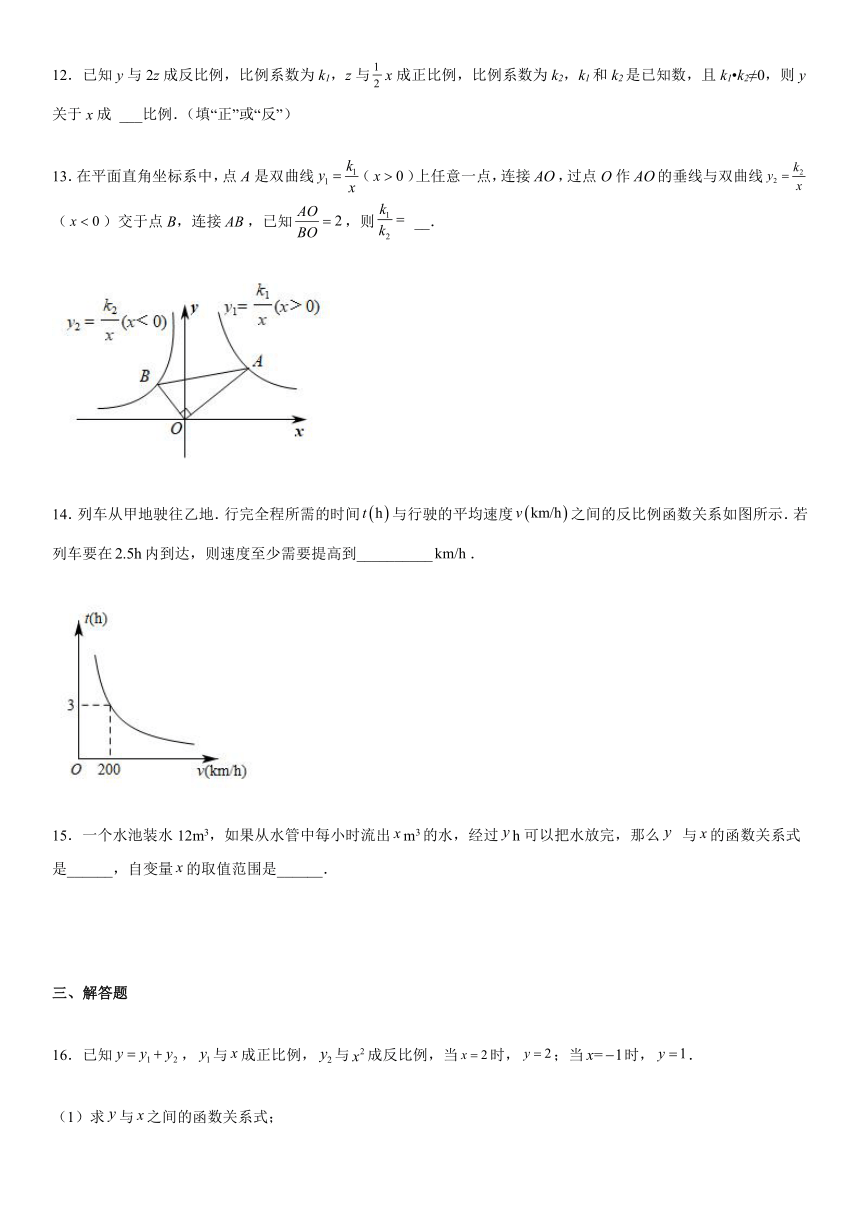
9.如图,点A,B分别在双曲线和上,点C,D在y轴上,则矩形的面积为( )
A.6 B.8 C.10 D.12
二、填空题
10.若、两点都在函数的图像上,且<,则k的取值范围是______.
11.已知点是反比例函数图象上的三点,且,那么用“<”表示的大小关系为____________.
12.已知y与2z成反比例,比例系数为k1,z与x成正比例,比例系数为k2,k1和k2是已知数,且k1 k2≠0,则y关于x成 ___比例.(填“正”或“反”)
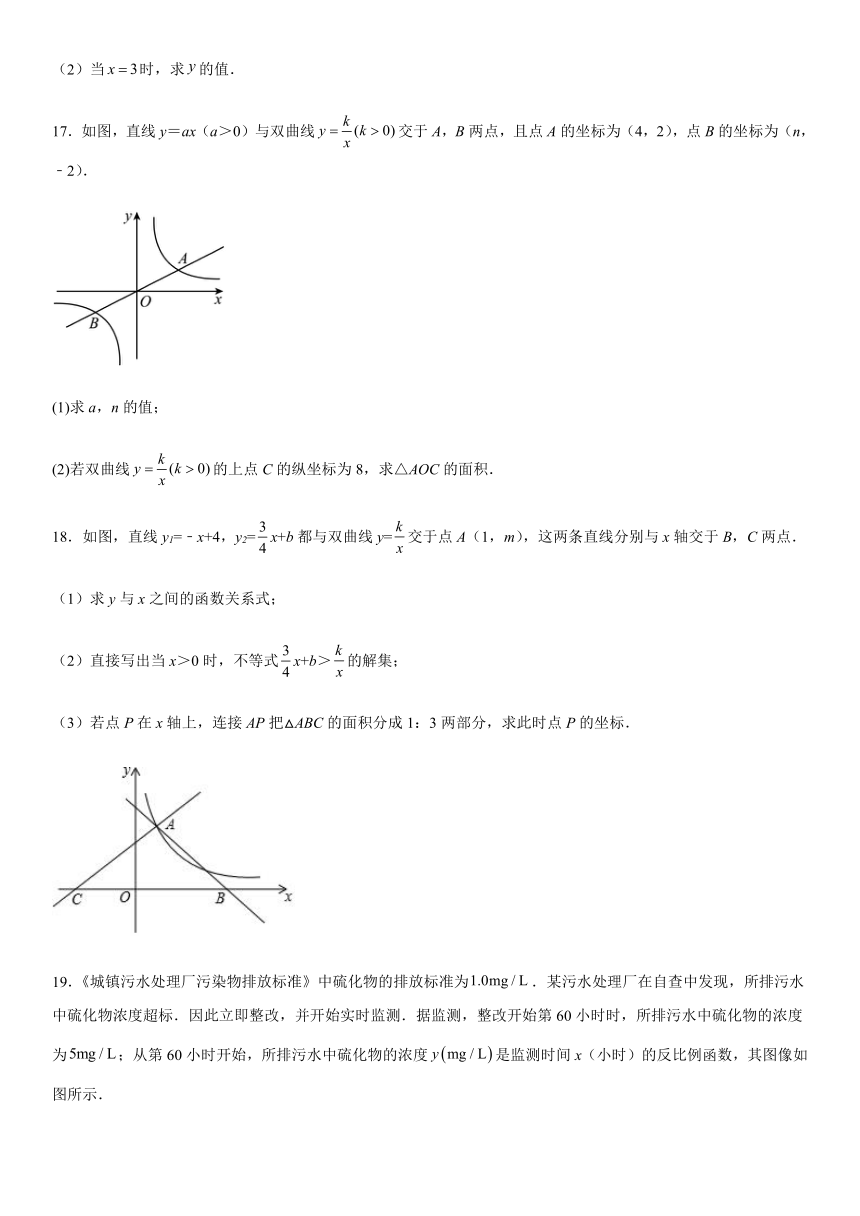
13.在平面直角坐标系中,点A是双曲线()上任意一点,连接,过点O作的垂线与双曲线()交于点B,连接,已知,则 __.
14.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
15.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
三、解答题
16.已知,与成正比例,与成反比例,当时,;当时,.
(1)求与之间的函数关系式;
(2)当时,求的值.
17.如图,直线y=ax(a>0)与双曲线交于A,B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线的上点C的纵坐标为8,求△AOC的面积.
18.如图,直线y1=﹣x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式x+b>的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.
19.《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标.因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图像如图所示.
(1)求y与x之间的函数关系式;
(2)按规定所排污水中疏化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少要多少小时?
20.如图,一次函数y=k1x﹣4的图象与反比例函数y(x>0)的图象相交于A(3,﹣6),并与x轴交于点B,点D是线段AB上一点,连结OD、OA,且S△BOD:S△BOA=1:3.
(1)求一次函数与反比例函数解析式;
(2)求点D的坐标;
(3)若将△BOD绕点O逆时针旋转,得到△B'OD',其中点D'落在x轴的正半轴上,判断点B'是否落在反比例函数y(x>0)图象上,并说明理由.
21.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地,边的长不超过墙的长度,在边上开设宽为1m的门(门不需要消耗篱笆).设的长为(m),的长为(m).
(1)求关于的函数表达式.
(2)若围成矩形劳动基地三边的篱笆总长为10m,求和的长度
(3)若和的长都是整数(单位:m),且围成矩形劳动基地三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
22.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
参考答案:
1.C
2.C
3.C
4.D
5.B
6.C
7.B
8.C
9.C
10.k<0
11.
12.反
13.
14.240
15. >0
16.(1);(2)
17.(1),
(2)15
18.(1);(2)x>1;(3)P(﹣,0)或(,0)
19.(1)
(2)375小时
20.(1)一次函数的解析式为y=-x-4,反比例函数的解析式为y=-;
(2)D(-3,-2);
(3)点B'不在函数y=-的图象上
21.(1)
(2)
(3)或
22.(1);(2);(3)
一、单选题
1.下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
2.下列函数中,是反比例函数的是( )
A.y=x B.y=-2x+3 C.y=- D.y=-
3.若反比例函数的图象经过点,则它的图象也一定经过的点是( )
A. B. C. D.
4.一次函数y=mx+n的图像与反比例函数y=的图像交于点A、B,其中点A、B的坐标为A(-,-2m)、B(m,1),则△OAB的面积( )
A.3 B. C. D.
5.已知反比例函数y=(k≠0),且在各自象限内,y随x的增大而增大,则下列点可能在这个函数图象上的为( )
A.(2,3) B.(-2,3) C.(3,0) D.(-3,0)
6.反比例函数与一次函数的图形有一个交点,则的值为( )
A.1 B.2 C. D.
7.某市煤气公司要在地下修建一个容积为立方米的圆柱形煤气储存室,记储存室的底面半径为r米,高为h米,底面积为S平方米,当h,r在一定范围内变化时,S随h,r的变化而变化,则S与h,S与r满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
8.学校的自动饮水机,通电加热时水温每分钟上升,加热到时,自动停止加热,水温开始下降.此时水温与通电时间成反比例关系.当水温降至时,饮水机再自动加热,若水温在时接通电源,水温与通电时间之间的关系如图所示,则水温要从加热到,所需要的时间为( )
A. B. C. D.
9.如图,点A,B分别在双曲线和上,点C,D在y轴上,则矩形的面积为( )
A.6 B.8 C.10 D.12
二、填空题
10.若、两点都在函数的图像上,且<,则k的取值范围是______.
11.已知点是反比例函数图象上的三点,且,那么用“<”表示的大小关系为____________.
12.已知y与2z成反比例,比例系数为k1,z与x成正比例,比例系数为k2,k1和k2是已知数,且k1 k2≠0,则y关于x成 ___比例.(填“正”或“反”)
13.在平面直角坐标系中,点A是双曲线()上任意一点,连接,过点O作的垂线与双曲线()交于点B,连接,已知,则 __.
14.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
15.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
三、解答题
16.已知,与成正比例,与成反比例,当时,;当时,.
(1)求与之间的函数关系式;
(2)当时,求的值.
17.如图,直线y=ax(a>0)与双曲线交于A,B两点,且点A的坐标为(4,2),点B的坐标为(n,﹣2).
(1)求a,n的值;
(2)若双曲线的上点C的纵坐标为8,求△AOC的面积.
18.如图,直线y1=﹣x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式x+b>的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.
19.《城镇污水处理厂污染物排放标准》中硫化物的排放标准为.某污水处理厂在自查中发现,所排污水中硫化物浓度超标.因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为;从第60小时开始,所排污水中硫化物的浓度是监测时间x(小时)的反比例函数,其图像如图所示.
(1)求y与x之间的函数关系式;
(2)按规定所排污水中疏化物的浓度不超过时,才能解除实时监测,此次整改实时监测的时间至少要多少小时?
20.如图,一次函数y=k1x﹣4的图象与反比例函数y(x>0)的图象相交于A(3,﹣6),并与x轴交于点B,点D是线段AB上一点,连结OD、OA,且S△BOD:S△BOA=1:3.
(1)求一次函数与反比例函数解析式;
(2)求点D的坐标;
(3)若将△BOD绕点O逆时针旋转,得到△B'OD',其中点D'落在x轴的正半轴上,判断点B'是否落在反比例函数y(x>0)图象上,并说明理由.
21.如图,某校劳动小组计划利用已有的一堵长为6m的墙,用篱笆围成一个面积为的矩形劳动基地,边的长不超过墙的长度,在边上开设宽为1m的门(门不需要消耗篱笆).设的长为(m),的长为(m).
(1)求关于的函数表达式.
(2)若围成矩形劳动基地三边的篱笆总长为10m,求和的长度
(3)若和的长都是整数(单位:m),且围成矩形劳动基地三边的篱笆总长小于10m,请直接写出所有满足条件的围建方案.
22.如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数于点B,已知.
(1)求直线的解析式;
(2)求反比例函数的解析式;
(3)点D为反比例函数上一动点,连接交y轴于点E,当E为中点时,求的面积.
参考答案:
1.C
2.C
3.C
4.D
5.B
6.C
7.B
8.C
9.C
10.k<0
11.
12.反
13.
14.240
15. >0
16.(1);(2)
17.(1),
(2)15
18.(1);(2)x>1;(3)P(﹣,0)或(,0)
19.(1)
(2)375小时
20.(1)一次函数的解析式为y=-x-4,反比例函数的解析式为y=-;
(2)D(-3,-2);
(3)点B'不在函数y=-的图象上
21.(1)
(2)
(3)或
22.(1);(2);(3)
