运河初级中学七年级上《第一章我们与数学同行》导学案
文档属性
| 名称 | 运河初级中学七年级上《第一章我们与数学同行》导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 255.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-09-21 17:01:52 | ||
图片预览



文档简介
运河初级中学“学讲计划”导学案
1.1生活 数学
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.通过生活中常见的数字、图形的观察,思考感受生活中处处有数学。
2.乐于接触社会环境中的数字、图形信息,知道数学是我们表达和交流的工具。
【自主感知】
1.看看你父母的身份证,你从中能获得哪些信息?
2.找找你乘车的车票,你从中又能获得哪些信息?
3.以上两个事例说明我们的生活和 是分不开的.这样的例子你还能举出哪些?
4. 想想我们的交通工具的车轮、奥林匹克的五环旗、2008北京申奥的标志,2008北京奥运会的会徽、上海世博会的会标等生活当中的物体形状
你会觉得我们的生活和 是分不开的,这样的例子你还能举出哪些?
【展示交流】
例1 某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差多少?
例2 2008年第二十九届奥林匹克运动会在北京举办,会徽“中国印、舞动的北京”由印形部分、“Bei jing 2008”字样和奥林匹克五环组成,奥林匹克五环象征五大洲的团结,体现“和平、友谊、进步”的奥林匹克宗旨。你能说出印形的意义吗?
【拓展延伸】
1.运河中学举行校园歌手大赛,7位评委给某选手的评分如下表。计分方法是:去掉一个最高分,去掉一个最低分,其余分数的平均分作为该选手的最后得分,则该选手的最后得分为( )
评委 1 2 3 4 5 6 7
得分 9.8 9.5 9.7 9.8 9.4 9.5 9.4
A.9.59 B.9.58 C.9.57 D.9.56
2.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆最多把平面分成1×2+2=4个部分,3个圆最多把平面分成2×3+2=8个部分,4个圆最多把平面分成3×4+2=14个部分,那么10个圆把平面分成多少个部分?
【盘点收获】
1.本节课我们探究的主要内容是:
2.给我们的主要感受是:
3.探究一些规律性的东西时,我们采用的是 的方法
4.你还有哪些独到的感悟或体会呢?
【自我检测】
1.猜谜语:
(1)数字虽小却在百万之上(打一数字)
(2)2、4、6、8、10(打一成语)
(3)从严判刑(打一数字名词)
三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
2.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的最多奖励有多少项?
3.小华每天起床后要做的事情有穿衣(4分钟)、整理床(3分钟)、洗脸梳头(5分钟)、上厕所(5分钟)、烧饭(20分钟)、吃早饭(12分钟),完成这些工作共需49分钟,你认为最合理的安排应是多少分钟?
4.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变。有关数据如下表所示:
(1)该风景区认为:调整前后这5个景点门票的平均收费不变,因此平均日总收入持平。问风景区是怎样计算的?
(2)游客认为:调整前后风景区的平均日总收入相对于调价前增加了9.4%,问游客是怎样计算的?
(3)你认为风景区和游客的说法,哪一种较能反映整体实际?
景点 A B C D E
原价(元) 10 10 15 20 25
现价(元) 5 5 15 25 30
平均日游客(千人) 1 1 2 3 2
运河初级中学“学讲计划”导学案
1.2活动 思考
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.在观察、实验、操作、猜想和归纳等数学活动中学会思考
2.能收集、选择、处理数字信息,作出合理的推断或大胆的猜想
【自主感知】
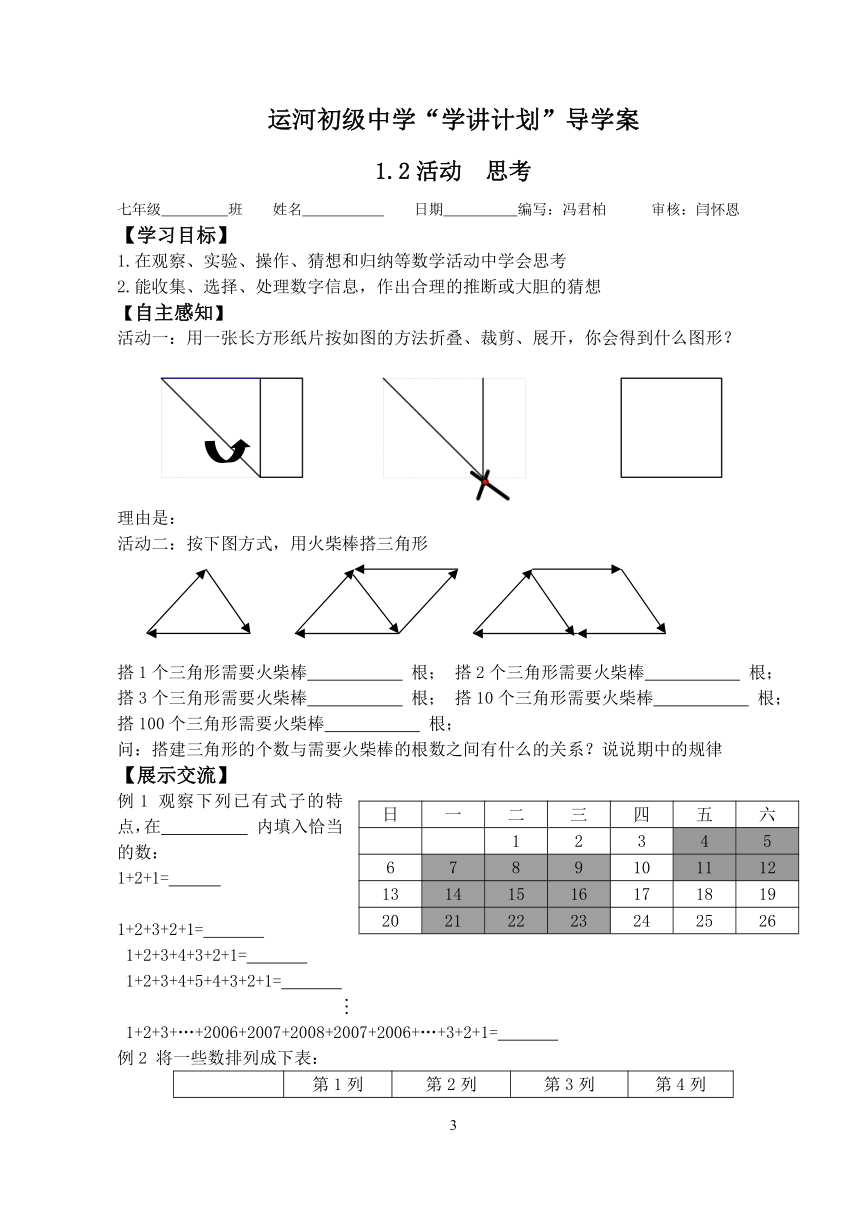
活动一:用一张长方形纸片按如图的方法折叠、裁剪、展开,你会得到什么图形?
理由是:
活动二:按下图方式,用火柴棒搭三角形
搭1个三角形需要火柴棒 根; 搭2个三角形需要火柴棒 根;
搭3个三角形需要火柴棒 根; 搭10个三角形需要火柴棒 根;
搭100个三角形需要火柴棒 根;
问:搭建三角形的个数与需要火柴棒的根数之间有什么的关系?说说期中的规律
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
【展示交流】
例1 观察下列已有式子的特点,在 内填入恰当的数:
1+2+1=
1+2+3+2+1=
1+2+3+4+3+2+1=
1+2+3+4+5+4+3+2+1=
1+2+3+…+2006+2007+2008+2007+2006+…+3+2+1=
例2 将一些数排列成下表:
第1列 第2列 第3列 第4列
第1行 1 4 5 10
第2行 4 8 10 12
第3行 9 12 15 14
试探索:(1)第10行第2列的数是多少?
(2)81所在的行和列分别是多少?
(3)100所在的行和列分别是多少?
【盘点收获】
1.本节课主要内容是探究数式、图形、表格所体现的
2.主要的探求方法是:
3.在数学实践中,规律的探求需要我们去大胆的
4.你还有哪些独到的见解和感悟呢?请写一写
【自我检测】
1.在 上填上适当的数:
(1)2,4,6, ,10,… (2)1,12,123,1234, ,123456,…
(3)1,3,6, ,15,21,… (4)1,1,2,3,5, ,13,21,…
2.日历表中某月所有星期六的日期数全加起来等于85,这个月的第一天是( )
A.星期三 B.星期四 C.星期五 D.星期六
3.将一张长方形的纸对折,如图,可得到一条折痕(图中虚线),连续对折,对折时每次折痕与上次折痕保持平行,连续对折三次后,可以得到7条折痕;那么连续对折四次后,可以得到 条折痕;连续对折五次后,可以得到 条折痕.
4.把一个长为9、宽为4的长方形分成两块,然后拼成一个正方形.(说说你的做法)
运河初级中学“学讲计划”导学案
2.1 正数与负数
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道正负数的概念,
2.会区分正负数
3.能用正负数表示具有相反意义的量.
【自主感知】
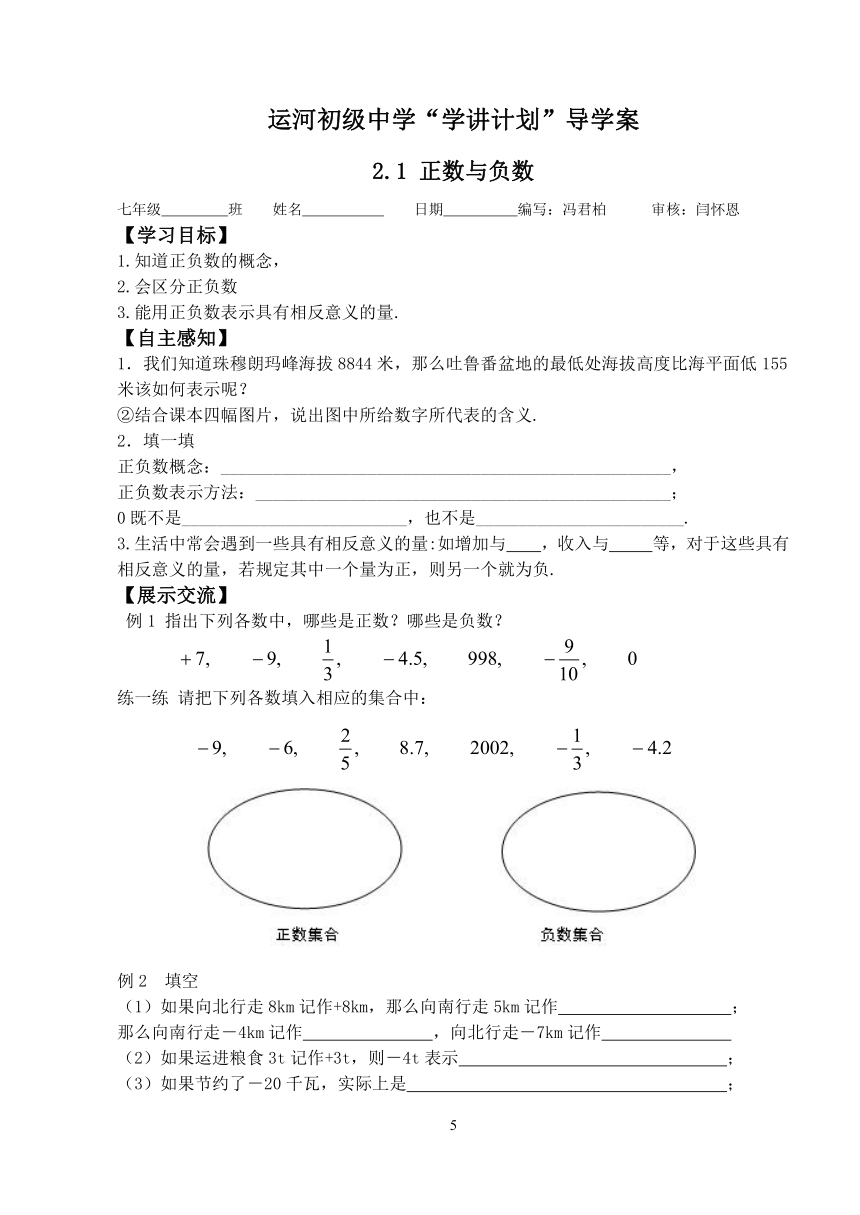
1.我们知道珠穆朗玛峰海拔8844米,那么吐鲁番盆地的最低处海拔高度比海平面低155米该如何表示呢?
②结合课本四幅图片,说出图中所给数字所代表的含义.
2.填一填
正负数概念:____________________________________________________,
正负数表示方法:________________________________________________;
0既不是__________________________,也不是________________________.
3.生活中常会遇到一些具有相反意义的量:如增加与 ,收入与 等,对于这些具有相反意义的量,若规定其中一个量为正,则另一个就为负.
【展示交流】
例1 指出下列各数中,哪些是正数?哪些是负数?
练一练 请把下列各数填入相应的集合中:
例2 填空
(1)如果向北行走8km记作+8km,那么向南行走5km记作 ;
那么向南行走-4km记作 ,向北行走-7km记作
(2)如果运进粮食3t记作+3t,则-4t表示 ;
(3)如果节约了-20千瓦,实际上是 ;
(4)如果负一场得-1分,实际上是 .
练一练:
(1)如果买入大米200kg记作+200kg,则卖出120kg大米记作
(2)如果-50元表示支出50元,那么+40元表示 ;
(3)太平洋最深处的马里亚纳海沟低于海平面11034m,它的海拔高度可以表示为 ;
【拓展延伸】
1.下表列出了几个城市与北京的时差(正数表示同一时刻比北京早的时数),如果现在是北京时间8:30.
城市 东京 纽约 巴黎 芝加哥
时差 +1 -13 -7 -14
⑴东京时间是多少 纽约、芝加哥的时间是多少
⑵小刚现在给远在巴黎的叔叔打电话,你认为合适吗
【盘点收获】
1.正数实质上是指 的数;
负数实质上是指 的数
2.一个数的前面带有正号一定是正数吗?一个数的前面带有负号一定是负数吗?
你的理由是
3.具有相反意义的量必须满足的条件是
①
②
【自我检测】
1.任举4个正数: ;任举4个负数: .
2.把下列各数填入相应的集合中:
正数集合:{ ,…}
负数集合:{ ,…}
3.如果时针顺时针方向旋转900记作-900,那么逆时针方向旋转600记作 ;
4.如果将低于警戒线水位0.27m记作-0.27m,
那么+0.42m表示 ____
5.用正,负数表示下列问题中的量:
①某商场在“五一”期间购进空调390台,销售了295台;
②某日A股上涨1个百分点,B股下跌3个百分点.
6.中午12时,水位低于标准水位0.5米记作-0.5米,下午1时水位上涨了1米,下午5 时水位又上涨了0.5米,则
①下午1时的水位可记录为 ,下午5时的水位可记录为 .
②下午5时的水位比中午12时的水位高 米.
运河初级中学“学讲计划”导学案
2.2有理数与无理数
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道什么是整数和分数
2.能分清有理数与整数和分数之间的关系,能对有理数进行正确分类
3.知道什么是无理数,并能对一个数的归属做出正确判断.
【自主感知】
1.学校的图书馆馆藏书近20万册,可是图书管理员阿姨总能很快地将你要借的书找出来,你知道这是为什么吗
2.我们小学学过哪些数?是怎样分类的?现在我们引入了负数,还能否按原来的标准分类?若能,分分看;还有其他的标准吗?试一试
3.整数包括
分数包括
4.有理数就是 的统称;
实质上就是 的数
于此相反无理数就是 的数
例如
【展示交流】
例1 把下列各数填在相应集合内:
正数集合:{ ,…}
负数集合:{ ,…}
整数集合:{ ,…}
分数集合:{ ,…}
例2 把下列各数填在相应的大括号内:
,0,π,314,-,,,-0.55,8,1.121 221 2221…(相邻两个1之间依次多一个2),0.2111,201,999.
正数集合:{ }
负数集合:{ }
有理数集合:{ }
无理数集合:{ }
【拓展延伸】
1.下列说法中,正确的是( )
A.有理数都是有限小数 B.无限小数都是无理数
C.3.14是无理数 D.π是无理数
2.①正整数和负整数统称为整数.②-0.5既是分数,也是负数.③0只表示没有.④正数和负数统称为有理数.⑤一个数不是正数就是负数.⑥既不是正数也不是整数的有理数是负分数.以上的说法中正确的有
3.下列四项中,错误的是( )
A.存在最小的自然数 B.存在最小的正有理数
C.不存在最大的正有理数 D.不存在最大的负有理数
4.写出所有适合下列条件的数:
(1)不大于3的正整数: ;
(2)大于-5的负整数: ;
(3)大于-3且不大于4的整数: .
【盘点收获】
1.有理数有两个分类标准,分别是
有理数 有理数
2.有理数就是 的数;无理数就是 的数
3. 是数学中一个最重要的数学思想,因为这是我们正确认识事物的关键.
【自我检测】
1.判断正误:
(1)不循环小数是无理数( )
(2)一个有理数不是正数就是负数( )
(3)有理数不一定是有限小数( )
(4)分数中有有理数,也有无理数,如就是无理数( )
2.一m是一个有理数,则它一定是( )
A.负数 B.正数 C.负数或负数 D.负数、零或正数
3.下列说法正确的是( )
A.整数就是正整数和负整数 B.分数包括正分数和负分数
C.正数和负数统称为有理数 D.3.1415926不是有理数
4.关于0的说法正确的是( )
A.不是正数也不是负数 B.是正数 C.是负数 D是正整数
5.既不是正数也不是整数的有理数是( )
A.0和负分数 B.负分数 C.负整数和负分数 D.正整数和正分数
6.不小于-2.5而小于2.8的非负整数有( )
A.2个 B.3个 C.4个 D.5个
运河初级中学“学讲计划”导学案
2.3数轴(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.了解数轴的概念,知道数轴的三要素,会画数轴,
2.能将已知数用数轴上的点表示出来,能说出数轴上已知点表示的数.
【自主感知】
1.感知
温度计可以用来测量室内温度,你能读出它们的示数吗?你能在温度计上找出表示-5°C,-15°C的刻度吗?
2.像__________________________________________________的直线叫做数轴.
数轴的三要素:_____________ 、 _____________ 、_____________
【展示交流】
例1 判断下列数轴的画法是否正确,若不正确,请在右边指出错误原因
例2 如图,指出数轴上点A、B、C表示的数
例3 在数轴上画出表示下列各数的点
2,-1.5,0,-,1.5,-
【拓展延伸】
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.请利用数轴回答下列问题:
⑴ 在数轴上,到原点的距离为5的点有_______个,它们表示的数是______________;
⑵ 在数轴上,从表示2的点出发,先向右移动3个单位长度,再向左移动6个单位长度,最后的终点表示的数是_____________________
⑶ 在数轴上,点M表示数2,那么与点M相距4个单位的点表示的数是_____________
【盘点收获】
1.数轴就是具有 、 、 的一条直线.
2. 可以用数轴上的点来表示 ,表示正数的点都在原点的_________侧,表示负数的点都在原点的_________侧.
3. 也是数学中一个重要的数学思想,它可以起到“以形助数,以数助形”的作用.
【自我检测】
1.下列说法错误的是( )
A.规定了原点、正方向和长度的直线叫数轴
B.所有的有理数都可以用数轴上的点表示
C.数轴上的原点表示数0
D.数轴上表示一3.33的点在表示一3的点的左边
2.在数轴上,到原点距离5个单位长度,且在数轴右边的数是( )
A.-5 B.+5 C. D.15
3.数轴上离开原点个单位长度的点所表示的数是__________.
4.指出数轴上A、B、C、D、E表示的数.
5.小明家,学校,书店在同一笔直的东西走向大街上,一天小明从学校(记作O点)出发,向西走50m回家拿钱(记作A点),又从家向东走110m到书店(记作B点)买书,当他从书店向西走80m时(记作C点)遇到小伟.
⑴以学校(O点)为原点,向东为正方向建立数轴,并在数轴上表出A,B,C,O的位置.
⑵C点位于学校的哪个方向,离学校的距离是多少?
6.在数轴上的点A表示-3,现在把点A先向右移动7个单位,再向左移动4个单位,则到达终点所表示的数是什么?
7.数轴上的点A和点B所表示的数分别是-1,3,若要使点A表示的数是点B表示的数的2倍,保持B点不动,应将点A怎样移动?
运河初级中学“学讲计划”导学案
2.3数轴(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.进一步体会数轴上的点与有理数的对应关系,体会“数形结合”的思想方法。
2.能利用数轴比较有理数的大小,
【自主感知】
某日,北京,长春,江苏,黑龙江的最高气温分别是0°C,-2°C,5°C,-3°C
1 你能直观地知道哪个温度高哪个温度低吗?对温度计来说,越是向上温度越大还是越小?
② 在数轴上画出表示这些温度的点,你能得到什么结论?
结论:_____________________________________________________________________
___________________________________________________________________________
【展示交流】
例1 比较下列各组数的大小
⑴ 5和0 ⑵ -和0 ⑶ 2和-3 ⑷ -3,1.5和0
例2 比较下列各组数的大小
⑴ -3.5和-0.5 ⑵ -和-0.25
变式:比较下列各组数的大小
1 -1 -4 0 5 -2 -
步骤:
⑴
⑵
⑶
例3 在数轴上表示-2和1,并根据数轴指出大于-2而小于1的整数。
【拓展延伸】
1. 观察数轴,能否找出符合下列要求的数:
(1)最大的正整数和最小的正整数; (2)最大的负整数和最小的负整数;
(3)最大的整数和最小的整数; (4)最小的正分数和最大的负分数.
(5)最小的有理数和最大的有理数
2.在数轴上有三个点A、B、C分别表示一3、0、2,按要求回答
(1)将A向右移动6个单位后,三个点表示的数谁最大,是多少
(2)将C向左移动4个单位后,此时B点表示的数比C点的数大多少
(3)怎样移动A,B,C中的两个点,才能使这三个点表示的数相同 有几种方法
【盘点收获】
1.在数轴上的两个点中,右边的点表示的数 左边的点表示的数;正数 0;
小于0;正数大于 .利用这个性质可以比较两个有理数的大小.
2.数轴上点的平移所对应的数:
点向右平移几个单位,那么对应的数就在原来的基础上 (填“加上”或“减去)几;
向左平移几个单位,那么对应的数就在原来的基础上 (填“加上”或“减去”)几.
【自我检测】
1.填空
(1)不小于-3的负整数有哪些?
(2)比-2小4的数是什么数?
(3)-3比-9大多少?
(4)比-3小5的数是 ;比-3大5的数是
(5)-2和6的正中间的数是什么?
2.从数轴上观察,不小于-3而且不超过4的正整数有( )
A.5个 B.6个 C.7个 D.8个
3.下列说法正确的是( )
A、0是最小的有理数
B、若有理数m>n,则数轴上表示m的点一定在表示n的点的左边
C、一个有理数在数轴上表示的点离原点越远,这个有理数就越大
D、既没有最小的正数,也没有最大的负数。
4.点M从数轴上原点开始,先向左移动5个单位长度,再向右移动2个单位长度,此时点A所表示的数是
5.将有理数一4,5、3、0、一1、1、一3数轴上表示出来,并用“<”把这些数从小到大的顺序连接起来.
【探究与思考】(这三个小题仅供同学们课下研究)
1.一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2各单位,第3次向右跳3个单位,第4次向左跳4个单位……依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是__________个单位。
2.1路公交车在笔直的淮海路上来回奔跑,起点站是A,由A向东走5站是终点站B,回头向西走3个站,这时公共汽车在A站的何位置 若由A→B→A算走一趟,每站间路程是S千米,每千米耗油m升,则该公共汽车1天10趟耗油多少升
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道什么是有理数的绝对值以及表示方法,
2.能求一个有理数的绝对值并进行有关的简单计算,
3.会比较两个负数的大小.?
【自主感知】
1.一天,汽车司机张师傅从车站出发,沿东西方向行驶,规定向东为正,若向东行驶3千米,记作_____ ;若向西行驶2千米,记作_____ .若每千米耗油10升,则向东行3千米,耗油量是 ______ ,向西行2千米,耗油量是 ______ .
2.假设把汽车行的路想像成数轴,将车站定为原点,向东行驶3千米到达A点,向西行驶2千米到达B点.数轴上点A与原点的距离是____个单位长度,点B与原点的距离是_____个单位长度.
定义: 叫做这个数的绝对值.绝对值的符号:“ ”
注意:1.任何有理数的绝对值都是 数
2.绝对值最小的数是 ; (填“有”或“无”)绝对值最大的数
【展示交流】
例1 在数轴上画出表示下列各数的点:,并写出它们的绝对值.
例2 求下列各组数的绝对值,并分别比较它们绝对值的大小:
(1)-3.5与4 (2)-3与-6
思考:对第(2)题的解答你发现比较两个负数的大小有怎样的规律呢?
规律:
【拓展延伸】
1.某厂生产闹钟,检验时,比标准时间多的记为正数,比标准时间少的记为负数,请根据下表,选出最准确的闹钟.
1 2 3 4 5
+2s -3.5s 6s +7s -4s
误差不超过5秒的为合格品,否则为次品,问有几台合格?
2.,计算的值
【盘点收获】
1.数的绝对值实质上是 的距离,所以一个数
的绝对值不能是负数,也就是说一个数的绝对值一定是 数.
2.两个负数比较,绝对值 的反而小.
【自我检测】
1.计算
|-3|= , ||= ,
|-0.4|= , |0|= __
|9|= __ , |-2|=
2.用“<”把|-3|、|-0.4|及|-2|连接起来.
3.填空:
(1)绝对值小于3的所有整数是________________,非正整数是 ____
(2)若|x|=6,则x =
(3)在数轴上A表示-,点B表示,则点 离原点的距离近些.
4.计算:
(1)|—3|×|—6.2| (2)|—5| + |—2.49|
(3)|—|—|| (4) |—|÷||
5.某车间生产一批圆形零件,从中抽取8件进行检验,比规定直径长的毫米数记为正数,比规定直径短的毫米数记为负数,检查记录如下:
1 2 3 4 5 6 7 8
+0.3 -0.2 -0.3 +0.4 0 -0.1 -0.5 +0.3
指出第几个零件最标准?最接近标准的是哪个零件?误差最大的是哪个零件?
6.(1),求的值.
(2)已知| a+2 | + (b-3)2 =0,求a+b的值.
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数的相反数概念及表示方法,
2.会求一个有理数的相反数以及有关的简单计算
【自主感知】
1.数轴上到原点的距离是3的点有几个 它们到原点的距离各是多少 它们之间还有什么关系
2.在数轴上到原点的距离是2.5的点有几个 它们到原点的距离各是多少 它们之间还有什么关系
3.观察下列各对有理数,你发现了什么?
5与-5 -2.5与2.5
定义:像5与-5 、-2.5与2.5 …这样 、 的两个数,叫做互为相反数,其中一个是另一个的________ (只有符号不同的两个数).
规定:零的相反数是零
注意:①正数的相反数是________;负数的相反数是________;0的相反数是_________.
②表示一个数的相反数,只要在这个数的前面添加一个“ ”号即可.
【展示交流】
例1 求出3、-4.5、0、的相反数(在一个数的前面添一个“-”,就表示这个数的相反数)
例2 化简:.
思考:对上题的解答可以看出,对于双重符号的化简问题有个规律,这个规律是
例3 求6、-6、0、 、 的绝对值,有什么发现
归纳:相反数的性质:
①__________________________________________
②__________________________________________
③__________________________________________
思考:一个数的绝对值与这个数本身或它的相反数有什么关系?
一个正数的绝对值是____ 一个负数的绝对值是______
0的绝对值是______
【拓展延伸】
(1) 绝对值不小于3的整数是什么?绝对值小于5的整数是什么?绝对值小于3的整数是否都小于绝对值小于5的整数?
(2)已知x是整数,且2.5<|x|<7,求x.
(3)已知点A,B分别为数轴上表示互为相反数的两个点,且A,B两点间的距离为5,其中A在B的左边,请你写出这两个点所表示的数.
【盘点收获】
1.本节课的知识点你认为有哪些?列举出来
【自我检测】
1.下列各组中互为相反数的是( )
A.一2与 B,|-2|与2 C.一2.5与|-2| D.-0.5与|-|
2.下列各数中互为相反数的是 ( )
A、与0.2 B、与-0.33 C、-2.25与 D、5与-(-5)
3.下列各对数中互为相反数的是 ( )
A.-(+3)和+(-3) B.-(-3)和+(-3) C.-(+3)和-3 D.+(-3)和-3
4.在-中,负数有( )
A.1个 B.2个 C.3个 D.4个
5.下列说法:① 如果a=-13,那么-a=13, ② 如果a=-1,那么-a=-1, ③ 如果a是非负数,那么-a是正数, ④如果a是负数,那么+1是正数, 其中正确的是 ( )
A ①③ B ①② C ②③ D ①④
5. 若,则是( )
A.0 B.正数 C.负数 D.负数或0
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会比较两个有理数的大小,
2.进一步感受数形结合等数学思想方法.
【自主感知】
一、回顾
1.什么叫绝对值?如何求一个数的绝对值?
2.什么叫相反数?互为相反数的两个数有什么性质?
4、填空:
(1)+|-2|=________ (2)-|+4|=________
(3)|+3.5|-|-2|=________ (4)-(-2.3)=_____
(5) +(-5)=________ (6)-|-4|=________
二、探究
1.两个有理数如何比较大小 数轴上两数如何比较?
结论
2.绝对值大的那个数数就一定大吗
思考:
(1)正数的绝对值大于0的绝对值,正数比0大吗?
(2)负数的绝对值大于0的绝对值,负数比0大吗?
(3)正数的绝对值就是它本身,绝对值大的正数大,绝对值小的正数小吗?
(4)负数的绝对值是它的相反数,绝对值大的负数大,绝对值小的负数小吗?
3、两个有理数的大小与这两个数的绝对值的大小有什么关系?
结论:
【展示交流】
例1 (1)比较-9.5与- 1.75的大小
(2)比较-与-(-2.9)的大小
例2 数a、b在数轴上的位置如图所示,则下列判断中,正确的是( )
A.a>-1 B.b>1 C.a<-1 D.b<0
例3 有理数、、在数轴上的位置如图,
判断正负,用“>”或“<”填空
-_0, - _0, +_0
【盘点收获】
1.两个有理数比较时,重点是同号比较,通正比较, 的大;同负比较, 的反而小.
2.两个数相减,大的减小的差 0;小的减大的差 0(填“大于”或“小于”)
【自我检测】
1.三个数-3、-4、0依次从小到大排列的顺序是 ( )
A.0<-4<-3 B.-3<-4<0
C.0<-4<-3 D.-4<-3<0
2.下面四个结论中,正确的是 ( )
A.= B.-2>0
C.-2< D. >0
3.比较大小:
(1)3 -7 (2)-5.3 -5.4
(3)- - (4)-|-0.4| -(-0. 4)
4.化简:
(1)-= (2)=
(3)= (4)=
5.飞机上升3000米,记作+3000米;又下降3000米,记作-3000米,那么飞机还是原来的高度
小明数学竞赛获奖,爸爸奖励50元,记作+50元;他很高兴,去书店买书,花了50元,记作-50元,那么他的剩余钱恰好为0
(1)+3000和-3000,+50和-50有什么关系?
(2)猜想两个数互为相反数,那么它们的和是多少?
(3)用你第(2)步的结论计算:字母a、b、c、d表示有理数,且a、b互为相反数,正数c的绝对值是2,d的相反数是-5,求a+b+c×d的值
运河初级中学“学讲计划”导学案
2.5 有理数的加法与减法(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.探索有理数加法法则,理解有理数的加法法则
2.能熟练进行有理数的加法运算
3.有初步的分类思想
【自主感知】
1.填一填
足球队甲、乙两队比赛,主场甲队4:1胜乙队,赢了3球,客场甲队1:3负乙队,输了2球,甲队两场比赛累计净胜球1个,你能把这个结果用算式表示出来吗?
你知道的比赛中胜负难料,两场比赛的结果还可能哪些情况呢?动动手填表:
赢球数 净胜球 算式
主场 客场
3 ‐2
‐3 2
3 2
‐3 ‐2
3 0
0 ‐3
你还能举出一些应用有理数加法的实际例子吗?
例如:第一天水位下降了5厘米,第二天水位上涨了8厘米,两天水位变化情况是上涨了3厘米.用算式表示这个结果。
算式:_______________________
2.讨论:两个有理数相加时,和的符号及绝对值怎样确定?你能找到有理数相加的一般方法吗?
有理数加法法则:
同号两数相加,__________________________________________________.
异号两数相加,_______________________________________;
一个数与0相加,__________________.
【展示交流】
例1 计算下列各题:
(1)(-180)+(+20) 2)(-15)+(-3)
(3)5+(-5) (4)0+(-2)
例2
某仓库原有粮食80吨,第一天运进粮食54吨,第二天又运出粮食32吨,现在仓库共有粮食多少吨?
思考:两个有理数相加,和一定比两个加数大吗?
【盘点收获】
1.有理数的加法运算主要搞清两个方面的问题
① ;② .
【自我检测】
一、选择
1.一个正数与一个负数的和是
A.正数 B.负数
C.零 D.以上三种情况都有可能
2.绝对值不大于3的所有整数的和为
A. 6 B. -6 C.±6 D.0
3.两个有理数的和
A.一定大于其中的一个加数 B.一定小于其中的一个加数
C.大小由两个加数符号决定 D.大小由两个加数的符号及绝对值而决定
二、判断
1.绝对值相等的两个数的和为0 ( )
2.若两个有理数的和为负数,则这两个数至少有一个是负数( )
3.如果某数比-5大2,则这个数的绝对值是3 ( )
三、填空题:
1. ⑴ (+3)+(+7)=______ ⑵ (+3)+(—8)=_______
⑶ (—12)+(—5)=_________ ⑷ (—37)+22 =_________
⑸ 0+(—19) =___________ ⑹ (—7)+ |—5 |=_________
2. 若 | m |= 2, | n | =5 ,且m>n, 则m+n =___________
四、计算;
⑴(+10)+(—4) ⑵(—15)+(—32) ⑶(—9)+ 0
五、列式解答
(1)一个数与-5的差为-8,求这个数
(2)一个数与9的差为-5,求这个数
六、土星表面夜间的平均气温为-150℃,白天的平均气温比夜间高27℃,那么白天的平均气温是多少?
七、潜水员原来在水下15米处,后来上浮了8米,又下潜了20米,这时他在什么位置?要求用加法解答。
运河初级中学“学讲计划”导学案
2.5 有理数的加法与减法(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.经历探索有理数加法运算律的过程,理解有理数的加法运算律的实质;
2.能运用加法运算率简化加法运算;
【自主感知】
一、算一算
情景1: 情景2:
3+(-5)=
(-5)+ 3 =
二、总结
上面两个情景中所使用的数学运算律是:
1.加法的交换律:
2.加法的结合律:
【展示交流】
例1 计算:
1.(-23)+(+58)+(-17) 2.(-2.8)+(-3.6)+(-1.5)+3.6
3.
思考:有理数的加法运算中,利用运算律,我们往往采取如下的策略
①
②
③
④
练习:计算:
1. (-11)+8+(-14) 2. (-4)+(-3)+(-4)+3
3. 4. 8+(-2)+(-4)+1+(-3)
5. 0.35+(-0.6)+0.25+(-5.4) 6.
【盘点收获】
谈谈在加法的运算中灵活性有哪些方面
【自我检测】
1.计算:
(1)(-3)+40+(-32)+(-8) (2)43+(-77)+27+(-43)
(3)18+(-16)+(-23)+16 (4)(-3)+(+7)+4+3+(-5)+(-4)
(5)5.6+(-0.9)+4.4+(-8.1) (6)
2.计算
1+(-2)+(-3)+4+5+(-6)+(-7)+8+……+2001+(-2002)+(-2003)+2004
3.求绝对值大于3且小于6的所有整数的和。
4.某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:(单位:千米)
⑴ 问收工时离出发点A多少千米?
⑵ 若该出租车每千米耗油0.3升,问从A地出发到收工共耗油多少升?
运河初级中学“学讲计划”导学案
2.5有理数的加法与减法(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.探索有理数减法法则的过程;
2.能熟练地进行有理数的减法运算;
3.体会转化的思想方法
【自主感知】
1.问题
一天的最高气温与最低气温的差叫做日温差。
如果某天的最高气温是5℃,最低气温是3℃,那么这天的日温差是多少(列式计算)
如果某天的最高气温是5℃,最低气温是-3℃,那么这天的日温差是多少(列式)
2.感知
猜想:有理数的减法法则:减去一个数等于
即表示成a-b=a+(-b).
验证:
(1)如果某天A地气温是3℃,B地气温是-5℃,A地比B地气温高多少?
3-(-5)=3+ ;
(2)如果某天A地气温是-3℃,B地气温是-5℃,A地比B地气温高多少?
(-3)-(-5)=(-3)+ ;
(2)如果某天A地气温是-3℃,B地气温是5℃,A地比B地气温高多少?
(-3)-5=(-3)+ ;
【展示交流】
例1 计算:
①15-(-7) ②(-8.5)-(-1.5)
③ 0-(-22) ④(+2)-(+8)
⑤(-4)-16 ⑥
练一练:口答
(1) 3 – 5 (2) 3 – (-5)
(3)(-3)– 5 (4)(-3) –(-5)
(5)–6 -(-6) (6)-7-0
(7)0 -(-7) (8)(-6)-6
(9)9 -(-11) (10) 6-(-6)
思考:在有理数范围内,差一定比被减数小吗
例2.求出数轴上两点之间的距离:
(1)表示数10的点与表示数4的点;
(2)表示数2的点与表示数-4的点;
(3)表示数-1的点与表示数-6的点。
思考:通过对例2的求解可以得出这样一个结论
求数轴上任意两点的距离只要求出两个点所对应的数的 的绝对值即可.
【拓展延伸】
(1)-13.75比少多少?
(2)从-1中减去-与-的和,差是多少?
【盘点收获】
1.有理数的减法法则:________________________________________
(其实质是将减法转化为___________)
2.数轴上两个点之间的距离就是这两个点表示的数的差的 .
【自我检测】
1.下列说法中正确的是( )
A.减去一个数,等于加上这个数.
B.零减去一个数,仍得这个数.
C.两个相反数相减是零.
D.在有理数减法中,被减数不一定比减数或差大.
2.下列计算中正确的是( )
A.(—3)-(—3)= —6 B . 0-(—5)=5
C.(—10)-(+7)= —3 D . | 6-4 |= —(6-4)
3.下列说法中正确的是( )
A.两数之差一定小于被减数.
B.减去一个负数,差一定大于被减数.
C.减去一个正数,差不一定小于被减数.
D.零减去任何数,差都是负数.
4.若不为0的两个数的差是正数,则一定是( )
A.被减数与减数均为正数,且被减数大于减数.
B.被减数与减数均为负数,且减数的绝对值大.
C.被减数为正数,减数为负数.
D.以上3种均可满足条件.
5.(1)(—2)+________=5; (—5)-________=2.
(2)0-4-(—5)-(—6)=___________.
(3)月球表面的温度中午是1010C,半夜是-153oC,则中午的温度比半夜高____.
(4)已知一个数加—3.6和为—0.36,则这个数为_____________.
(5)已知b < 0,则a,a-b,a+b从大到小排列________________.
运河初级中学“学讲计划”导学案
2.5有理数的加法与减法(4)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会进行有理数的加减混合运算
2.会计算省略加号和括号的有理数加减混合运算
【自主感知】
1.回顾
计算:
(1)7-(-4)+(-5) (2)-2-12+(-3)+8-(-6)
根据有理数的减法法则,有理数的加减混合运算可以统一为___________
2.新知
在把有理数加减混合运算统一为加法的算式中,负数前面的加号可以省略不写.
例如7+4+(-5)可以写成7+4-5,它表示7、4与(-5)的和.
计算:
(-4)+9-(-7)-13
解:原式=-4+9+(+7)+(-13) 减法转化为加法
=-4+9+7-13 省略加号的和
=-4-13+9+7 加法交换律
=-17+16 同号两数相加
=-1 异号两数相加
11-39.5+10-2.5-4+19
解:原式=11+10+19-39.5-2.5-4 加法交换律
=【(11+19)+10】+【(-39.5-2.5)-4】 加法结合律
=40-46 同号两数相加
=-6 异号两数相加
【展示交流】
例1 计算
(1)-3-5+4 (2)-26+43-24+13-46
练一练:计算
(1)7-(-6)-(-5) (2)-21-12+33+12-67
(3)5.4-2.3+1.5-4.2 (4)
例2 巡道员沿东西方向的铁路进行巡视维护。他从住地出发,先向东行走了7km,休息之后继续向东行走了3km;然后折返向西行走了11.5km.此时他在住地的什么方向?与住地的距离是多少?
【盘点收获】
1.有理数加减混合运算统一为有理数的_________运算
2.性质符号与运算符号的辨析
3.谈谈你对本节课的见解
【自我检测】
1.判断题
(1)运用加法交换律,得-7+3=-3+7. ( )
(2)-5-4=-9.( ) -5-4=-1.( )
(3)两个数相加,和一定大于任一个加数. ( )
(4)两数差一定小于被减数. ( )
(5)零减去一个数,仍得这个数. ( )
2.选择题
(1)把(+5)-(+3)-(-1)+(-5)写成省略括号的和的形式是 ( )
A.-5-3+1-5 B.5-3-1-5
C.5+3+1-5 D.5-3+1-5
(2)算式8-7+3-6正确的读法是 ( )
A.8、7、3、6的和 B.正8、负7、正3、负6的和
C.8减7加正3、减负6 D.8减7加3减6的和
(3)两个数相加,其和小于每个加数,那么这两个数( )
A.同为负数 B.异号 C.同为正数 D.零或负数
(4)甲数减去乙数的差与甲数比较,必为( )
A.差一定小于甲数 B.差不能大于甲数
C.差一定大于甲数 D.差的大小取决于乙是什么样的数
3.把下列各式写成省略括号的和的形式
(1)(-28)-(+12)-(-3)-(+6)
(2)(-25)+(-7)-(-15)-(-6)+(-11)-(-2)
4.计算下列各题
(1)(+17)-(-32)-(+23) (2)(+6)-(+12)+(+8.3)-(+7.4)
5.小虫从某点A出发,在一直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:厘米):+5,—3,+10,—8,—6,+12,—10.(1)小虫最后是否回到出发点A?
(2)小虫距离出发点最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则小虫一共得到多少粒芝麻?
运河初级中学“学讲计划”导学案
2.6 有理数乘法与除法(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数乘法的运算法则
2.会进行有理数的乘运算
【自主感知】
1.回答课本提出的问题
① ; ②
③ ; ④ .
2.如果我们把水位上升为正,下降为负;几天后记为正,几天前记为负,那么上面的四个问题你能否用有理数运算的式子来表达,试一试
① ; ②
③ ; ④ .
3.解决课本中的“想一想”
4.填写课本中的相关表格
5.总结有理数乘法法则
_____________________________________________________________________________
___________________________________________________________________________.
【展示交流】
例题1 计算:
(1) (- 4)×5; (2) (- 5) ×(-7)
思考:正确进行有理数的乘法运算要注意两个关键点,这两个关键点分别是
① ②
例2 计算;(1)2×(一3) × 5×(一1) (2)(一)××(一)×(一)
思考:对于两个以上的有理数相乘,仍然要注意两个关键点,不过在确定积的符号时,只须看 的个数即可;负因数的个数为 ,积为负;负因数的个数为偶数时,积为 .
【盘点收获】
1.有理数乘法法则:两数相乘,同号得 ,异号得 ,并把绝对值相乘,任何数同零相乘都得 .
2.几个不是0的有理数相乘,积的符号由 的个数决定,当负因数有奇数个时、积为 ,当负因数有 个时积为正.
【拓展延伸】
1.若规定,则 , .
2.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,……,
则
【自我检测】
1.(-4)×()的结果为 ( )
A.6 B.-6 C.2 D.-2
2.互为相反数的两数相乘,积为 ( )
A.正数 B.负数 C.0 D.负数或0
3.五个有理数相乘,积的符号为负,则负因数的个数有 ( )
A.1个 B.3个 C.5个 D.1个或3个或5个
4.计算:⑴ , ⑵ (+18) ×(-6)= ,
⑶ 0×()= , ⑷= .
5.计算下列各题:
(1) 3 ×(-5)×(-7)× 4 (2)15 ×(-17)×(-19)×0
(3) (4)
6.初一年级共100名学生,在一次数学测试中以90分为标准,超过的记为正,不足的记为负,成绩如下:
人数 10 20 5 14 12 18 10 4 9 6 2
成绩 -1 +3 -2 +1 +10 +2 0 -7 +7 -9 -12
请你算出这次考试的平均成绩。
运河初级中学“学讲计划”导学案
2.6有理数乘法与除法(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.熟记有理数的乘法法则
2.会运用乘法运算率简化乘法运算.
【自主感知】
1.算一算,看一看,想一想
第一组:
(1)3×4= ______ (2)4×3= ______
(3)(-3)×4= ______ (4)4×(-3)= ______
(5)3×(-4)= ______ (6)(-4)×3= ______
(7)(-3)×(-4)= _____ (8)(-4)×(-3)= ______
第二组:
(1)[(-3)×4]×0.5=_______ (-3)×(4×0.5)=_______
(2)[3×(-8)]×0.125=________ 3×[(-8)×0.125]=_______
第三组:
(1) _______ _______
(2)(-4)×(-3)+(-4)×5=______ (-4)×(-3+5)=_________
通过你的计算能得到什么结论?
2.计算
(1) ;(2) ;(3) .
像这样乘积为 的两个数,我们称为互为倒数,其中一个是另一个的倒数.
【展示交流】
例1 (1) (2)
思考:通过上两个题的计算,提醒我们在利用运算律时要注意什么呢?
例2(1)×(—8) (2)15×(—+)-24×(—)
思考:对于带分数的相关计算我们要注意什么呢?
【盘点收获】
1.乘法法交律:两个数相乘,交换因数位置,积不变,即:(用含有字母的式子表达)
2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相等,积不变,即:(用含有字母的式子表达)
3.乘法分配律:一个数同两个数的和相乘,等于把这个数分别同两个加数相乘,再把积相加.即:(用含有字母的式子表达)
【自我检测】
1.-的倒数是 ,倒数等于本身的数是
2.乘积为-1的数叫做互为负倒数,则-2的负倒数是( )
A.-1 B.- C. D.1
3.a、b互为相反数,c、d互为负倒数,则a十b+cd=
4.计算(-7.5)×(—)+(-7.5)×-(—7.5)×6=
5.利用分配律计算时,正确的方案可以是 ( )
A . B.
C . D .
6.计算:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
运河初级中学“学讲计划”导学案
2.6有理数乘法与除法(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会将有理数的除法转化成乘法
2.会进行有理数的乘除混合运算
【自主感知】
1.问题
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
这周每天上午8时的平均气温为多少?
2.思考
你怎样计算上述结果?有几种方法?
对于这一算式小丽和小明有两种算法:
因为 (-2)×7= -14
所以 (-14)÷7= -2
除法是乘法的逆运算 除以一个数等于乘这个数的倒数
请你比较他们的算法是否都正确?你能根据他们的算法总结出有理数除法的规律吗?
这个规律是:
【展示交流】
例1 计算
(1) 36÷(-9) (2) (-48)÷(-6)
(3) (-32)÷4×(-8) (4) 17×(-6)÷(-5)
体会:
对于两个整数的除法可采用直接除的办法,先确定 的符号,再把 相除.
例2
(1) (2)
体会:如果除数是分数,常常利用除以一个数等于 倒数,把除法转化为乘法,如果有理数乘除混合运算,往往先把除法转化为乘法,然后按照乘法法则确定积的符号,最后求出结果.
【盘点收获】
1.有理数除法则(1):除以一个不等于0的数,等于乘以这个数的倒数.字母表示为a÷b=a×
2.有理数除法法则(2):两数相除,同号得正、异号得负、并把绝对值相除.0除以任何一个不等于0的数,都得0
【自我检测】
1.若,则的值不可能为 ( )
A.0 B.1 C.2 D.-2
2.-的倒数是 ,两个非零有理数的和为0,则它们的商为 .
3.若则 0;若则 0.
4.两个有理数和除以这两个有理数的积,其商等于0,则这两个有理数( )
A.互为倒数 B.有一个数是0
C.互为相反数 D.互为相反数,且都不为零.
5.计算:
⑴ (2)
(3) (4)-8 ÷ (一)÷ (一)
(5)
运河初级中学“学讲计划”导学案
2.7有理数的乘方 (1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数乘方的实际含义并能进行有理数乘方的运算
【自主感知】
1.算一算
手工拉面是我国的传统面食.制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣,如此反复操作,连续扣六七次后便成了许多细细的面条.假如一拉扣了6次,你能算出一共有多少根面条吗
2.做一做
(1)将一张纸对折再对折(纸不得撕裂),直到无法对折为止.猜猜看,这时纸有几层
(2)对折1次纸变成2层,对折2次纸变成4层,依此类推,每对折1次层数就增加1倍.你折了多少次 请用算式表示你对折出来的纸层数.
【展示交流】
例1 计算:(1) 26 (2)62
(3)(-3)4 (4)-34
(5)(-4)3 (6)-43
想一想:(1)与(2)结果一样吗?(3)与(4)结果一样吗?(5)与(6)结果一样吗?为什么?
例2 (1) (2) (3) (4)
想一想:1.(2)与(4)它们相同吗?为什么?
例3(1) (2) (3) (4)
议一议:观察一下幂的符号,看看有何规律性的东西呢?
练一练
(1)________________的平方等于9; -14+1=_____
(2)(-4)2底数是______指数是______(-4)2=_______
(3) 34表示___个___ 相乘; (-2)3=______ ; 12003 -(- 1)2002=_______
(4) 一个数的平方为它本身,这个数是 ;
一个数的立方为它本身,这个数是
【盘点收获】
正数的任何次幂都是 ;负数的 幂是负数, 幂是正数;零的 幂都是零.任何一个数的偶次幂都是 数
【自我检测】
1.对于式子(-4)3,正确的说法是 ( )
A.-4是底数,3是冪 B.4是底数,3是冪
C. .4是底数,3是指数 D. -4是底数,3是指数
2.118表示 ( )
A.11个8相乘 B.11乘以8 C.8个11相乘 D.8个11相加
3.一个数的平方一定是 ( )
A.正数 B.负数 C.非正数 D.非负数
4.计算(-1)2002+(-1)2003的值等于 ( )
A.0 B.1 C.-1 D.2
5.如果一个有理数的偶次幂是非负数,那么这个数是( )
A.正数 B.负数 C.非负数 D.任何有理数
6. = ,—= ,= ,—= 。
7.平方等于64的数是 ,立方等于64的数是 。
8.计算
(1) (-6)2 (2) (3)
(4) (5) (6)
(7) (8)
运河初级中学“学讲计划”导学案
2.7 有理数的乘方 (2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
会用科学记数法表示比较大的数
【自主感知】
1.回顾
(1)什么叫乘方?什么叫幂;指出an中的指数、底数、幂
(2)计算32+42= ___________;(2)______________;
-32+(-3)2+(-0.5)3=_____________.
(3)“练一练”
10=10( )
100=10×10( )
1 000 =10×10×10=10( )
10 000=10×10×10×10=10( )
________ =________ =105
2.问题
光的速度大约是300 000 000米/秒;地球半径约为6400000米;赤道长约为40000000米;地球表面积约为:510000000000000平方米。
(1)上面各资料都有出现较大的数,这些数在记录的过程中非常容易出错,你能想办法使得我们记录得又快又准吗?
3.感知
一般地,一个大于10的数可以表示成a×10n 的形式,其中1≤a<10, n是正整数,这种记数方法叫做科学记数法
注意:把一个大于10的数可以写成a×10n时,必须遵循
① ②
【展示交流】
例1 1972年3月发射的“先驱者10号”,是人类发往太阳系外的第一艘人造太空探测器.至2003年2月人们最后一次收到它发回的信号时,它已飞离地球12200000000km.用科学记数法表示这个距离.
例2 请用科学记数法表示696 000;1 000 000; 58 000
【盘点收获】
1.科学记数法:把一个大于10的数表示成a×10n的形式,其中a是数位只有一位的整数,即1≤a<10,n是正整数,这种记数方法叫科学记数法.
2.科学记数法a×10n中n的确定:n为整数部分的位数减1.
3.用科学计数法表示一个比较大的数时,有两点要注意:
① ②
【自我检测】
1.用科学记数法记出下列各数:
(1) 7 000 000; (2) 92 000; (3) 63 000 000; (4) 304 000;
(5) 8 700 000; (6) 500 900 000;(7)374.2 (8) 7000.5.
2.下列用科学记数法记出的数,写出原数.
(1)2×106= (2)9.6×105= (3)7.58×107= ;
(4)6.03×108= (5)5.002×107= (6)5.016×102=
3.我国西部地区面积约为640万平方千米,用科学记数法表示为( )
A.640×104平方千米 B.6.4×106平方千米
C.64×105平方千米 D.4×107平方千米
4. 2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为( )
A.3.1×106元 B.3.11×104元 C.3.1×104元 D.3.10×105元
5.用科学记数法记出下列各数:
(1)地球离太阳约有一亿五千万千米;
(2)地球上煤的储量估计为15万亿吨以上;
(3)月球的质量约是7 340 000 000 000 000万吨;
运河初级中学“学讲计划”导学案
2.8有理数的混合运算(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1. 知道有理数的混合运算顺序,正确熟练地进行有理数的混合运算;
2.学会在计算前认真审题,确定运算顺序,计算中按步骤审慎进行,最后要验算的好习惯.
【自主感知】
1.指出下列各题的运算顺序:
(1)6÷3×2;
本题含有 种运算,应先算 ,再算 ;
(2)6÷;
本题含有 种运算,还含有 ,应先算 ,再算 ;
比较(1)(2)的运算顺序,你能得到什么结论?
_____________________________________________________________________________
(3)17-8÷+4×;本题含有 种运算,应先算 ,
再算 ;
(4)32-50÷22×+1;本题含有 种运算,应先算 ,再算 ;
然后再算 。
【展示交流】
例1 (1)计算: 8-23÷×
(2) 计算: 9+5×-2÷4
(3)3×[2-]-300÷5;
例2
(1)2×[-+ eq \b(-)]-2÷4;
(2) eq \b(--)÷ eq \b(-)+2×;
(3)-2×- eq \b(+3)÷3+ eq \b(+22)÷3-2×
【盘点收获】
对于有理数的混合运算,正确的运算顺序是:先 ,再 ,最后 .如果有括号,先算 .对于同一级运算,应按 顺序依次运算
【自我检测】
1.⑴(2×3)2= ;⑵2×32= ;⑶2+32= ;⑷(2+3)2=
2. -42= ;(-4)2= ;-5-9+16=
3.若ab互为相反数,mn互为倒数,则2(a+b)+3mn=
4.计算8÷(-4)×2的结果是( )
A.-4 B.-1 C.-16 D.4
5.-22+(-2)2+(-2)3+23的结果是( )
A.-8 B.0 C.8 D.24
5.计算
(1)-1× eq \b(1-)÷1 (2)[12-4×]÷4
(3)2×3-4×+15 (4)-14-×[2―2]
(5)-8-3×3―4 (6)-3-[-5+ eq \b(1-0.2×)÷]
运河初级中学“学讲计划”导学案
2.8有理数的混合运算(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1. 熟练地进行有理数的加、减、乘、除、乘方及混合运算;
2.运用有关运算律简化有理数的运算.
【自主感知】
1.回顾
(1)1÷2-2×3 (2)-1-[1-]
2. 试用两种不同的方法计算,并回答问题
eq \b(--)÷ eq \b(-)+ eq \b(-)
解法一: 解法二:
你认为哪一种方法简便?为什么?从中能得到什么启示?
【展示交流】
例1 计算: eq \b(-)×3÷3× eq \b(-)
例2 eq \b(-)÷ eq \b(-)+2×
【盘点收获】
1.有理数的混合运算顺序是先算 ,再算 ,最后算 ,如果有括号,要先算括号里的.
2.在有理数混合运算中,加法、乘法的所有运算律都能用;选择适当的运算律可以使计算简便.
【自我检测】
1.计算= ;-5+28÷(-2)×(-14)=
(-2)2+〔18-(-3)×2〕÷4= .
2.下列计算正确的是( )
A.(-1)4×(-1)3 B.2×32=62=36 C. D.
3.计算-2×32―(―2×32)=( )
A.0 B.-54 C.-72 D.-18
4.计算:
⑴ ⑵
⑶ ⑷
第2次对折
第3次对折
第1次对折
PAGE
1
1.1生活 数学
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.通过生活中常见的数字、图形的观察,思考感受生活中处处有数学。
2.乐于接触社会环境中的数字、图形信息,知道数学是我们表达和交流的工具。
【自主感知】
1.看看你父母的身份证,你从中能获得哪些信息?
2.找找你乘车的车票,你从中又能获得哪些信息?
3.以上两个事例说明我们的生活和 是分不开的.这样的例子你还能举出哪些?
4. 想想我们的交通工具的车轮、奥林匹克的五环旗、2008北京申奥的标志,2008北京奥运会的会徽、上海世博会的会标等生活当中的物体形状
你会觉得我们的生活和 是分不开的,这样的例子你还能举出哪些?
【展示交流】
例1 某粮店出售的三种品牌的面粉袋上,分别标有质量为(25±0.1)kg,(25±0.2)kg,(25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差多少?
例2 2008年第二十九届奥林匹克运动会在北京举办,会徽“中国印、舞动的北京”由印形部分、“Bei jing 2008”字样和奥林匹克五环组成,奥林匹克五环象征五大洲的团结,体现“和平、友谊、进步”的奥林匹克宗旨。你能说出印形的意义吗?
【拓展延伸】
1.运河中学举行校园歌手大赛,7位评委给某选手的评分如下表。计分方法是:去掉一个最高分,去掉一个最低分,其余分数的平均分作为该选手的最后得分,则该选手的最后得分为( )
评委 1 2 3 4 5 6 7
得分 9.8 9.5 9.7 9.8 9.4 9.5 9.4
A.9.59 B.9.58 C.9.57 D.9.56
2.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆最多把平面分成1×2+2=4个部分,3个圆最多把平面分成2×3+2=8个部分,4个圆最多把平面分成3×4+2=14个部分,那么10个圆把平面分成多少个部分?
【盘点收获】
1.本节课我们探究的主要内容是:
2.给我们的主要感受是:
3.探究一些规律性的东西时,我们采用的是 的方法
4.你还有哪些独到的感悟或体会呢?
【自我检测】
1.猜谜语:
(1)数字虽小却在百万之上(打一数字)
(2)2、4、6、8、10(打一成语)
(3)从严判刑(打一数字名词)
三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
2.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的最多奖励有多少项?
3.小华每天起床后要做的事情有穿衣(4分钟)、整理床(3分钟)、洗脸梳头(5分钟)、上厕所(5分钟)、烧饭(20分钟)、吃早饭(12分钟),完成这些工作共需49分钟,你认为最合理的安排应是多少分钟?
4.某风景区对5个旅游景点的门票价格进行了调整,据统计,调价前后各景点的游客人数基本不变。有关数据如下表所示:
(1)该风景区认为:调整前后这5个景点门票的平均收费不变,因此平均日总收入持平。问风景区是怎样计算的?
(2)游客认为:调整前后风景区的平均日总收入相对于调价前增加了9.4%,问游客是怎样计算的?
(3)你认为风景区和游客的说法,哪一种较能反映整体实际?
景点 A B C D E
原价(元) 10 10 15 20 25
现价(元) 5 5 15 25 30
平均日游客(千人) 1 1 2 3 2
运河初级中学“学讲计划”导学案
1.2活动 思考
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.在观察、实验、操作、猜想和归纳等数学活动中学会思考
2.能收集、选择、处理数字信息,作出合理的推断或大胆的猜想
【自主感知】
活动一:用一张长方形纸片按如图的方法折叠、裁剪、展开,你会得到什么图形?
理由是:
活动二:按下图方式,用火柴棒搭三角形
搭1个三角形需要火柴棒 根; 搭2个三角形需要火柴棒 根;
搭3个三角形需要火柴棒 根; 搭10个三角形需要火柴棒 根;
搭100个三角形需要火柴棒 根;
问:搭建三角形的个数与需要火柴棒的根数之间有什么的关系?说说期中的规律
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
【展示交流】
例1 观察下列已有式子的特点,在 内填入恰当的数:
1+2+1=
1+2+3+2+1=
1+2+3+4+3+2+1=
1+2+3+4+5+4+3+2+1=
1+2+3+…+2006+2007+2008+2007+2006+…+3+2+1=
例2 将一些数排列成下表:
第1列 第2列 第3列 第4列
第1行 1 4 5 10
第2行 4 8 10 12
第3行 9 12 15 14
试探索:(1)第10行第2列的数是多少?
(2)81所在的行和列分别是多少?
(3)100所在的行和列分别是多少?
【盘点收获】
1.本节课主要内容是探究数式、图形、表格所体现的
2.主要的探求方法是:
3.在数学实践中,规律的探求需要我们去大胆的
4.你还有哪些独到的见解和感悟呢?请写一写
【自我检测】
1.在 上填上适当的数:
(1)2,4,6, ,10,… (2)1,12,123,1234, ,123456,…
(3)1,3,6, ,15,21,… (4)1,1,2,3,5, ,13,21,…
2.日历表中某月所有星期六的日期数全加起来等于85,这个月的第一天是( )
A.星期三 B.星期四 C.星期五 D.星期六
3.将一张长方形的纸对折,如图,可得到一条折痕(图中虚线),连续对折,对折时每次折痕与上次折痕保持平行,连续对折三次后,可以得到7条折痕;那么连续对折四次后,可以得到 条折痕;连续对折五次后,可以得到 条折痕.
4.把一个长为9、宽为4的长方形分成两块,然后拼成一个正方形.(说说你的做法)
运河初级中学“学讲计划”导学案
2.1 正数与负数
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道正负数的概念,
2.会区分正负数
3.能用正负数表示具有相反意义的量.
【自主感知】
1.我们知道珠穆朗玛峰海拔8844米,那么吐鲁番盆地的最低处海拔高度比海平面低155米该如何表示呢?
②结合课本四幅图片,说出图中所给数字所代表的含义.
2.填一填
正负数概念:____________________________________________________,
正负数表示方法:________________________________________________;
0既不是__________________________,也不是________________________.
3.生活中常会遇到一些具有相反意义的量:如增加与 ,收入与 等,对于这些具有相反意义的量,若规定其中一个量为正,则另一个就为负.
【展示交流】
例1 指出下列各数中,哪些是正数?哪些是负数?
练一练 请把下列各数填入相应的集合中:
例2 填空
(1)如果向北行走8km记作+8km,那么向南行走5km记作 ;
那么向南行走-4km记作 ,向北行走-7km记作
(2)如果运进粮食3t记作+3t,则-4t表示 ;
(3)如果节约了-20千瓦,实际上是 ;
(4)如果负一场得-1分,实际上是 .
练一练:
(1)如果买入大米200kg记作+200kg,则卖出120kg大米记作
(2)如果-50元表示支出50元,那么+40元表示 ;
(3)太平洋最深处的马里亚纳海沟低于海平面11034m,它的海拔高度可以表示为 ;
【拓展延伸】
1.下表列出了几个城市与北京的时差(正数表示同一时刻比北京早的时数),如果现在是北京时间8:30.
城市 东京 纽约 巴黎 芝加哥
时差 +1 -13 -7 -14
⑴东京时间是多少 纽约、芝加哥的时间是多少
⑵小刚现在给远在巴黎的叔叔打电话,你认为合适吗
【盘点收获】
1.正数实质上是指 的数;
负数实质上是指 的数
2.一个数的前面带有正号一定是正数吗?一个数的前面带有负号一定是负数吗?
你的理由是
3.具有相反意义的量必须满足的条件是
①
②
【自我检测】
1.任举4个正数: ;任举4个负数: .
2.把下列各数填入相应的集合中:
正数集合:{ ,…}
负数集合:{ ,…}
3.如果时针顺时针方向旋转900记作-900,那么逆时针方向旋转600记作 ;
4.如果将低于警戒线水位0.27m记作-0.27m,
那么+0.42m表示 ____
5.用正,负数表示下列问题中的量:
①某商场在“五一”期间购进空调390台,销售了295台;
②某日A股上涨1个百分点,B股下跌3个百分点.
6.中午12时,水位低于标准水位0.5米记作-0.5米,下午1时水位上涨了1米,下午5 时水位又上涨了0.5米,则
①下午1时的水位可记录为 ,下午5时的水位可记录为 .
②下午5时的水位比中午12时的水位高 米.
运河初级中学“学讲计划”导学案
2.2有理数与无理数
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道什么是整数和分数
2.能分清有理数与整数和分数之间的关系,能对有理数进行正确分类
3.知道什么是无理数,并能对一个数的归属做出正确判断.
【自主感知】
1.学校的图书馆馆藏书近20万册,可是图书管理员阿姨总能很快地将你要借的书找出来,你知道这是为什么吗
2.我们小学学过哪些数?是怎样分类的?现在我们引入了负数,还能否按原来的标准分类?若能,分分看;还有其他的标准吗?试一试
3.整数包括
分数包括
4.有理数就是 的统称;
实质上就是 的数
于此相反无理数就是 的数
例如
【展示交流】
例1 把下列各数填在相应集合内:
正数集合:{ ,…}
负数集合:{ ,…}
整数集合:{ ,…}
分数集合:{ ,…}
例2 把下列各数填在相应的大括号内:
,0,π,314,-,,,-0.55,8,1.121 221 2221…(相邻两个1之间依次多一个2),0.2111,201,999.
正数集合:{ }
负数集合:{ }
有理数集合:{ }
无理数集合:{ }
【拓展延伸】
1.下列说法中,正确的是( )
A.有理数都是有限小数 B.无限小数都是无理数
C.3.14是无理数 D.π是无理数
2.①正整数和负整数统称为整数.②-0.5既是分数,也是负数.③0只表示没有.④正数和负数统称为有理数.⑤一个数不是正数就是负数.⑥既不是正数也不是整数的有理数是负分数.以上的说法中正确的有
3.下列四项中,错误的是( )
A.存在最小的自然数 B.存在最小的正有理数
C.不存在最大的正有理数 D.不存在最大的负有理数
4.写出所有适合下列条件的数:
(1)不大于3的正整数: ;
(2)大于-5的负整数: ;
(3)大于-3且不大于4的整数: .
【盘点收获】
1.有理数有两个分类标准,分别是
有理数 有理数
2.有理数就是 的数;无理数就是 的数
3. 是数学中一个最重要的数学思想,因为这是我们正确认识事物的关键.
【自我检测】
1.判断正误:
(1)不循环小数是无理数( )
(2)一个有理数不是正数就是负数( )
(3)有理数不一定是有限小数( )
(4)分数中有有理数,也有无理数,如就是无理数( )
2.一m是一个有理数,则它一定是( )
A.负数 B.正数 C.负数或负数 D.负数、零或正数
3.下列说法正确的是( )
A.整数就是正整数和负整数 B.分数包括正分数和负分数
C.正数和负数统称为有理数 D.3.1415926不是有理数
4.关于0的说法正确的是( )
A.不是正数也不是负数 B.是正数 C.是负数 D是正整数
5.既不是正数也不是整数的有理数是( )
A.0和负分数 B.负分数 C.负整数和负分数 D.正整数和正分数
6.不小于-2.5而小于2.8的非负整数有( )
A.2个 B.3个 C.4个 D.5个
运河初级中学“学讲计划”导学案
2.3数轴(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.了解数轴的概念,知道数轴的三要素,会画数轴,
2.能将已知数用数轴上的点表示出来,能说出数轴上已知点表示的数.
【自主感知】
1.感知
温度计可以用来测量室内温度,你能读出它们的示数吗?你能在温度计上找出表示-5°C,-15°C的刻度吗?
2.像__________________________________________________的直线叫做数轴.
数轴的三要素:_____________ 、 _____________ 、_____________
【展示交流】
例1 判断下列数轴的画法是否正确,若不正确,请在右边指出错误原因
例2 如图,指出数轴上点A、B、C表示的数
例3 在数轴上画出表示下列各数的点
2,-1.5,0,-,1.5,-
【拓展延伸】
数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.请利用数轴回答下列问题:
⑴ 在数轴上,到原点的距离为5的点有_______个,它们表示的数是______________;
⑵ 在数轴上,从表示2的点出发,先向右移动3个单位长度,再向左移动6个单位长度,最后的终点表示的数是_____________________
⑶ 在数轴上,点M表示数2,那么与点M相距4个单位的点表示的数是_____________
【盘点收获】
1.数轴就是具有 、 、 的一条直线.
2. 可以用数轴上的点来表示 ,表示正数的点都在原点的_________侧,表示负数的点都在原点的_________侧.
3. 也是数学中一个重要的数学思想,它可以起到“以形助数,以数助形”的作用.
【自我检测】
1.下列说法错误的是( )
A.规定了原点、正方向和长度的直线叫数轴
B.所有的有理数都可以用数轴上的点表示
C.数轴上的原点表示数0
D.数轴上表示一3.33的点在表示一3的点的左边
2.在数轴上,到原点距离5个单位长度,且在数轴右边的数是( )
A.-5 B.+5 C. D.15
3.数轴上离开原点个单位长度的点所表示的数是__________.
4.指出数轴上A、B、C、D、E表示的数.
5.小明家,学校,书店在同一笔直的东西走向大街上,一天小明从学校(记作O点)出发,向西走50m回家拿钱(记作A点),又从家向东走110m到书店(记作B点)买书,当他从书店向西走80m时(记作C点)遇到小伟.
⑴以学校(O点)为原点,向东为正方向建立数轴,并在数轴上表出A,B,C,O的位置.
⑵C点位于学校的哪个方向,离学校的距离是多少?
6.在数轴上的点A表示-3,现在把点A先向右移动7个单位,再向左移动4个单位,则到达终点所表示的数是什么?
7.数轴上的点A和点B所表示的数分别是-1,3,若要使点A表示的数是点B表示的数的2倍,保持B点不动,应将点A怎样移动?
运河初级中学“学讲计划”导学案
2.3数轴(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.进一步体会数轴上的点与有理数的对应关系,体会“数形结合”的思想方法。
2.能利用数轴比较有理数的大小,
【自主感知】
某日,北京,长春,江苏,黑龙江的最高气温分别是0°C,-2°C,5°C,-3°C
1 你能直观地知道哪个温度高哪个温度低吗?对温度计来说,越是向上温度越大还是越小?
② 在数轴上画出表示这些温度的点,你能得到什么结论?
结论:_____________________________________________________________________
___________________________________________________________________________
【展示交流】
例1 比较下列各组数的大小
⑴ 5和0 ⑵ -和0 ⑶ 2和-3 ⑷ -3,1.5和0
例2 比较下列各组数的大小
⑴ -3.5和-0.5 ⑵ -和-0.25
变式:比较下列各组数的大小
1 -1 -4 0 5 -2 -
步骤:
⑴
⑵
⑶
例3 在数轴上表示-2和1,并根据数轴指出大于-2而小于1的整数。
【拓展延伸】
1. 观察数轴,能否找出符合下列要求的数:
(1)最大的正整数和最小的正整数; (2)最大的负整数和最小的负整数;
(3)最大的整数和最小的整数; (4)最小的正分数和最大的负分数.
(5)最小的有理数和最大的有理数
2.在数轴上有三个点A、B、C分别表示一3、0、2,按要求回答
(1)将A向右移动6个单位后,三个点表示的数谁最大,是多少
(2)将C向左移动4个单位后,此时B点表示的数比C点的数大多少
(3)怎样移动A,B,C中的两个点,才能使这三个点表示的数相同 有几种方法
【盘点收获】
1.在数轴上的两个点中,右边的点表示的数 左边的点表示的数;正数 0;
小于0;正数大于 .利用这个性质可以比较两个有理数的大小.
2.数轴上点的平移所对应的数:
点向右平移几个单位,那么对应的数就在原来的基础上 (填“加上”或“减去)几;
向左平移几个单位,那么对应的数就在原来的基础上 (填“加上”或“减去”)几.
【自我检测】
1.填空
(1)不小于-3的负整数有哪些?
(2)比-2小4的数是什么数?
(3)-3比-9大多少?
(4)比-3小5的数是 ;比-3大5的数是
(5)-2和6的正中间的数是什么?
2.从数轴上观察,不小于-3而且不超过4的正整数有( )
A.5个 B.6个 C.7个 D.8个
3.下列说法正确的是( )
A、0是最小的有理数
B、若有理数m>n,则数轴上表示m的点一定在表示n的点的左边
C、一个有理数在数轴上表示的点离原点越远,这个有理数就越大
D、既没有最小的正数,也没有最大的负数。
4.点M从数轴上原点开始,先向左移动5个单位长度,再向右移动2个单位长度,此时点A所表示的数是
5.将有理数一4,5、3、0、一1、1、一3数轴上表示出来,并用“<”把这些数从小到大的顺序连接起来.
【探究与思考】(这三个小题仅供同学们课下研究)
1.一跳蚤在一直线上从O点开始,第1次向右跳1个单位,紧接着第2次向左跳2各单位,第3次向右跳3个单位,第4次向左跳4个单位……依此规律跳下去,当它跳第100次落下时,落点处离O点的距离是__________个单位。
2.1路公交车在笔直的淮海路上来回奔跑,起点站是A,由A向东走5站是终点站B,回头向西走3个站,这时公共汽车在A站的何位置 若由A→B→A算走一趟,每站间路程是S千米,每千米耗油m升,则该公共汽车1天10趟耗油多少升
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道什么是有理数的绝对值以及表示方法,
2.能求一个有理数的绝对值并进行有关的简单计算,
3.会比较两个负数的大小.?
【自主感知】
1.一天,汽车司机张师傅从车站出发,沿东西方向行驶,规定向东为正,若向东行驶3千米,记作_____ ;若向西行驶2千米,记作_____ .若每千米耗油10升,则向东行3千米,耗油量是 ______ ,向西行2千米,耗油量是 ______ .
2.假设把汽车行的路想像成数轴,将车站定为原点,向东行驶3千米到达A点,向西行驶2千米到达B点.数轴上点A与原点的距离是____个单位长度,点B与原点的距离是_____个单位长度.
定义: 叫做这个数的绝对值.绝对值的符号:“ ”
注意:1.任何有理数的绝对值都是 数
2.绝对值最小的数是 ; (填“有”或“无”)绝对值最大的数
【展示交流】
例1 在数轴上画出表示下列各数的点:,并写出它们的绝对值.
例2 求下列各组数的绝对值,并分别比较它们绝对值的大小:
(1)-3.5与4 (2)-3与-6
思考:对第(2)题的解答你发现比较两个负数的大小有怎样的规律呢?
规律:
【拓展延伸】
1.某厂生产闹钟,检验时,比标准时间多的记为正数,比标准时间少的记为负数,请根据下表,选出最准确的闹钟.
1 2 3 4 5
+2s -3.5s 6s +7s -4s
误差不超过5秒的为合格品,否则为次品,问有几台合格?
2.,计算的值
【盘点收获】
1.数的绝对值实质上是 的距离,所以一个数
的绝对值不能是负数,也就是说一个数的绝对值一定是 数.
2.两个负数比较,绝对值 的反而小.
【自我检测】
1.计算
|-3|= , ||= ,
|-0.4|= , |0|= __
|9|= __ , |-2|=
2.用“<”把|-3|、|-0.4|及|-2|连接起来.
3.填空:
(1)绝对值小于3的所有整数是________________,非正整数是 ____
(2)若|x|=6,则x =
(3)在数轴上A表示-,点B表示,则点 离原点的距离近些.
4.计算:
(1)|—3|×|—6.2| (2)|—5| + |—2.49|
(3)|—|—|| (4) |—|÷||
5.某车间生产一批圆形零件,从中抽取8件进行检验,比规定直径长的毫米数记为正数,比规定直径短的毫米数记为负数,检查记录如下:
1 2 3 4 5 6 7 8
+0.3 -0.2 -0.3 +0.4 0 -0.1 -0.5 +0.3
指出第几个零件最标准?最接近标准的是哪个零件?误差最大的是哪个零件?
6.(1),求的值.
(2)已知| a+2 | + (b-3)2 =0,求a+b的值.
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数的相反数概念及表示方法,
2.会求一个有理数的相反数以及有关的简单计算
【自主感知】
1.数轴上到原点的距离是3的点有几个 它们到原点的距离各是多少 它们之间还有什么关系
2.在数轴上到原点的距离是2.5的点有几个 它们到原点的距离各是多少 它们之间还有什么关系
3.观察下列各对有理数,你发现了什么?
5与-5 -2.5与2.5
定义:像5与-5 、-2.5与2.5 …这样 、 的两个数,叫做互为相反数,其中一个是另一个的________ (只有符号不同的两个数).
规定:零的相反数是零
注意:①正数的相反数是________;负数的相反数是________;0的相反数是_________.
②表示一个数的相反数,只要在这个数的前面添加一个“ ”号即可.
【展示交流】
例1 求出3、-4.5、0、的相反数(在一个数的前面添一个“-”,就表示这个数的相反数)
例2 化简:.
思考:对上题的解答可以看出,对于双重符号的化简问题有个规律,这个规律是
例3 求6、-6、0、 、 的绝对值,有什么发现
归纳:相反数的性质:
①__________________________________________
②__________________________________________
③__________________________________________
思考:一个数的绝对值与这个数本身或它的相反数有什么关系?
一个正数的绝对值是____ 一个负数的绝对值是______
0的绝对值是______
【拓展延伸】
(1) 绝对值不小于3的整数是什么?绝对值小于5的整数是什么?绝对值小于3的整数是否都小于绝对值小于5的整数?
(2)已知x是整数,且2.5<|x|<7,求x.
(3)已知点A,B分别为数轴上表示互为相反数的两个点,且A,B两点间的距离为5,其中A在B的左边,请你写出这两个点所表示的数.
【盘点收获】
1.本节课的知识点你认为有哪些?列举出来
【自我检测】
1.下列各组中互为相反数的是( )
A.一2与 B,|-2|与2 C.一2.5与|-2| D.-0.5与|-|
2.下列各数中互为相反数的是 ( )
A、与0.2 B、与-0.33 C、-2.25与 D、5与-(-5)
3.下列各对数中互为相反数的是 ( )
A.-(+3)和+(-3) B.-(-3)和+(-3) C.-(+3)和-3 D.+(-3)和-3
4.在-中,负数有( )
A.1个 B.2个 C.3个 D.4个
5.下列说法:① 如果a=-13,那么-a=13, ② 如果a=-1,那么-a=-1, ③ 如果a是非负数,那么-a是正数, ④如果a是负数,那么+1是正数, 其中正确的是 ( )
A ①③ B ①② C ②③ D ①④
5. 若,则是( )
A.0 B.正数 C.负数 D.负数或0
运河初级中学“学讲计划”导学案
2.4绝对值与相反数(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会比较两个有理数的大小,
2.进一步感受数形结合等数学思想方法.
【自主感知】
一、回顾
1.什么叫绝对值?如何求一个数的绝对值?
2.什么叫相反数?互为相反数的两个数有什么性质?
4、填空:
(1)+|-2|=________ (2)-|+4|=________
(3)|+3.5|-|-2|=________ (4)-(-2.3)=_____
(5) +(-5)=________ (6)-|-4|=________
二、探究
1.两个有理数如何比较大小 数轴上两数如何比较?
结论
2.绝对值大的那个数数就一定大吗
思考:
(1)正数的绝对值大于0的绝对值,正数比0大吗?
(2)负数的绝对值大于0的绝对值,负数比0大吗?
(3)正数的绝对值就是它本身,绝对值大的正数大,绝对值小的正数小吗?
(4)负数的绝对值是它的相反数,绝对值大的负数大,绝对值小的负数小吗?
3、两个有理数的大小与这两个数的绝对值的大小有什么关系?
结论:
【展示交流】
例1 (1)比较-9.5与- 1.75的大小
(2)比较-与-(-2.9)的大小
例2 数a、b在数轴上的位置如图所示,则下列判断中,正确的是( )
A.a>-1 B.b>1 C.a<-1 D.b<0
例3 有理数、、在数轴上的位置如图,
判断正负,用“>”或“<”填空
-_0, - _0, +_0
【盘点收获】
1.两个有理数比较时,重点是同号比较,通正比较, 的大;同负比较, 的反而小.
2.两个数相减,大的减小的差 0;小的减大的差 0(填“大于”或“小于”)
【自我检测】
1.三个数-3、-4、0依次从小到大排列的顺序是 ( )
A.0<-4<-3 B.-3<-4<0
C.0<-4<-3 D.-4<-3<0
2.下面四个结论中,正确的是 ( )
A.= B.-2>0
C.-2< D. >0
3.比较大小:
(1)3 -7 (2)-5.3 -5.4
(3)- - (4)-|-0.4| -(-0. 4)
4.化简:
(1)-= (2)=
(3)= (4)=
5.飞机上升3000米,记作+3000米;又下降3000米,记作-3000米,那么飞机还是原来的高度
小明数学竞赛获奖,爸爸奖励50元,记作+50元;他很高兴,去书店买书,花了50元,记作-50元,那么他的剩余钱恰好为0
(1)+3000和-3000,+50和-50有什么关系?
(2)猜想两个数互为相反数,那么它们的和是多少?
(3)用你第(2)步的结论计算:字母a、b、c、d表示有理数,且a、b互为相反数,正数c的绝对值是2,d的相反数是-5,求a+b+c×d的值
运河初级中学“学讲计划”导学案
2.5 有理数的加法与减法(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.探索有理数加法法则,理解有理数的加法法则
2.能熟练进行有理数的加法运算
3.有初步的分类思想
【自主感知】
1.填一填
足球队甲、乙两队比赛,主场甲队4:1胜乙队,赢了3球,客场甲队1:3负乙队,输了2球,甲队两场比赛累计净胜球1个,你能把这个结果用算式表示出来吗?
你知道的比赛中胜负难料,两场比赛的结果还可能哪些情况呢?动动手填表:
赢球数 净胜球 算式
主场 客场
3 ‐2
‐3 2
3 2
‐3 ‐2
3 0
0 ‐3
你还能举出一些应用有理数加法的实际例子吗?
例如:第一天水位下降了5厘米,第二天水位上涨了8厘米,两天水位变化情况是上涨了3厘米.用算式表示这个结果。
算式:_______________________
2.讨论:两个有理数相加时,和的符号及绝对值怎样确定?你能找到有理数相加的一般方法吗?
有理数加法法则:
同号两数相加,__________________________________________________.
异号两数相加,_______________________________________;
一个数与0相加,__________________.
【展示交流】
例1 计算下列各题:
(1)(-180)+(+20) 2)(-15)+(-3)
(3)5+(-5) (4)0+(-2)
例2
某仓库原有粮食80吨,第一天运进粮食54吨,第二天又运出粮食32吨,现在仓库共有粮食多少吨?
思考:两个有理数相加,和一定比两个加数大吗?
【盘点收获】
1.有理数的加法运算主要搞清两个方面的问题
① ;② .
【自我检测】
一、选择
1.一个正数与一个负数的和是
A.正数 B.负数
C.零 D.以上三种情况都有可能
2.绝对值不大于3的所有整数的和为
A. 6 B. -6 C.±6 D.0
3.两个有理数的和
A.一定大于其中的一个加数 B.一定小于其中的一个加数
C.大小由两个加数符号决定 D.大小由两个加数的符号及绝对值而决定
二、判断
1.绝对值相等的两个数的和为0 ( )
2.若两个有理数的和为负数,则这两个数至少有一个是负数( )
3.如果某数比-5大2,则这个数的绝对值是3 ( )
三、填空题:
1. ⑴ (+3)+(+7)=______ ⑵ (+3)+(—8)=_______
⑶ (—12)+(—5)=_________ ⑷ (—37)+22 =_________
⑸ 0+(—19) =___________ ⑹ (—7)+ |—5 |=_________
2. 若 | m |= 2, | n | =5 ,且m>n, 则m+n =___________
四、计算;
⑴(+10)+(—4) ⑵(—15)+(—32) ⑶(—9)+ 0
五、列式解答
(1)一个数与-5的差为-8,求这个数
(2)一个数与9的差为-5,求这个数
六、土星表面夜间的平均气温为-150℃,白天的平均气温比夜间高27℃,那么白天的平均气温是多少?
七、潜水员原来在水下15米处,后来上浮了8米,又下潜了20米,这时他在什么位置?要求用加法解答。
运河初级中学“学讲计划”导学案
2.5 有理数的加法与减法(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.经历探索有理数加法运算律的过程,理解有理数的加法运算律的实质;
2.能运用加法运算率简化加法运算;
【自主感知】
一、算一算
情景1: 情景2:
3+(-5)=
(-5)+ 3 =
二、总结
上面两个情景中所使用的数学运算律是:
1.加法的交换律:
2.加法的结合律:
【展示交流】
例1 计算:
1.(-23)+(+58)+(-17) 2.(-2.8)+(-3.6)+(-1.5)+3.6
3.
思考:有理数的加法运算中,利用运算律,我们往往采取如下的策略
①
②
③
④
练习:计算:
1. (-11)+8+(-14) 2. (-4)+(-3)+(-4)+3
3. 4. 8+(-2)+(-4)+1+(-3)
5. 0.35+(-0.6)+0.25+(-5.4) 6.
【盘点收获】
谈谈在加法的运算中灵活性有哪些方面
【自我检测】
1.计算:
(1)(-3)+40+(-32)+(-8) (2)43+(-77)+27+(-43)
(3)18+(-16)+(-23)+16 (4)(-3)+(+7)+4+3+(-5)+(-4)
(5)5.6+(-0.9)+4.4+(-8.1) (6)
2.计算
1+(-2)+(-3)+4+5+(-6)+(-7)+8+……+2001+(-2002)+(-2003)+2004
3.求绝对值大于3且小于6的所有整数的和。
4.某出租车沿公路左右行驶,向左为正,向右为负,某天从A地出发后到收工回家所走的路线如下:(单位:千米)
⑴ 问收工时离出发点A多少千米?
⑵ 若该出租车每千米耗油0.3升,问从A地出发到收工共耗油多少升?
运河初级中学“学讲计划”导学案
2.5有理数的加法与减法(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.探索有理数减法法则的过程;
2.能熟练地进行有理数的减法运算;
3.体会转化的思想方法
【自主感知】
1.问题
一天的最高气温与最低气温的差叫做日温差。
如果某天的最高气温是5℃,最低气温是3℃,那么这天的日温差是多少(列式计算)
如果某天的最高气温是5℃,最低气温是-3℃,那么这天的日温差是多少(列式)
2.感知
猜想:有理数的减法法则:减去一个数等于
即表示成a-b=a+(-b).
验证:
(1)如果某天A地气温是3℃,B地气温是-5℃,A地比B地气温高多少?
3-(-5)=3+ ;
(2)如果某天A地气温是-3℃,B地气温是-5℃,A地比B地气温高多少?
(-3)-(-5)=(-3)+ ;
(2)如果某天A地气温是-3℃,B地气温是5℃,A地比B地气温高多少?
(-3)-5=(-3)+ ;
【展示交流】
例1 计算:
①15-(-7) ②(-8.5)-(-1.5)
③ 0-(-22) ④(+2)-(+8)
⑤(-4)-16 ⑥
练一练:口答
(1) 3 – 5 (2) 3 – (-5)
(3)(-3)– 5 (4)(-3) –(-5)
(5)–6 -(-6) (6)-7-0
(7)0 -(-7) (8)(-6)-6
(9)9 -(-11) (10) 6-(-6)
思考:在有理数范围内,差一定比被减数小吗
例2.求出数轴上两点之间的距离:
(1)表示数10的点与表示数4的点;
(2)表示数2的点与表示数-4的点;
(3)表示数-1的点与表示数-6的点。
思考:通过对例2的求解可以得出这样一个结论
求数轴上任意两点的距离只要求出两个点所对应的数的 的绝对值即可.
【拓展延伸】
(1)-13.75比少多少?
(2)从-1中减去-与-的和,差是多少?
【盘点收获】
1.有理数的减法法则:________________________________________
(其实质是将减法转化为___________)
2.数轴上两个点之间的距离就是这两个点表示的数的差的 .
【自我检测】
1.下列说法中正确的是( )
A.减去一个数,等于加上这个数.
B.零减去一个数,仍得这个数.
C.两个相反数相减是零.
D.在有理数减法中,被减数不一定比减数或差大.
2.下列计算中正确的是( )
A.(—3)-(—3)= —6 B . 0-(—5)=5
C.(—10)-(+7)= —3 D . | 6-4 |= —(6-4)
3.下列说法中正确的是( )
A.两数之差一定小于被减数.
B.减去一个负数,差一定大于被减数.
C.减去一个正数,差不一定小于被减数.
D.零减去任何数,差都是负数.
4.若不为0的两个数的差是正数,则一定是( )
A.被减数与减数均为正数,且被减数大于减数.
B.被减数与减数均为负数,且减数的绝对值大.
C.被减数为正数,减数为负数.
D.以上3种均可满足条件.
5.(1)(—2)+________=5; (—5)-________=2.
(2)0-4-(—5)-(—6)=___________.
(3)月球表面的温度中午是1010C,半夜是-153oC,则中午的温度比半夜高____.
(4)已知一个数加—3.6和为—0.36,则这个数为_____________.
(5)已知b < 0,则a,a-b,a+b从大到小排列________________.
运河初级中学“学讲计划”导学案
2.5有理数的加法与减法(4)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会进行有理数的加减混合运算
2.会计算省略加号和括号的有理数加减混合运算
【自主感知】
1.回顾
计算:
(1)7-(-4)+(-5) (2)-2-12+(-3)+8-(-6)
根据有理数的减法法则,有理数的加减混合运算可以统一为___________
2.新知
在把有理数加减混合运算统一为加法的算式中,负数前面的加号可以省略不写.
例如7+4+(-5)可以写成7+4-5,它表示7、4与(-5)的和.
计算:
(-4)+9-(-7)-13
解:原式=-4+9+(+7)+(-13) 减法转化为加法
=-4+9+7-13 省略加号的和
=-4-13+9+7 加法交换律
=-17+16 同号两数相加
=-1 异号两数相加
11-39.5+10-2.5-4+19
解:原式=11+10+19-39.5-2.5-4 加法交换律
=【(11+19)+10】+【(-39.5-2.5)-4】 加法结合律
=40-46 同号两数相加
=-6 异号两数相加
【展示交流】
例1 计算
(1)-3-5+4 (2)-26+43-24+13-46
练一练:计算
(1)7-(-6)-(-5) (2)-21-12+33+12-67
(3)5.4-2.3+1.5-4.2 (4)
例2 巡道员沿东西方向的铁路进行巡视维护。他从住地出发,先向东行走了7km,休息之后继续向东行走了3km;然后折返向西行走了11.5km.此时他在住地的什么方向?与住地的距离是多少?
【盘点收获】
1.有理数加减混合运算统一为有理数的_________运算
2.性质符号与运算符号的辨析
3.谈谈你对本节课的见解
【自我检测】
1.判断题
(1)运用加法交换律,得-7+3=-3+7. ( )
(2)-5-4=-9.( ) -5-4=-1.( )
(3)两个数相加,和一定大于任一个加数. ( )
(4)两数差一定小于被减数. ( )
(5)零减去一个数,仍得这个数. ( )
2.选择题
(1)把(+5)-(+3)-(-1)+(-5)写成省略括号的和的形式是 ( )
A.-5-3+1-5 B.5-3-1-5
C.5+3+1-5 D.5-3+1-5
(2)算式8-7+3-6正确的读法是 ( )
A.8、7、3、6的和 B.正8、负7、正3、负6的和
C.8减7加正3、减负6 D.8减7加3减6的和
(3)两个数相加,其和小于每个加数,那么这两个数( )
A.同为负数 B.异号 C.同为正数 D.零或负数
(4)甲数减去乙数的差与甲数比较,必为( )
A.差一定小于甲数 B.差不能大于甲数
C.差一定大于甲数 D.差的大小取决于乙是什么样的数
3.把下列各式写成省略括号的和的形式
(1)(-28)-(+12)-(-3)-(+6)
(2)(-25)+(-7)-(-15)-(-6)+(-11)-(-2)
4.计算下列各题
(1)(+17)-(-32)-(+23) (2)(+6)-(+12)+(+8.3)-(+7.4)
5.小虫从某点A出发,在一直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:厘米):+5,—3,+10,—8,—6,+12,—10.(1)小虫最后是否回到出发点A?
(2)小虫距离出发点最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则小虫一共得到多少粒芝麻?
运河初级中学“学讲计划”导学案
2.6 有理数乘法与除法(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数乘法的运算法则
2.会进行有理数的乘运算
【自主感知】
1.回答课本提出的问题
① ; ②
③ ; ④ .
2.如果我们把水位上升为正,下降为负;几天后记为正,几天前记为负,那么上面的四个问题你能否用有理数运算的式子来表达,试一试
① ; ②
③ ; ④ .
3.解决课本中的“想一想”
4.填写课本中的相关表格
5.总结有理数乘法法则
_____________________________________________________________________________
___________________________________________________________________________.
【展示交流】
例题1 计算:
(1) (- 4)×5; (2) (- 5) ×(-7)
思考:正确进行有理数的乘法运算要注意两个关键点,这两个关键点分别是
① ②
例2 计算;(1)2×(一3) × 5×(一1) (2)(一)××(一)×(一)
思考:对于两个以上的有理数相乘,仍然要注意两个关键点,不过在确定积的符号时,只须看 的个数即可;负因数的个数为 ,积为负;负因数的个数为偶数时,积为 .
【盘点收获】
1.有理数乘法法则:两数相乘,同号得 ,异号得 ,并把绝对值相乘,任何数同零相乘都得 .
2.几个不是0的有理数相乘,积的符号由 的个数决定,当负因数有奇数个时、积为 ,当负因数有 个时积为正.
【拓展延伸】
1.若规定,则 , .
2.若“!”是一种运算符号,且1!=1,2!=2×1,3!=3×2×1,4!=4×3×2×1,……,
则
【自我检测】
1.(-4)×()的结果为 ( )
A.6 B.-6 C.2 D.-2
2.互为相反数的两数相乘,积为 ( )
A.正数 B.负数 C.0 D.负数或0
3.五个有理数相乘,积的符号为负,则负因数的个数有 ( )
A.1个 B.3个 C.5个 D.1个或3个或5个
4.计算:⑴ , ⑵ (+18) ×(-6)= ,
⑶ 0×()= , ⑷= .
5.计算下列各题:
(1) 3 ×(-5)×(-7)× 4 (2)15 ×(-17)×(-19)×0
(3) (4)
6.初一年级共100名学生,在一次数学测试中以90分为标准,超过的记为正,不足的记为负,成绩如下:
人数 10 20 5 14 12 18 10 4 9 6 2
成绩 -1 +3 -2 +1 +10 +2 0 -7 +7 -9 -12
请你算出这次考试的平均成绩。
运河初级中学“学讲计划”导学案
2.6有理数乘法与除法(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.熟记有理数的乘法法则
2.会运用乘法运算率简化乘法运算.
【自主感知】
1.算一算,看一看,想一想
第一组:
(1)3×4= ______ (2)4×3= ______
(3)(-3)×4= ______ (4)4×(-3)= ______
(5)3×(-4)= ______ (6)(-4)×3= ______
(7)(-3)×(-4)= _____ (8)(-4)×(-3)= ______
第二组:
(1)[(-3)×4]×0.5=_______ (-3)×(4×0.5)=_______
(2)[3×(-8)]×0.125=________ 3×[(-8)×0.125]=_______
第三组:
(1) _______ _______
(2)(-4)×(-3)+(-4)×5=______ (-4)×(-3+5)=_________
通过你的计算能得到什么结论?
2.计算
(1) ;(2) ;(3) .
像这样乘积为 的两个数,我们称为互为倒数,其中一个是另一个的倒数.
【展示交流】
例1 (1) (2)
思考:通过上两个题的计算,提醒我们在利用运算律时要注意什么呢?
例2(1)×(—8) (2)15×(—+)-24×(—)
思考:对于带分数的相关计算我们要注意什么呢?
【盘点收获】
1.乘法法交律:两个数相乘,交换因数位置,积不变,即:(用含有字母的式子表达)
2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相等,积不变,即:(用含有字母的式子表达)
3.乘法分配律:一个数同两个数的和相乘,等于把这个数分别同两个加数相乘,再把积相加.即:(用含有字母的式子表达)
【自我检测】
1.-的倒数是 ,倒数等于本身的数是
2.乘积为-1的数叫做互为负倒数,则-2的负倒数是( )
A.-1 B.- C. D.1
3.a、b互为相反数,c、d互为负倒数,则a十b+cd=
4.计算(-7.5)×(—)+(-7.5)×-(—7.5)×6=
5.利用分配律计算时,正确的方案可以是 ( )
A . B.
C . D .
6.计算:
(1) (2)
(3) (4)
(5) (6)
(7) (8)
运河初级中学“学讲计划”导学案
2.6有理数乘法与除法(3)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.会将有理数的除法转化成乘法
2.会进行有理数的乘除混合运算
【自主感知】
1.问题
某周每天上午8时的气温记录如下:
星期一 星期二 星期三 星期四 星期五 星期六 星期日
-3℃ -2℃ -3℃ 0℃ -2℃ -1℃ -3℃
这周每天上午8时的平均气温为多少?
2.思考
你怎样计算上述结果?有几种方法?
对于这一算式小丽和小明有两种算法:
因为 (-2)×7= -14
所以 (-14)÷7= -2
除法是乘法的逆运算 除以一个数等于乘这个数的倒数
请你比较他们的算法是否都正确?你能根据他们的算法总结出有理数除法的规律吗?
这个规律是:
【展示交流】
例1 计算
(1) 36÷(-9) (2) (-48)÷(-6)
(3) (-32)÷4×(-8) (4) 17×(-6)÷(-5)
体会:
对于两个整数的除法可采用直接除的办法,先确定 的符号,再把 相除.
例2
(1) (2)
体会:如果除数是分数,常常利用除以一个数等于 倒数,把除法转化为乘法,如果有理数乘除混合运算,往往先把除法转化为乘法,然后按照乘法法则确定积的符号,最后求出结果.
【盘点收获】
1.有理数除法则(1):除以一个不等于0的数,等于乘以这个数的倒数.字母表示为a÷b=a×
2.有理数除法法则(2):两数相除,同号得正、异号得负、并把绝对值相除.0除以任何一个不等于0的数,都得0
【自我检测】
1.若,则的值不可能为 ( )
A.0 B.1 C.2 D.-2
2.-的倒数是 ,两个非零有理数的和为0,则它们的商为 .
3.若则 0;若则 0.
4.两个有理数和除以这两个有理数的积,其商等于0,则这两个有理数( )
A.互为倒数 B.有一个数是0
C.互为相反数 D.互为相反数,且都不为零.
5.计算:
⑴ (2)
(3) (4)-8 ÷ (一)÷ (一)
(5)
运河初级中学“学讲计划”导学案
2.7有理数的乘方 (1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1.知道有理数乘方的实际含义并能进行有理数乘方的运算
【自主感知】
1.算一算
手工拉面是我国的传统面食.制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣,如此反复操作,连续扣六七次后便成了许多细细的面条.假如一拉扣了6次,你能算出一共有多少根面条吗
2.做一做
(1)将一张纸对折再对折(纸不得撕裂),直到无法对折为止.猜猜看,这时纸有几层
(2)对折1次纸变成2层,对折2次纸变成4层,依此类推,每对折1次层数就增加1倍.你折了多少次 请用算式表示你对折出来的纸层数.
【展示交流】
例1 计算:(1) 26 (2)62
(3)(-3)4 (4)-34
(5)(-4)3 (6)-43
想一想:(1)与(2)结果一样吗?(3)与(4)结果一样吗?(5)与(6)结果一样吗?为什么?
例2 (1) (2) (3) (4)
想一想:1.(2)与(4)它们相同吗?为什么?
例3(1) (2) (3) (4)
议一议:观察一下幂的符号,看看有何规律性的东西呢?
练一练
(1)________________的平方等于9; -14+1=_____
(2)(-4)2底数是______指数是______(-4)2=_______
(3) 34表示___个___ 相乘; (-2)3=______ ; 12003 -(- 1)2002=_______
(4) 一个数的平方为它本身,这个数是 ;
一个数的立方为它本身,这个数是
【盘点收获】
正数的任何次幂都是 ;负数的 幂是负数, 幂是正数;零的 幂都是零.任何一个数的偶次幂都是 数
【自我检测】
1.对于式子(-4)3,正确的说法是 ( )
A.-4是底数,3是冪 B.4是底数,3是冪
C. .4是底数,3是指数 D. -4是底数,3是指数
2.118表示 ( )
A.11个8相乘 B.11乘以8 C.8个11相乘 D.8个11相加
3.一个数的平方一定是 ( )
A.正数 B.负数 C.非正数 D.非负数
4.计算(-1)2002+(-1)2003的值等于 ( )
A.0 B.1 C.-1 D.2
5.如果一个有理数的偶次幂是非负数,那么这个数是( )
A.正数 B.负数 C.非负数 D.任何有理数
6. = ,—= ,= ,—= 。
7.平方等于64的数是 ,立方等于64的数是 。
8.计算
(1) (-6)2 (2) (3)
(4) (5) (6)
(7) (8)
运河初级中学“学讲计划”导学案
2.7 有理数的乘方 (2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
会用科学记数法表示比较大的数
【自主感知】
1.回顾
(1)什么叫乘方?什么叫幂;指出an中的指数、底数、幂
(2)计算32+42= ___________;(2)______________;
-32+(-3)2+(-0.5)3=_____________.
(3)“练一练”
10=10( )
100=10×10( )
1 000 =10×10×10=10( )
10 000=10×10×10×10=10( )
________ =________ =105
2.问题
光的速度大约是300 000 000米/秒;地球半径约为6400000米;赤道长约为40000000米;地球表面积约为:510000000000000平方米。
(1)上面各资料都有出现较大的数,这些数在记录的过程中非常容易出错,你能想办法使得我们记录得又快又准吗?
3.感知
一般地,一个大于10的数可以表示成a×10n 的形式,其中1≤a<10, n是正整数,这种记数方法叫做科学记数法
注意:把一个大于10的数可以写成a×10n时,必须遵循
① ②
【展示交流】
例1 1972年3月发射的“先驱者10号”,是人类发往太阳系外的第一艘人造太空探测器.至2003年2月人们最后一次收到它发回的信号时,它已飞离地球12200000000km.用科学记数法表示这个距离.
例2 请用科学记数法表示696 000;1 000 000; 58 000
【盘点收获】
1.科学记数法:把一个大于10的数表示成a×10n的形式,其中a是数位只有一位的整数,即1≤a<10,n是正整数,这种记数方法叫科学记数法.
2.科学记数法a×10n中n的确定:n为整数部分的位数减1.
3.用科学计数法表示一个比较大的数时,有两点要注意:
① ②
【自我检测】
1.用科学记数法记出下列各数:
(1) 7 000 000; (2) 92 000; (3) 63 000 000; (4) 304 000;
(5) 8 700 000; (6) 500 900 000;(7)374.2 (8) 7000.5.
2.下列用科学记数法记出的数,写出原数.
(1)2×106= (2)9.6×105= (3)7.58×107= ;
(4)6.03×108= (5)5.002×107= (6)5.016×102=
3.我国西部地区面积约为640万平方千米,用科学记数法表示为( )
A.640×104平方千米 B.6.4×106平方千米
C.64×105平方千米 D.4×107平方千米
4. 2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为( )
A.3.1×106元 B.3.11×104元 C.3.1×104元 D.3.10×105元
5.用科学记数法记出下列各数:
(1)地球离太阳约有一亿五千万千米;
(2)地球上煤的储量估计为15万亿吨以上;
(3)月球的质量约是7 340 000 000 000 000万吨;
运河初级中学“学讲计划”导学案
2.8有理数的混合运算(1)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1. 知道有理数的混合运算顺序,正确熟练地进行有理数的混合运算;
2.学会在计算前认真审题,确定运算顺序,计算中按步骤审慎进行,最后要验算的好习惯.
【自主感知】
1.指出下列各题的运算顺序:
(1)6÷3×2;
本题含有 种运算,应先算 ,再算 ;
(2)6÷;
本题含有 种运算,还含有 ,应先算 ,再算 ;
比较(1)(2)的运算顺序,你能得到什么结论?
_____________________________________________________________________________
(3)17-8÷+4×;本题含有 种运算,应先算 ,
再算 ;
(4)32-50÷22×+1;本题含有 种运算,应先算 ,再算 ;
然后再算 。
【展示交流】
例1 (1)计算: 8-23÷×
(2) 计算: 9+5×-2÷4
(3)3×[2-]-300÷5;
例2
(1)2×[-+ eq \b(-)]-2÷4;
(2) eq \b(--)÷ eq \b(-)+2×;
(3)-2×- eq \b(+3)÷3+ eq \b(+22)÷3-2×
【盘点收获】
对于有理数的混合运算,正确的运算顺序是:先 ,再 ,最后 .如果有括号,先算 .对于同一级运算,应按 顺序依次运算
【自我检测】
1.⑴(2×3)2= ;⑵2×32= ;⑶2+32= ;⑷(2+3)2=
2. -42= ;(-4)2= ;-5-9+16=
3.若ab互为相反数,mn互为倒数,则2(a+b)+3mn=
4.计算8÷(-4)×2的结果是( )
A.-4 B.-1 C.-16 D.4
5.-22+(-2)2+(-2)3+23的结果是( )
A.-8 B.0 C.8 D.24
5.计算
(1)-1× eq \b(1-)÷1 (2)[12-4×]÷4
(3)2×3-4×+15 (4)-14-×[2―2]
(5)-8-3×3―4 (6)-3-[-5+ eq \b(1-0.2×)÷]
运河初级中学“学讲计划”导学案
2.8有理数的混合运算(2)
七年级 班 姓名 日期 编写:冯君柏 审核:闫怀恩
【学习目标】
1. 熟练地进行有理数的加、减、乘、除、乘方及混合运算;
2.运用有关运算律简化有理数的运算.
【自主感知】
1.回顾
(1)1÷2-2×3 (2)-1-[1-]
2. 试用两种不同的方法计算,并回答问题
eq \b(--)÷ eq \b(-)+ eq \b(-)
解法一: 解法二:
你认为哪一种方法简便?为什么?从中能得到什么启示?
【展示交流】
例1 计算: eq \b(-)×3÷3× eq \b(-)
例2 eq \b(-)÷ eq \b(-)+2×
【盘点收获】
1.有理数的混合运算顺序是先算 ,再算 ,最后算 ,如果有括号,要先算括号里的.
2.在有理数混合运算中,加法、乘法的所有运算律都能用;选择适当的运算律可以使计算简便.
【自我检测】
1.计算= ;-5+28÷(-2)×(-14)=
(-2)2+〔18-(-3)×2〕÷4= .
2.下列计算正确的是( )
A.(-1)4×(-1)3 B.2×32=62=36 C. D.
3.计算-2×32―(―2×32)=( )
A.0 B.-54 C.-72 D.-18
4.计算:
⑴ ⑵
⑶ ⑷
第2次对折
第3次对折
第1次对折
PAGE
1
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
