19.2.2菱形的性质[下学期]
文档属性
| 名称 | 19.2.2菱形的性质[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 542.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-22 20:00:00 | ||
图片预览





文档简介
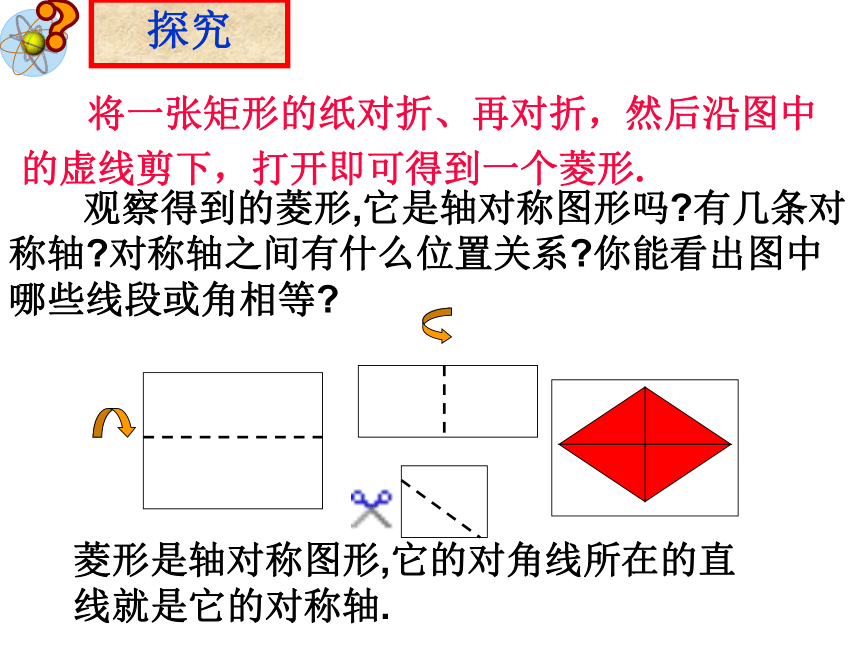
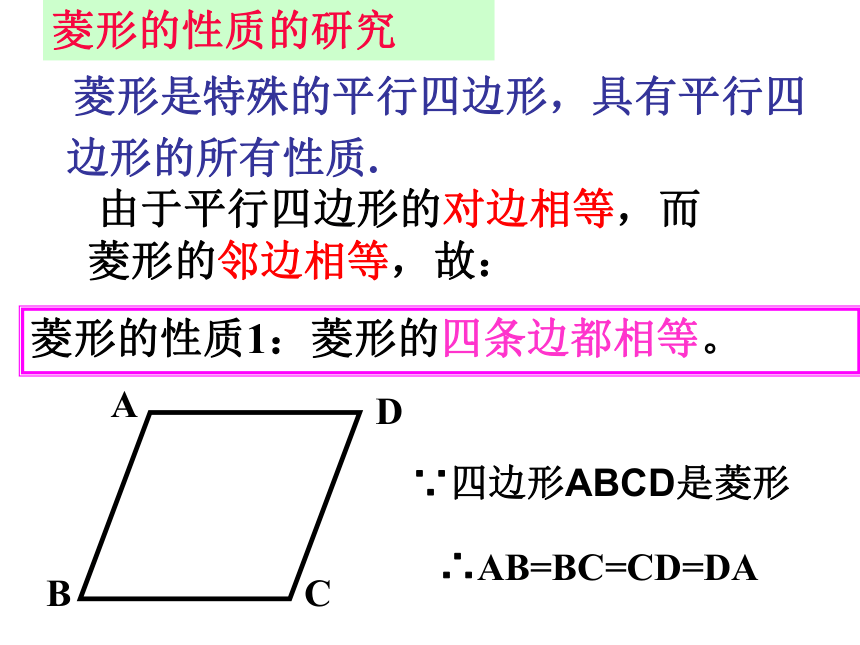
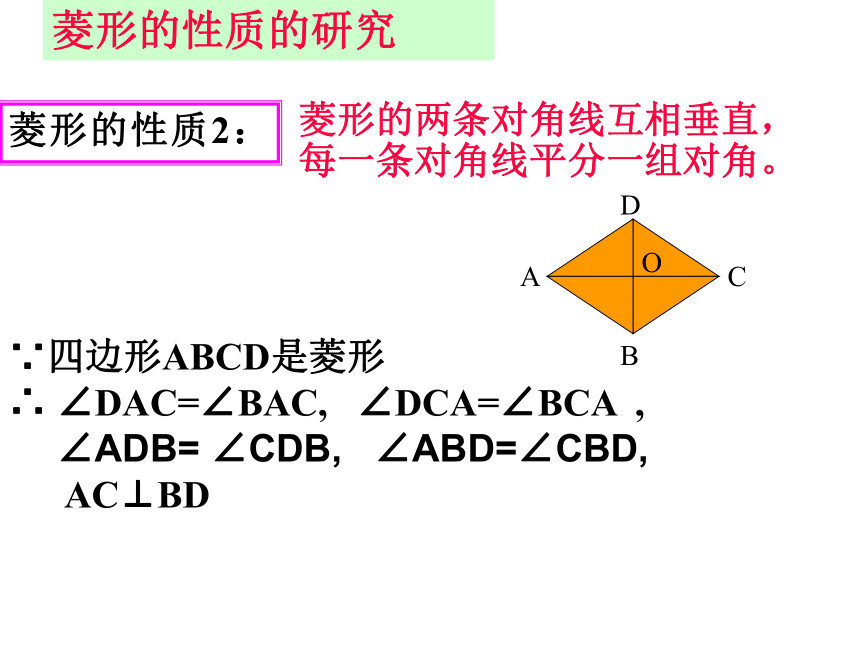
课件22张PPT。19.2.2 菱形观察平行四边形菱形菱形:有一组邻边相等的平行四边形叫做菱形. 将一张矩形的纸对折、再对折,然后沿图中的虚线剪下,打开即可得到一个菱形.探究菱形是轴对称图形,它的对角线所在的直线就是它的对称轴. 观察得到的菱形,它是轴对称图形吗?有几条对称轴?对称轴之间有什么位置关系?你能看出图中哪些线段或角相等? 由于平行四边形的对边相等,而菱形的邻边相等,故:菱形的性质1:菱形的四条边都相等。 菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质的研究∵四边形ABCD是菱形∴AB=BC=CD=DA菱形的两条对角线互相垂直,每一条对角线平分一组对角。菱形的性质2:菱形的性质的研究∵四边形ABCD是菱形
∴ ∠DAC=∠BAC, ∠DCA=∠BCA ,
∠ADB= ∠CDB, ∠ABD=∠CBD,
AC⊥BD 性质:角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分对称性中心对称图形角边线对称性中心对称图形,轴对称图形菱形的对边平行,四条边相等菱形的两组对角分别相等菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积:S菱形=底×高=对角线乘积的一半例1 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2).∴花坛的两条小路长AC=2AO=20(m)BD=2BO≈34.64(m).1、四边形ABCD是菱形,O是两条对角线的
交点,已知AB=5cm,AO=4cm,求对角
线AC、BD的长。解:∵四边形ABCD是菱形AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543∴AC=2OA=8cm
BD=2OB ⒉菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )A.10cm B.7cm
C. 5cm D.4cm34C3.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B4.如图,菱形ABCD的边长为4cm,∠BAD=1200。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。。解:菱形ABCD 中,∵ ∠BAD=12005.菱形ABCD的周长为16,相邻两角的度数比为1:2.⑴求菱形ABCD的对角线的长;⑵求菱形ABCD的面积.6.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。课后练习1,菱形具有而矩形不一定具有的特性是:两条对角线每一条对角线_____;各边_____;
2.菱形的周长是44CM则它的边长是_____.
3,菱形的两个邻角之比为1:2,周长为4A,则短对角线的长为____.
4,下列图形中不是中心对称图形的是( )
A菱形 B平行四边形 C等边三角形 D圆
5,从菱形的钝角顶点向对边作垂线,如果垂线平分对边,则菱形的四个角的度数为( )试试你自己1,如图,已知菱形对角线长分别为12CM和16CM,求菱形的高.
ABCDOE2,已知菱形的一条对角线为16一条边为10求菱形的积.两组对边
分别平行矩形有一个角是直角菱形有一组邻边相等
∴ ∠DAC=∠BAC, ∠DCA=∠BCA ,
∠ADB= ∠CDB, ∠ABD=∠CBD,
AC⊥BD 性质:角边线平行四边形的对角相等.平行四边形的对边平行且相等平行四边形的对角线互相平分对称性中心对称图形角边线对称性中心对称图形,轴对称图形菱形的对边平行,四条边相等菱形的两组对角分别相等菱形的两条对角线互相垂直平分,每一条对角线平分一组对角。相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678【菱形的面积公式】OES菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积:S菱形=底×高=对角线乘积的一半例1 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2).∴花坛的两条小路长AC=2AO=20(m)BD=2BO≈34.64(m).1、四边形ABCD是菱形,O是两条对角线的
交点,已知AB=5cm,AO=4cm,求对角
线AC、BD的长。解:∵四边形ABCD是菱形AC⊥BD∴∴OB=3∴ BD=2OB=6 cm543∴AC=2OA=8cm
BD=2OB ⒉菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )A.10cm B.7cm
C. 5cm D.4cm34C3.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )A.75°B.60°C.45°D.30°B4.如图,菱形ABCD的边长为4cm,∠BAD=1200。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。。解:菱形ABCD 中,∵ ∠BAD=12005.菱形ABCD的周长为16,相邻两角的度数比为1:2.⑴求菱形ABCD的对角线的长;⑵求菱形ABCD的面积.6.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。课后练习1,菱形具有而矩形不一定具有的特性是:两条对角线每一条对角线_____;各边_____;
2.菱形的周长是44CM则它的边长是_____.
3,菱形的两个邻角之比为1:2,周长为4A,则短对角线的长为____.
4,下列图形中不是中心对称图形的是( )
A菱形 B平行四边形 C等边三角形 D圆
5,从菱形的钝角顶点向对边作垂线,如果垂线平分对边,则菱形的四个角的度数为( )试试你自己1,如图,已知菱形对角线长分别为12CM和16CM,求菱形的高.
ABCDOE2,已知菱形的一条对角线为16一条边为10求菱形的积.两组对边
分别平行矩形有一个角是直角菱形有一组邻边相等
