有理数
图片预览


文档简介
教 案 首 页
教材版本 人教版 学段 七年级(上) 学科 数学
章节 1.2.1 课题名 有理数 课时 1课时
执教教师单位 南昌一中 教师姓名 贺得剑
教学目标 通过本节的学习使学生掌握有理数的概念,并且能熟练地进行有理数的分类,进而感受到数学的分类思想在数学运用.
教学重点 有理数的概念和分类
教学难点 有理数的分类
教具 多媒体
时间安排 1、引入新课、讲授新课 15′2、例题讲解一、课堂练习一 10′3、例题讲解二、课堂练习二 10′4、课堂练习三 、小结 10′
课后小结 在讲解有理数的概念时,能做到由几个例子到一般概念;在理解有理数的分类时,要能分几种情况;在结合例题讲解有理数的概念时,还可以做到更细致一点;探究题选择的较好,对学生在掌握有理数的概念之后的提高有一定的帮助.
教学方法:应用多媒体进行启发式教学,做到讲练结合
组织教学:12人为一班,一班又平均分成两个小组
教学过程:
(一)引入新课
想一想
你所知道的数可以分成哪些种类?你是按照什么划分的?
正整数,如:1,2,3,……;零,0;
负整数,如:-1,-2,-3,……;
正分数,如: , 0.1,5.32,……;
负分数,如:-0.5, ,-150.25,…….
所有正整数组成正整数集合,所有负整数组成负整数集合.
想一想:0.1,5.32,-0.5,-150.25等为什么被列为分数呢?
(二)讲授新课 (写在黑板上)
正整数、零、负整数统称为整数.
正分数、负分数统称为分数.
整数和分数统称为有理数.
想一想:有理数可以怎样分类呢?
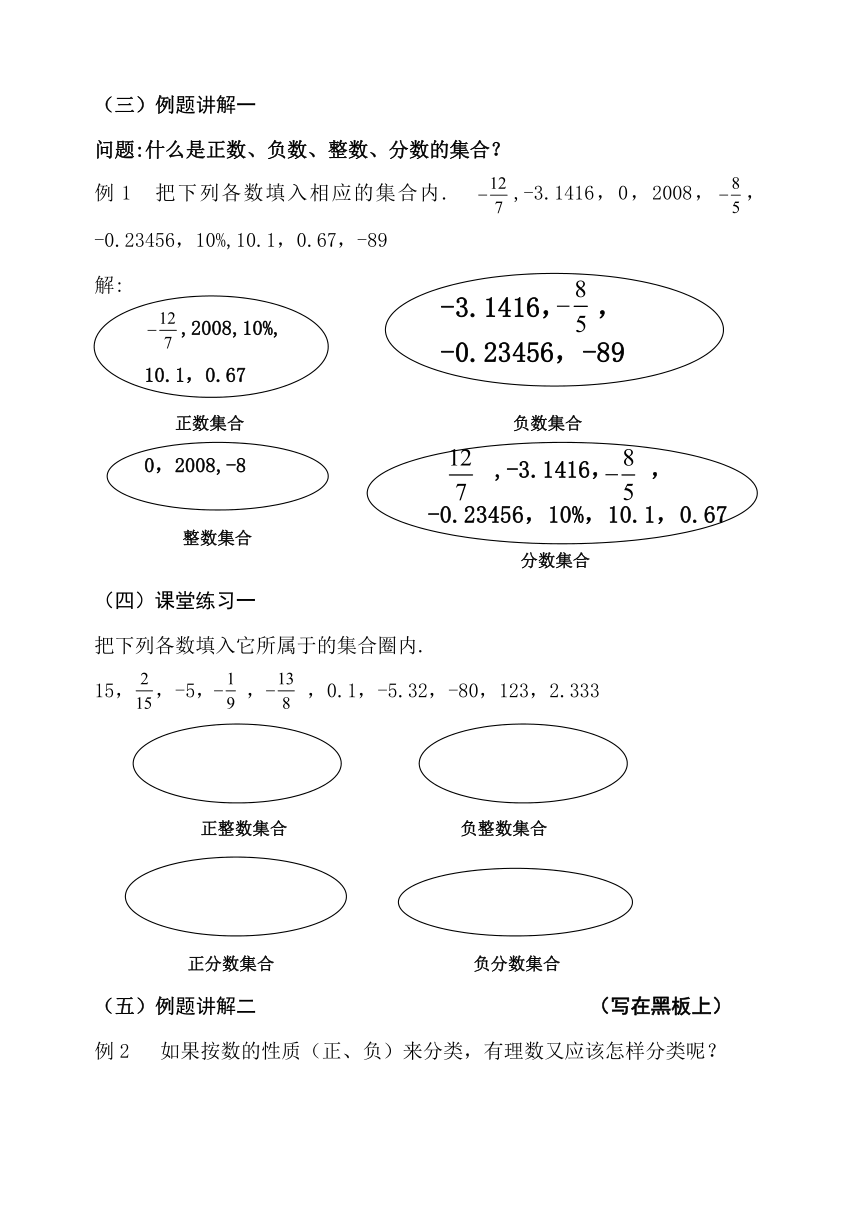
(三)例题讲解一
问题:什么是正数、负数、整数、分数的集合?
例1 把下列各数填入相应的集合内. ,-3.1416,0,2008,,-0.23456,10%,10.1,0.67,-89
解:
,2008,10%,
10.1,0.67
0,2008,-8
(四)课堂练习一
把下列各数填入它所属于的集合圈内.
15, ,-5, , ,0.1,-5.32,-80,123,2.333
(五)例题讲解二 (写在黑板上)
例2 如果按数的性质(正、负)来分类,有理数又应该怎样分类呢?
把所有的正数组成的集叫 正数集合 .
(六)课堂练习二
以下是两位同学给出的有理数的分类方法,你认为他们的分类正确吗 ?
(七)课堂练习三
1、判断下列各题是否正确:
(1)0是整数(√ )
(2)自然数一定是整数( √ )
(3)0一定是正整数(× )
(4)整数一定是自然数(× )
2、下列关于零的说法,正确的有( B )
①0是最小的正整数 ②0是最小的有理数
③0不是负数 ④0既是非正数也是非负数
A、1个 B、2个 C、3个 D、4个
3、简答题: (写在黑板上)
(1)-1和0之间还有负数吗?如有请列举.
(2)-3和-1之间有负整数吗?-2和2之间有哪些整数?
(3)有比-1大的负整数吗?有比1小的正整数吗?
(4)写出大于-105小于-100的所有整数.
答:(1)有如:-0.1,-0.2等.
(2)有如:-2;-1,0,1.
(3)没有;也没有.
(4)-104,-103,-102,-101.
探究题: (写在黑板上)
1、如果用一个字母表示一个数,那么a可能是什么样的数?一定是正数吗?-a就一定是负数吗?
答:不一定,a可能是正数,可能是负数,也可能是0,–a也一样.
2、图中两个圆圈分别表示正整数集合和整数集合, 你能说出这个重叠部分表示什么数的集合吗
答:正整数集合.
(八)小 结
这节课我们的收获:
1、有理数的概念;
2、有理数的分类;
3、数学方法:分类思想.
(九)家庭作业 P17/习题1.2/1 P18/6
板书设计
有
理
数
整数
分数
正整数
零
负整数
正分数
负分数
-3.1416, ,
-0.23456,-89
负数集合
正数集合
,-3.1416, ,
-0.23456,10%,10.1,0.67
整数集合
分数集合
正整数集合
负整数集合
负分数集合
正分数集合
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
正数
负数
答:不正确,忘了还有零.
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
答:不正确,分类没有标准.
整数集合
…
…
正数集合
…
1.2.1 有 理 数
课堂练习一
课堂练习二
探究题:
整数:
分数:
有理数:
分类:
教材版本 人教版 学段 七年级(上) 学科 数学
章节 1.2.1 课题名 有理数 课时 1课时
执教教师单位 南昌一中 教师姓名 贺得剑
教学目标 通过本节的学习使学生掌握有理数的概念,并且能熟练地进行有理数的分类,进而感受到数学的分类思想在数学运用.
教学重点 有理数的概念和分类
教学难点 有理数的分类
教具 多媒体
时间安排 1、引入新课、讲授新课 15′2、例题讲解一、课堂练习一 10′3、例题讲解二、课堂练习二 10′4、课堂练习三 、小结 10′
课后小结 在讲解有理数的概念时,能做到由几个例子到一般概念;在理解有理数的分类时,要能分几种情况;在结合例题讲解有理数的概念时,还可以做到更细致一点;探究题选择的较好,对学生在掌握有理数的概念之后的提高有一定的帮助.
教学方法:应用多媒体进行启发式教学,做到讲练结合
组织教学:12人为一班,一班又平均分成两个小组
教学过程:
(一)引入新课
想一想
你所知道的数可以分成哪些种类?你是按照什么划分的?
正整数,如:1,2,3,……;零,0;
负整数,如:-1,-2,-3,……;
正分数,如: , 0.1,5.32,……;
负分数,如:-0.5, ,-150.25,…….
所有正整数组成正整数集合,所有负整数组成负整数集合.
想一想:0.1,5.32,-0.5,-150.25等为什么被列为分数呢?
(二)讲授新课 (写在黑板上)
正整数、零、负整数统称为整数.
正分数、负分数统称为分数.
整数和分数统称为有理数.
想一想:有理数可以怎样分类呢?
(三)例题讲解一
问题:什么是正数、负数、整数、分数的集合?
例1 把下列各数填入相应的集合内. ,-3.1416,0,2008,,-0.23456,10%,10.1,0.67,-89
解:
,2008,10%,
10.1,0.67
0,2008,-8
(四)课堂练习一
把下列各数填入它所属于的集合圈内.
15, ,-5, , ,0.1,-5.32,-80,123,2.333
(五)例题讲解二 (写在黑板上)
例2 如果按数的性质(正、负)来分类,有理数又应该怎样分类呢?
把所有的正数组成的集叫 正数集合 .
(六)课堂练习二
以下是两位同学给出的有理数的分类方法,你认为他们的分类正确吗 ?
(七)课堂练习三
1、判断下列各题是否正确:
(1)0是整数(√ )
(2)自然数一定是整数( √ )
(3)0一定是正整数(× )
(4)整数一定是自然数(× )
2、下列关于零的说法,正确的有( B )
①0是最小的正整数 ②0是最小的有理数
③0不是负数 ④0既是非正数也是非负数
A、1个 B、2个 C、3个 D、4个
3、简答题: (写在黑板上)
(1)-1和0之间还有负数吗?如有请列举.
(2)-3和-1之间有负整数吗?-2和2之间有哪些整数?
(3)有比-1大的负整数吗?有比1小的正整数吗?
(4)写出大于-105小于-100的所有整数.
答:(1)有如:-0.1,-0.2等.
(2)有如:-2;-1,0,1.
(3)没有;也没有.
(4)-104,-103,-102,-101.
探究题: (写在黑板上)
1、如果用一个字母表示一个数,那么a可能是什么样的数?一定是正数吗?-a就一定是负数吗?
答:不一定,a可能是正数,可能是负数,也可能是0,–a也一样.
2、图中两个圆圈分别表示正整数集合和整数集合, 你能说出这个重叠部分表示什么数的集合吗
答:正整数集合.
(八)小 结
这节课我们的收获:
1、有理数的概念;
2、有理数的分类;
3、数学方法:分类思想.
(九)家庭作业 P17/习题1.2/1 P18/6
板书设计
有
理
数
整数
分数
正整数
零
负整数
正分数
负分数
-3.1416, ,
-0.23456,-89
负数集合
正数集合
,-3.1416, ,
-0.23456,10%,10.1,0.67
整数集合
分数集合
正整数集合
负整数集合
负分数集合
正分数集合
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
正数
负数
答:不正确,忘了还有零.
有理数
正有理数
负有理数
正整数
正分数
负整数
负分数
有
理
数
正数
整数
分数
负数
零
答:不正确,分类没有标准.
整数集合
…
…
正数集合
…
1.2.1 有 理 数
课堂练习一
课堂练习二
探究题:
整数:
分数:
有理数:
分类:
