弦切角定理[上学期]

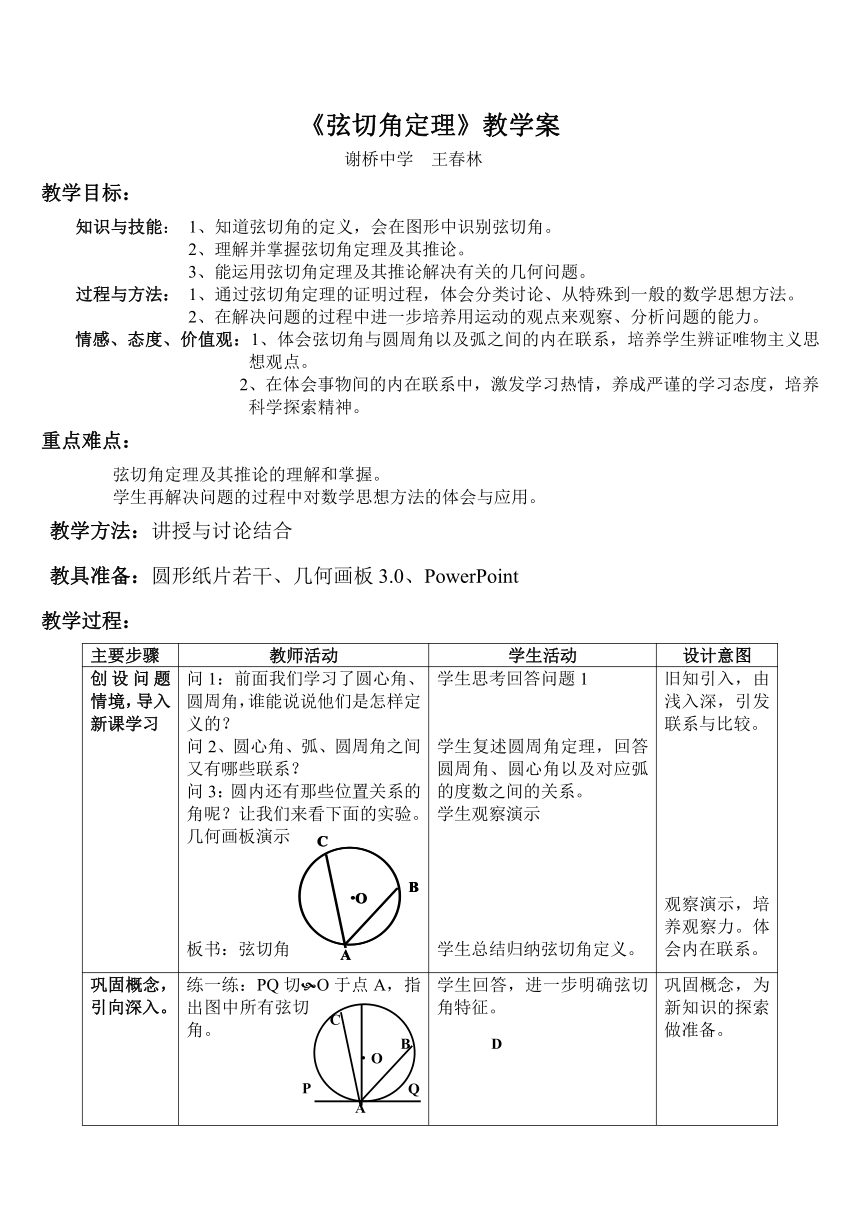
《弦切角定理》教学案
谢桥中学 王春林
教学目标：
知识与技能： 1、知道弦切角的定义，会在图形中识别弦切角。
2、理解并掌握弦切角定理及其推论。
3、能运用弦切角定理及其推论解决有关的几何问题。
过程与方法： 1、通过弦切角定理的证明过程，体会分类讨论、从特殊到一般的数学思想方法。
2、在解决问题的过程中进一步培养用运动的观点来观察、分析问题的能力。
情感、态度、价值观：1、体会弦切角与圆周角以及弧之间的内在联系，培养学生辨证唯物主义思想观点。
2、在体会事物间的内在联系中，激发学习热情，养成严谨的学习态度，培养科学探索精神。
重点难点：
弦切角定理及其推论的理解和掌握。
学生再解决问题的过程中对数学思想方法的体会与应用。
教学方法：讲授与讨论结合
教具准备：圆形纸片若干、几何画板3.0、PowerPoint
教学过程：
主要步骤 教师活动 学生活动 设计意图
创设问题情境，导入新课学习 问1：前面我们学习了圆心角、圆周角，谁能说说他们是怎样定义的？问2、圆心角、弧、圆周角之间又有哪些联系？问3：圆内还有那些位置关系的角呢？让我们来看下面的实验。几何画板演示板书：弦切角 学生思考回答问题1学生复述圆周角定理，回答圆周角、圆心角以及对应弧的度数之间的关系。学生观察演示学生总结归纳弦切角定义。 旧知引入，由浅入深，引发联系与比较。观察演示，培养观察力。体会内在联系。
巩固概念，引向深入。 练一练：PQ切O于点A，指出图中所有弦切角。 学生回答，进一步明确弦切角特征。 巩固概念，为新知识的探索做准备。
问4：我们在学习圆周角定理时，是怎样证明的？问5：请同学们也将上图的弦切角分分类，在练习本上画出来，并说一说你是怎样分类的？问6：指出你画的弦切角所夹的弧，各有何特征： 学生：根据圆周角与圆心的关系分为三类。学生操作，交流分类方法。回答问题。学生回答。 类比后分类，让学生对弦切角的认识进一步加深，渗透分类讨论思想。
探索弦切角定理，经历发现过程。 猜想：在各图中画出夹弧所对的圆周角，大胆想一想，说出你的结论。指导学生依次证明上述情况。问7：根据弦切角定理，若两弦切角所夹弧相等，弦切角又怎样？ 学生操作，猜想：弦切角等于它所夹的弧所对的圆周角。学生在教师指导下完成证明学生回答：推论：若两弦切角所夹弧相等，弦切角也相等。 让学生经历操作—猜想—探索—发现的全过程，激发求知欲望，体会从特殊到一般的数学思想方法，体验数学成功，获得发现的快乐。
巩固应用，体验成功。 例1如图：已知AB是O的直径，AC是弦，直线CE和O切于点C，AD⊥CE垂足为D。求证：AC平分∠BAD。 B ●O AE C D例2如图：已知ABC内接于O，D为BC中点，过D作O的切线与AB的延长线相交于E点。求证：（1）DE∥BC；（2）BD2=BE·AC。 A B C E D 师生互动，共同完成该例的证明。师生互动，共同完成。 初步应用，通过基本图形的构造，强化方法的把握，融新知于旧知。本例的给出在于启迪学生对知识的综合运用，在新的高度把握知识。
归纳小结，总结升华，提高认识。 准确区分弦切角于圆周角、圆心角的区别与联系，正确运用弦切角定理。学会“从特殊到一般，再从一般到特殊”的研究问题的数学思想方法。 学生归纳弦切角、弦、弧间的区别与联系。 帮助学生总结提升理性认识。
布置作业 如图：已知O的内接四边形ABCD，∠C=1300，AD为O的直径，过B作O的切线BE。求：∠ABE的度数。 A O D C B E2、如图：已知PA、PB切O于点A和E，PCB为O的割线，∠BAC的平分线交BC于D点。求证：PE=PD。 A O P C B D E 学生完成作业 教师个别指导
教后记
C
A
B
·
O
O
·
B
A
C
C
B
P
Q
A
D
·O