有趣的平衡(课件)人教版六年级下册(共17张PPT)
文档属性
| 名称 | 有趣的平衡(课件)人教版六年级下册(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 18:57:19 | ||
图片预览




文档简介
(共17张PPT)
人教版六年级下册第六单元综合与实践
1.你玩过跷跷板吗?
2.你觉得跷跷板和平衡有什么关系呢?
有 趣 的 平 衡
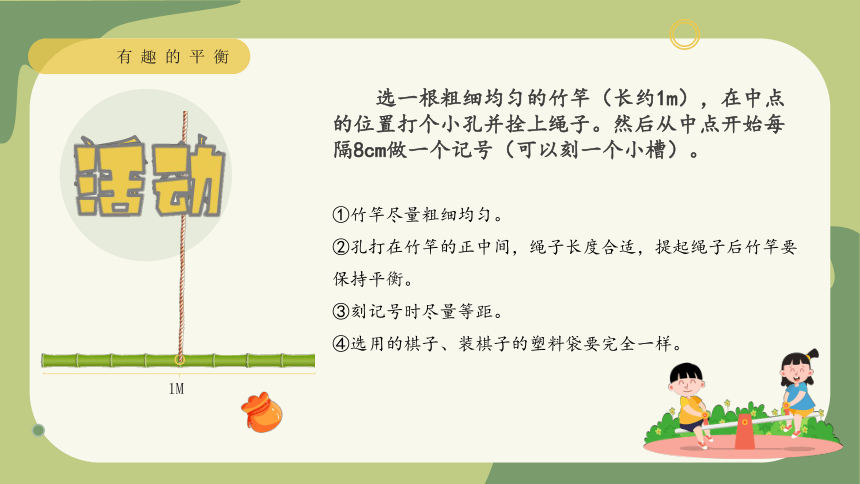
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
①竹竿尽量粗细均匀。
②孔打在竹竿的正中间,绳子长度合适,提起绳子后竹竿要保持平衡。
③刻记号时尽量等距。
④选用的棋子、装棋子的塑料袋要完全一样。
有 趣 的 平 衡
1M
活动
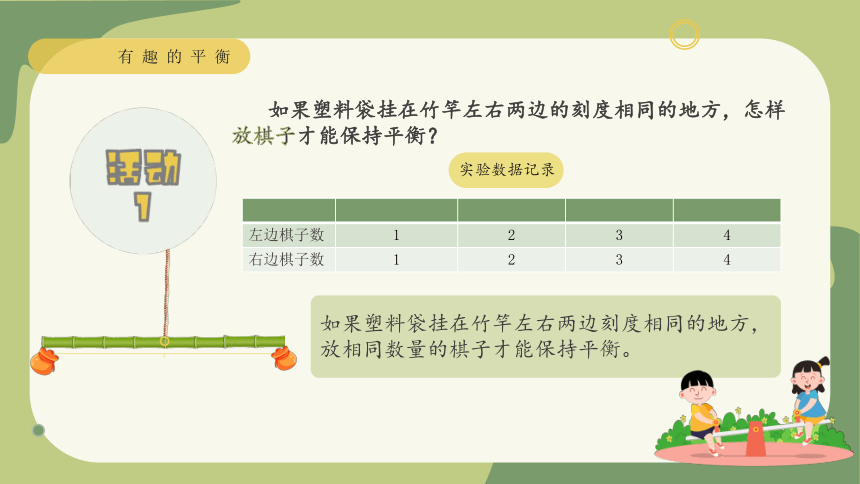
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
有 趣 的 平 衡
实验数据记录
左边棋子数 1 2 3 4
右边棋子数 1 2 3 4
如果塑料袋挂在竹竿左右两边刻度相同的地方,
放相同数量的棋子才能保持平衡。
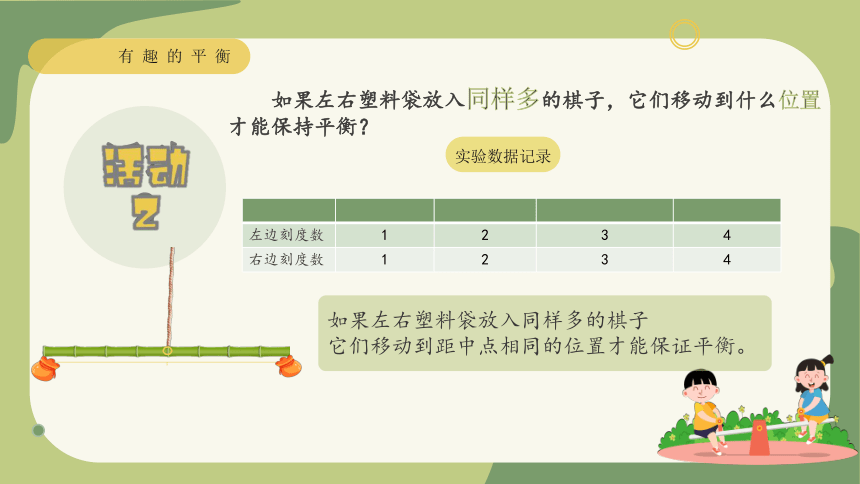
如果左右塑料袋放入同样多的棋子,它们移动到什么位置才能保持平衡?
有 趣 的 平 衡
实验数据记录
左边刻度数 1 2 3 4
右边刻度数 1 2 3 4
如果左右塑料袋放入同样多的棋子
它们移动到距中点相同的位置才能保证平衡。
活动
2
活动
3
左边的塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上放几个才能保证平衡?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
3 4 4 3
活动
3
如果左边的塑料袋在刻度6上,放1个棋子,右边的塑料袋在刻度3上,放几个才能保持平衡?在刻度2上呢?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
6 1 3 2
6 1 2 3
活动
3
根据实验数据,你有什么发现?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
3 4 4 3
6 1 3 2
6 1 2 3
左边刻度数×左边棋子数=右边刻度数×右边棋子数
竹杆才能保证平衡
活动
4
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子才能保证平衡呢?
有 趣 的 平 衡
6 5 4 3 2 1 0 1 2 3 4 5 6
3个
棋子
左 刻 度 1 2 3 4 6
所放棋子数
乘 积
从表中你发现刻度数和所放棋子数成什么比例关系?
12 6 4 3 2
12 12 12 12 12
母女二人玩跷跷板,体重12千克的女儿坐在距离支点15分米的地方。如果母亲体重是60千克,那么她要坐在距离支点多远的地方才能保持跷跷板平衡?
有 趣 的 平 衡
左边刻度数×棋子数=右边刻度数×棋子数
解:设她要坐在x分米的地方才能保持跷跷板平衡。
60x=12×15
x=3
答:她要坐在3分米的地方才能保持跷跷板平衡。
有 趣 的 平 衡
解:设B物体重为Xg,
3x=180×4
x=240
答:B物体重为240g。
A =180g
B =
O
如果竹竿左右两边拴上重物A和B,竹竿平衡。已知A物体重180g,B物体重多少克
根据木棒左侧放棋子的数量和位置,想一想:在木棒右侧什么位置放几个棋子,才能保证木棒平衡?共有几种方案?
有 趣 的 平 衡
左边 右边
刻度数 棋子数 刻度数 棋子数
3 6 1 12
2 9
3 6
6 3
9 2
6个
棋子
4 3 2 1 0 1 2 3 4 5 6 7 8 9 10
有 趣 的 平 衡
同学们经常玩的跷跷板,有时能够达到左右平衡,就是应用了杠杆原理。像下图那样,用一根硬的棍子,借助一个支点,一个人能把一块大石头撬起来,这也是运用了杠杆原理。像这样的棍子,就是杠杆,你还能举出一些生活中应用杠杆原理的例子吗?
思考
有 趣 的 平 衡
名言
给我一个支点,我就可以撬起地球。
——力学之父阿基米德
拓展
有 趣 的 平 衡
生活中的杠杆原理
总结
有 趣 的 平 衡
1.如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
2.如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
3.左边刻度数×棋子数=右边刻度数×棋子数,杠杆才能保证平衡。
4.当左边棋子数×左刻度的积不变时,右边棋子数与右刻度成反比例。
人教版六年级下册第六单元综合与实践
人教版六年级下册第六单元综合与实践
1.你玩过跷跷板吗?
2.你觉得跷跷板和平衡有什么关系呢?
有 趣 的 平 衡
选一根粗细均匀的竹竿(长约1m),在中点的位置打个小孔并拴上绳子。然后从中点开始每隔8cm做一个记号(可以刻一个小槽)。
①竹竿尽量粗细均匀。
②孔打在竹竿的正中间,绳子长度合适,提起绳子后竹竿要保持平衡。
③刻记号时尽量等距。
④选用的棋子、装棋子的塑料袋要完全一样。
有 趣 的 平 衡
1M
活动
如果塑料袋挂在竹竿左右两边的刻度相同的地方,怎样放棋子才能保持平衡?
有 趣 的 平 衡
实验数据记录
左边棋子数 1 2 3 4
右边棋子数 1 2 3 4
如果塑料袋挂在竹竿左右两边刻度相同的地方,
放相同数量的棋子才能保持平衡。
如果左右塑料袋放入同样多的棋子,它们移动到什么位置才能保持平衡?
有 趣 的 平 衡
实验数据记录
左边刻度数 1 2 3 4
右边刻度数 1 2 3 4
如果左右塑料袋放入同样多的棋子
它们移动到距中点相同的位置才能保证平衡。
活动
2
活动
3
左边的塑料袋在刻度3上,放4个棋子,右边的塑料袋在刻度4上放几个才能保证平衡?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
3 4 4 3
活动
3
如果左边的塑料袋在刻度6上,放1个棋子,右边的塑料袋在刻度3上,放几个才能保持平衡?在刻度2上呢?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
6 1 3 2
6 1 2 3
活动
3
根据实验数据,你有什么发现?
有 趣 的 平 衡
实验数据记录
左边 右边
刻度数 棋子数 刻度数 棋子数
3 4 4 3
6 1 3 2
6 1 2 3
左边刻度数×左边棋子数=右边刻度数×右边棋子数
竹杆才能保证平衡
活动
4
左边在刻度4上放3个棋子并保持不变,右边分别在各个刻度上放几个棋子才能保证平衡呢?
有 趣 的 平 衡
6 5 4 3 2 1 0 1 2 3 4 5 6
3个
棋子
左 刻 度 1 2 3 4 6
所放棋子数
乘 积
从表中你发现刻度数和所放棋子数成什么比例关系?
12 6 4 3 2
12 12 12 12 12
母女二人玩跷跷板,体重12千克的女儿坐在距离支点15分米的地方。如果母亲体重是60千克,那么她要坐在距离支点多远的地方才能保持跷跷板平衡?
有 趣 的 平 衡
左边刻度数×棋子数=右边刻度数×棋子数
解:设她要坐在x分米的地方才能保持跷跷板平衡。
60x=12×15
x=3
答:她要坐在3分米的地方才能保持跷跷板平衡。
有 趣 的 平 衡
解:设B物体重为Xg,
3x=180×4
x=240
答:B物体重为240g。
A =180g
B =
O
如果竹竿左右两边拴上重物A和B,竹竿平衡。已知A物体重180g,B物体重多少克
根据木棒左侧放棋子的数量和位置,想一想:在木棒右侧什么位置放几个棋子,才能保证木棒平衡?共有几种方案?
有 趣 的 平 衡
左边 右边
刻度数 棋子数 刻度数 棋子数
3 6 1 12
2 9
3 6
6 3
9 2
6个
棋子
4 3 2 1 0 1 2 3 4 5 6 7 8 9 10
有 趣 的 平 衡
同学们经常玩的跷跷板,有时能够达到左右平衡,就是应用了杠杆原理。像下图那样,用一根硬的棍子,借助一个支点,一个人能把一块大石头撬起来,这也是运用了杠杆原理。像这样的棍子,就是杠杆,你还能举出一些生活中应用杠杆原理的例子吗?
思考
有 趣 的 平 衡
名言
给我一个支点,我就可以撬起地球。
——力学之父阿基米德
拓展
有 趣 的 平 衡
生活中的杠杆原理
总结
有 趣 的 平 衡
1.如果塑料袋挂在竹竿左右两边刻度相同的地方,放相同数量的棋子才能保持平衡。
2.如果左右塑料袋放入同样多的棋子,它们移动到距中点相同的位置才能保证平衡。
3.左边刻度数×棋子数=右边刻度数×棋子数,杠杆才能保证平衡。
4.当左边棋子数×左刻度的积不变时,右边棋子数与右刻度成反比例。
人教版六年级下册第六单元综合与实践
