22.1.4 二次函数y=ax?+bx+c的图象和性质 第2课时 用待定系数法求二次函数的解析式 习题课件
文档属性
| 名称 | 22.1.4 二次函数y=ax?+bx+c的图象和性质 第2课时 用待定系数法求二次函数的解析式 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:36:59 | ||
图片预览








文档简介
(共22张PPT)
22.1.4 二次函数y=ax +bx+c的图象和性质
第2课时 用待定系数法求二次函数的解析式
第二十二章 二次函数
必
●
知识要点全练
夯实基础
知识点1
用“一般式”求二次函数的解析式
1.(杭州中考)已知二次函数y=ax2十4x十c,
当x=一2时,函数值是一1;当x=1时,函
数值是5.则此二次函数的解析式为(A)
A.y=2x2+4x-1
B.y=x2+4x-2
C.y=-2x2+4x+1
D.y=2x2+4x+1
2.已知点A(0,3),B(2,3)是抛物线y=
一x2十bx十c上的两点,则该抛物线的解析
式是y=-x2十2x+3
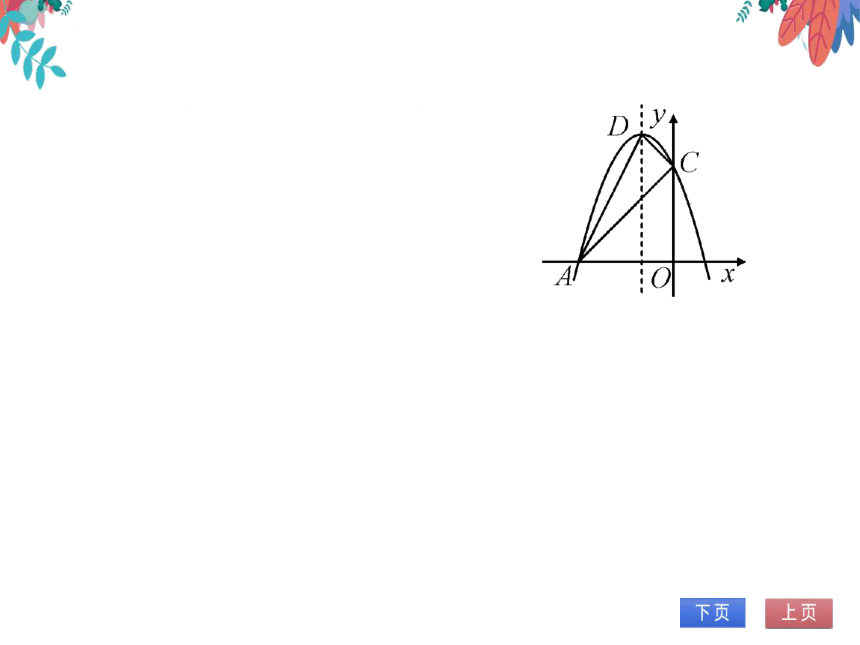
3.如图,抛物线y=一x2十bx十c经过点A(一3,
0)和点C(0,3).
(1)求抛物线所对应的函数解析式,并直接
写出顶点D的坐标;
(2)若过顶点D的直线将△ACD的面积分为
1:2两部分,并与x轴交于点Q,则点Q的
坐标为
-30或(-1,0)
解:(1)把点A(一3,0)和点C(0,
3)的坐标代入y=一x2+bx+
-9一3b十c=0,
C,得
c=3,
b=一2,
解得
C=3,
.y=一x2一2x十3.顶点D的坐标为(一1,4).
知识点2用“顶点式”求二次函数的解析式
4.(云南大理中考)若抛物线y=ax2十bx十c
的顶点是A(2,1),且经过点B(1,0),则抛
物线的函数解析式为
(B)
A.y=x2+4x-3
B.y=-x2+4x-3
C.y=-x2-4x3
D.y=-x2+4x+3
5.设函数y=a(x一h)2十k(a,h,k是实数,
a≠0),当x=1时,y=1;当x=6时,y=6,
则
(B)
A.若h=2,则a0
B.若h=3,则a>0
C.若h=4,则a0
D.若h=5,则a0
6.已知二次函数的图象经过点(4,一3),且当
x=3时,y有最大值一1,则这个二次函数
的解析式为y=一2(x一3)2一1.
7.已知抛物线y=ax2+bx十c的对称轴是直
线x=1,且经过点A(3,0)和点B(2,一3),
求这条抛物线的解析式.
解:,抛物线y=x2+bx+c的对称轴是直线
x=1,∴.y=a.x2十bx+c=a(x-1)2+k.
把点A(3,0),B(2,一3)代入得
4a+k=0,.a=1,
a十k=一3,k=一4.
'.这条抛物线的解析式为y=(x一1)2一4
或y=x2一2x一3.
22.1.4 二次函数y=ax +bx+c的图象和性质
第2课时 用待定系数法求二次函数的解析式
第二十二章 二次函数
必
●
知识要点全练
夯实基础
知识点1
用“一般式”求二次函数的解析式
1.(杭州中考)已知二次函数y=ax2十4x十c,
当x=一2时,函数值是一1;当x=1时,函
数值是5.则此二次函数的解析式为(A)
A.y=2x2+4x-1
B.y=x2+4x-2
C.y=-2x2+4x+1
D.y=2x2+4x+1
2.已知点A(0,3),B(2,3)是抛物线y=
一x2十bx十c上的两点,则该抛物线的解析
式是y=-x2十2x+3
3.如图,抛物线y=一x2十bx十c经过点A(一3,
0)和点C(0,3).
(1)求抛物线所对应的函数解析式,并直接
写出顶点D的坐标;
(2)若过顶点D的直线将△ACD的面积分为
1:2两部分,并与x轴交于点Q,则点Q的
坐标为
-30或(-1,0)
解:(1)把点A(一3,0)和点C(0,
3)的坐标代入y=一x2+bx+
-9一3b十c=0,
C,得
c=3,
b=一2,
解得
C=3,
.y=一x2一2x十3.顶点D的坐标为(一1,4).
知识点2用“顶点式”求二次函数的解析式
4.(云南大理中考)若抛物线y=ax2十bx十c
的顶点是A(2,1),且经过点B(1,0),则抛
物线的函数解析式为
(B)
A.y=x2+4x-3
B.y=-x2+4x-3
C.y=-x2-4x3
D.y=-x2+4x+3
5.设函数y=a(x一h)2十k(a,h,k是实数,
a≠0),当x=1时,y=1;当x=6时,y=6,
则
(B)
A.若h=2,则a0
B.若h=3,则a>0
C.若h=4,则a0
D.若h=5,则a0
6.已知二次函数的图象经过点(4,一3),且当
x=3时,y有最大值一1,则这个二次函数
的解析式为y=一2(x一3)2一1.
7.已知抛物线y=ax2+bx十c的对称轴是直
线x=1,且经过点A(3,0)和点B(2,一3),
求这条抛物线的解析式.
解:,抛物线y=x2+bx+c的对称轴是直线
x=1,∴.y=a.x2十bx+c=a(x-1)2+k.
把点A(3,0),B(2,一3)代入得
4a+k=0,.a=1,
a十k=一3,k=一4.
'.这条抛物线的解析式为y=(x一1)2一4
或y=x2一2x一3.
同课章节目录
