第22章 二次函数 专题训练(四) 二次函数与几何综合 习题课件
文档属性
| 名称 | 第22章 二次函数 专题训练(四) 二次函数与几何综合 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:36:59 | ||
图片预览




文档简介
(共19张PPT)
专题训练(四) 二次函数与几何综合
第二十二章 二次函数
必
●
类型1
图形面积问题
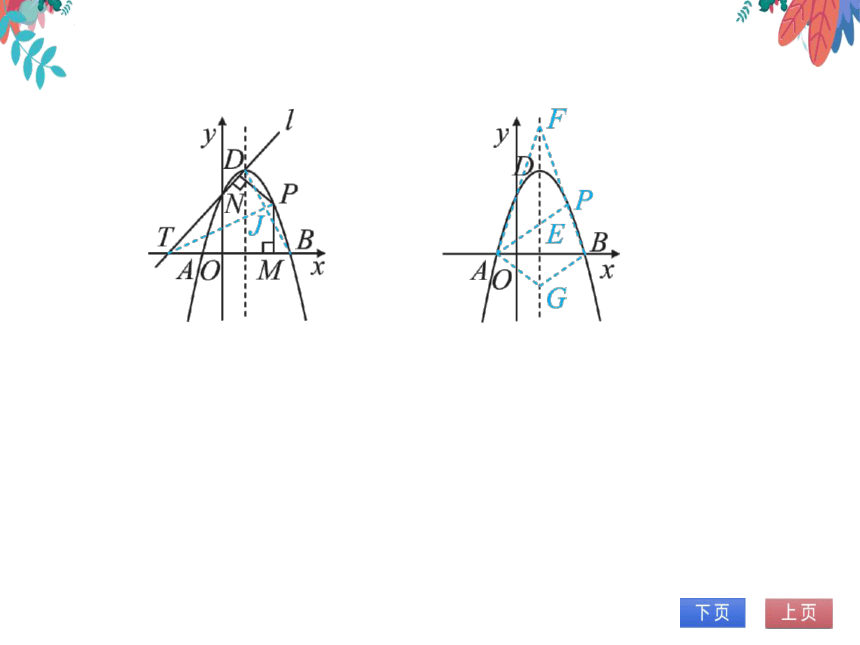
1.(2022·山东淄博)如图,抛物线y=一x2十
b十c与x轴相交于A,B两点(点A在点B的
左侧),顶点D(1,4)在直线1:y=
rr北,动
点P(m,n)在x轴上方的抛物线上.
(1)求这条抛物线对应的函数表达式;
(2)过点P作PMx轴于点M,PN⊥L于点
V,当1(3)设直线AP,BP与抛物线的对称轴分
别相交于点E,F,请探索以A,F,B,G
(G是点E关于x轴的对称点)为顶点
的四边形面积是否随着P点的运动而
发生变化,若不变,求出这个四边形的
面积;若变化,说明理由.
M
X
(1)解:,抛物线的顶点为D(1,4),.抛物线的解析式为y
=-(x-1)2+4=一x2+2x+3;
(2)解:如图,设直线1交x轴于点T,连接PT,BD,BD交
PM于点J,设P(m,-m+2m+3),点D(1,4),.
S四边形mBP最大时,PM十PN的值最大,直线BD的解析式为
y=-2x十6,.J(m,-2m+6),.PJ=-m2+4m-3,
S四边形mr=Sms十S0P=一m2十4m十7=一(m一2)2十11,
m=2时,S四边形Br最大,最大值为11,.PM十PN的最
大值=
22
(3)解:四边形AFBG的面积不变,理由:如图,设P(m,一
m+2m+3),.A(一1,0),B(3,0),.直线AP的解析式
为y=一(m一3)x-m+3,.E(1,-2m+6),.E,G关于
K轴对称,.G(1,2m一6),.直线PB的解析式为y=一
(m+1)x+3(m+1),.'.F(1,2m+2),.'.GF=2m+2-(2m
一6=8,四边形FBG的面积=号×ABX FG=2X4
2
X8=16,..四边形AFBG的面积是定值.
类型2角度问题
2.(2022,过宁会山)如图,抛物线y-一2十
bx十c与x轴交于A(一1,0),B两点,与y
轴交于点C(0,2),连接BC.
(1)求抛物线的解析式;
(2)点P是第三象限抛物线上一点,直线
PB与y轴交于点D,△BCD的面积为
12,求点P的坐标;
(3)在(2)的条件下,若点E是线段BC上
的一个动点,连接OE,将△OEB沿直
线OE翻折得到△OEB,当直线EB与
直线BP相交所成锐角为45°时,直接
写出点B的坐标.
专题训练(四) 二次函数与几何综合
第二十二章 二次函数
必
●
类型1
图形面积问题
1.(2022·山东淄博)如图,抛物线y=一x2十
b十c与x轴相交于A,B两点(点A在点B的
左侧),顶点D(1,4)在直线1:y=
rr北,动
点P(m,n)在x轴上方的抛物线上.
(1)求这条抛物线对应的函数表达式;
(2)过点P作PMx轴于点M,PN⊥L于点
V,当1
别相交于点E,F,请探索以A,F,B,G
(G是点E关于x轴的对称点)为顶点
的四边形面积是否随着P点的运动而
发生变化,若不变,求出这个四边形的
面积;若变化,说明理由.
M
X
(1)解:,抛物线的顶点为D(1,4),.抛物线的解析式为y
=-(x-1)2+4=一x2+2x+3;
(2)解:如图,设直线1交x轴于点T,连接PT,BD,BD交
PM于点J,设P(m,-m+2m+3),点D(1,4),.
S四边形mBP最大时,PM十PN的值最大,直线BD的解析式为
y=-2x十6,.J(m,-2m+6),.PJ=-m2+4m-3,
S四边形mr=Sms十S0P=一m2十4m十7=一(m一2)2十11,
m=2时,S四边形Br最大,最大值为11,.PM十PN的最
大值=
22
(3)解:四边形AFBG的面积不变,理由:如图,设P(m,一
m+2m+3),.A(一1,0),B(3,0),.直线AP的解析式
为y=一(m一3)x-m+3,.E(1,-2m+6),.E,G关于
K轴对称,.G(1,2m一6),.直线PB的解析式为y=一
(m+1)x+3(m+1),.'.F(1,2m+2),.'.GF=2m+2-(2m
一6=8,四边形FBG的面积=号×ABX FG=2X4
2
X8=16,..四边形AFBG的面积是定值.
类型2角度问题
2.(2022,过宁会山)如图,抛物线y-一2十
bx十c与x轴交于A(一1,0),B两点,与y
轴交于点C(0,2),连接BC.
(1)求抛物线的解析式;
(2)点P是第三象限抛物线上一点,直线
PB与y轴交于点D,△BCD的面积为
12,求点P的坐标;
(3)在(2)的条件下,若点E是线段BC上
的一个动点,连接OE,将△OEB沿直
线OE翻折得到△OEB,当直线EB与
直线BP相交所成锐角为45°时,直接
写出点B的坐标.
同课章节目录
