22.3 实际问题与二次函数 第2课时 建立适当的直角坐标系解决实际问题 习题课件
文档属性
| 名称 | 22.3 实际问题与二次函数 第2课时 建立适当的直角坐标系解决实际问题 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
22.3 实际问题与二次函数
第2课时 建立适当的直角坐标系解决
实际问题
第二十二章 二次函数
必
●
知识要点全练
夯实基础
知识点1用二次函数解决拱桥类问题
1.(陕西中考)某景点的“喷水
m
巨龙”口中C处的水流呈抛
物线形,该水流喷出的高度
O A
乃八xfm
y(m)与水平距离x(m)之间
的关系如图所示,D为该水流的最高点,
DA⊥OB,垂足为A.已知OC=OB=8m,
OA=2m,测该水流距水平面的最大高度
AD的长度为
(A)
A.9 m
B.
101
m
C.11m
D.
12m
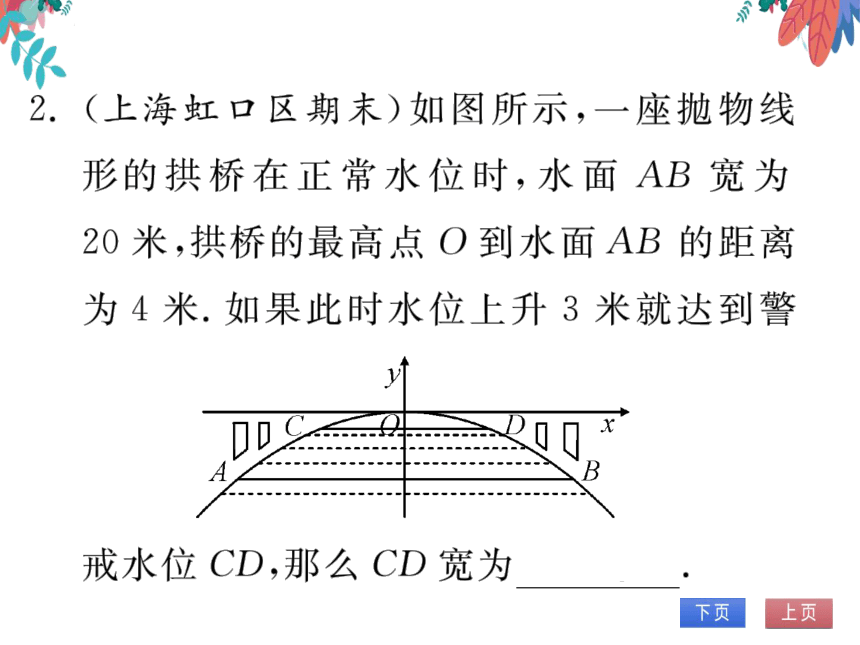
2.(上海虹口区期末)如图所示,一座抛物线
形的拱桥在正常水位时,水面AB宽为
20米,拱桥的最高点O到水面AB的距离
为4米.如果此时水位上升3米就达到警
00
戒水位CD,那么CD宽为10米
3.单行隧道的截面是抛物线形,且抛物线的
解析式为y一名3.25,第车高
3米,宽4米,该车
不能(填“能”或“不
能”)通过隧道.
知识点2
用二次函数知识解决运动问题
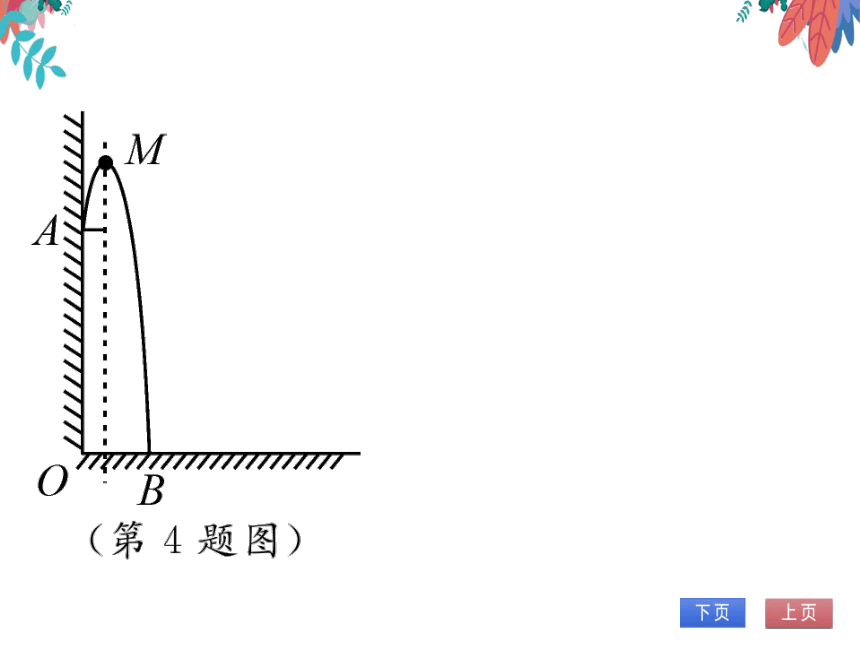
4.如图,从某建筑物10m高的窗口A处用水
管向外喷水,喷出的水呈抛物线状(抛物线
所在平面与墙面垂直),如果抛物线的最高
点离墙1m,离地面
m,则水流落地点
B离墙的距离OB是
(B)
A.2 m
B.3 m
C.4 m
D.5
m
镇艺夜
77X7777777777777777777
B
(第4题图)
5.(2022·徐州一模)北京冬奥会跳台滑雪项
目比赛其标准台高度是90m.运动员起跳
后的飞行路线可以看作是抛物线的一部
分,运动员起跳后的竖直高度y(单位:m)
与水平距离x(单位:)近似满足函数关系
y=ax2十bx十c(a≠0).如图记录了某运动
员起跳后的x与y的三组数据,根据上述
函数模型和数据,可推断出该运动员起跳
后飞行到最高点时,水平距离为
(B)
A.10m
B.15m
C.20m
D.22.5m
y/mt
93.9
90.0
i
i
82.2
●
0
i
0
1
0
1
20
40x/m
(第5题图)
6.(2022·雨花区校级二模)从地面竖直向上抛
出一小球,小球的高度h(单位:m)与小球运动
时间(单位:s)之间的函数关系如图所示.下列
结论:①小球抛出3秒时达到最高点;②小球从
抛出到落地经过的路程是90m;③小球的高度
h=20时,t=1或5.④小球抛出2秒后的高度
是35m.其中正确的有
(A)
22.3 实际问题与二次函数
第2课时 建立适当的直角坐标系解决
实际问题
第二十二章 二次函数
必
●
知识要点全练
夯实基础
知识点1用二次函数解决拱桥类问题
1.(陕西中考)某景点的“喷水
m
巨龙”口中C处的水流呈抛
物线形,该水流喷出的高度
O A
乃八xfm
y(m)与水平距离x(m)之间
的关系如图所示,D为该水流的最高点,
DA⊥OB,垂足为A.已知OC=OB=8m,
OA=2m,测该水流距水平面的最大高度
AD的长度为
(A)
A.9 m
B.
101
m
C.11m
D.
12m
2.(上海虹口区期末)如图所示,一座抛物线
形的拱桥在正常水位时,水面AB宽为
20米,拱桥的最高点O到水面AB的距离
为4米.如果此时水位上升3米就达到警
00
戒水位CD,那么CD宽为10米
3.单行隧道的截面是抛物线形,且抛物线的
解析式为y一名3.25,第车高
3米,宽4米,该车
不能(填“能”或“不
能”)通过隧道.
知识点2
用二次函数知识解决运动问题
4.如图,从某建筑物10m高的窗口A处用水
管向外喷水,喷出的水呈抛物线状(抛物线
所在平面与墙面垂直),如果抛物线的最高
点离墙1m,离地面
m,则水流落地点
B离墙的距离OB是
(B)
A.2 m
B.3 m
C.4 m
D.5
m
镇艺夜
77X7777777777777777777
B
(第4题图)
5.(2022·徐州一模)北京冬奥会跳台滑雪项
目比赛其标准台高度是90m.运动员起跳
后的飞行路线可以看作是抛物线的一部
分,运动员起跳后的竖直高度y(单位:m)
与水平距离x(单位:)近似满足函数关系
y=ax2十bx十c(a≠0).如图记录了某运动
员起跳后的x与y的三组数据,根据上述
函数模型和数据,可推断出该运动员起跳
后飞行到最高点时,水平距离为
(B)
A.10m
B.15m
C.20m
D.22.5m
y/mt
93.9
90.0
i
i
82.2
●
0
i
0
1
0
1
20
40x/m
(第5题图)
6.(2022·雨花区校级二模)从地面竖直向上抛
出一小球,小球的高度h(单位:m)与小球运动
时间(单位:s)之间的函数关系如图所示.下列
结论:①小球抛出3秒时达到最高点;②小球从
抛出到落地经过的路程是90m;③小球的高度
h=20时,t=1或5.④小球抛出2秒后的高度
是35m.其中正确的有
(A)
同课章节目录
