22.1.3 二次函数y=a(x一h)?十k的图象和性质 第3课时 二次函数y=a(x一h)?十k的图象和性质 习题课件
文档属性
| 名称 | 22.1.3 二次函数y=a(x一h)?十k的图象和性质 第3课时 二次函数y=a(x一h)?十k的图象和性质 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
22.1.3 二次函数y=a(x一h) 十k的图象和性质 第3课时二次函数y=a(x一h) 十k的图象和性质
第二十二章 二次函数
必
●
知识要点全练
夯实基础
o0ooooooooooooo00000000000000000000
知识点1二次函数y=a(x一h)2十k的图象
和性质
1.(2022·哈尔滨)抛物线y=2(x+9)2一3
的顶点坐标是
(B)
A.(9,-3)
B.(-9,3)
C.(9,3)
D.(-9,3)
2.(2022·湖南郴州)关于二次函数y=(x一
1)十5,下列说法正确的是
(D)
A.函数图象的开口向下
B.函数图象的顶点坐标是(一1,5)
C.该函数有最大值,是大值是5
D.当x>1时,y随x的增大而增大
3.已知点(-1),(-32必小(-2)都
在函数y=3(x+1)2一2的图象上,则y1,
y2,y3的大小关系是
(C)
A.y1>y2>y3
B.y2>y1>y3
C.y2>y3>y1
D.y3>y1>y2
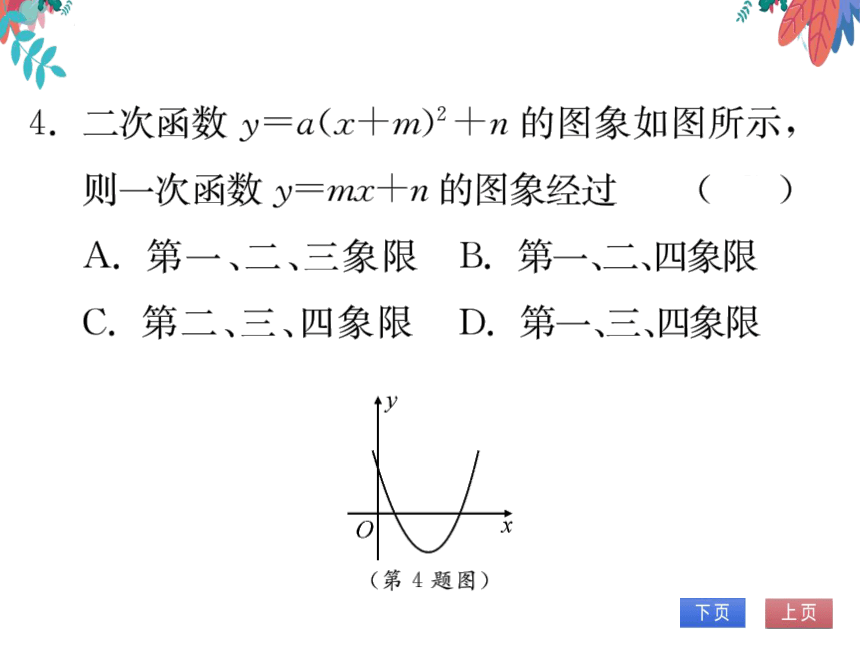
4.二次函数y=a(x十m)2+n的图象如图所示,
则一次函数y=nx十n的图象经过
(C)
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
↑y
0
X
(第4题图)
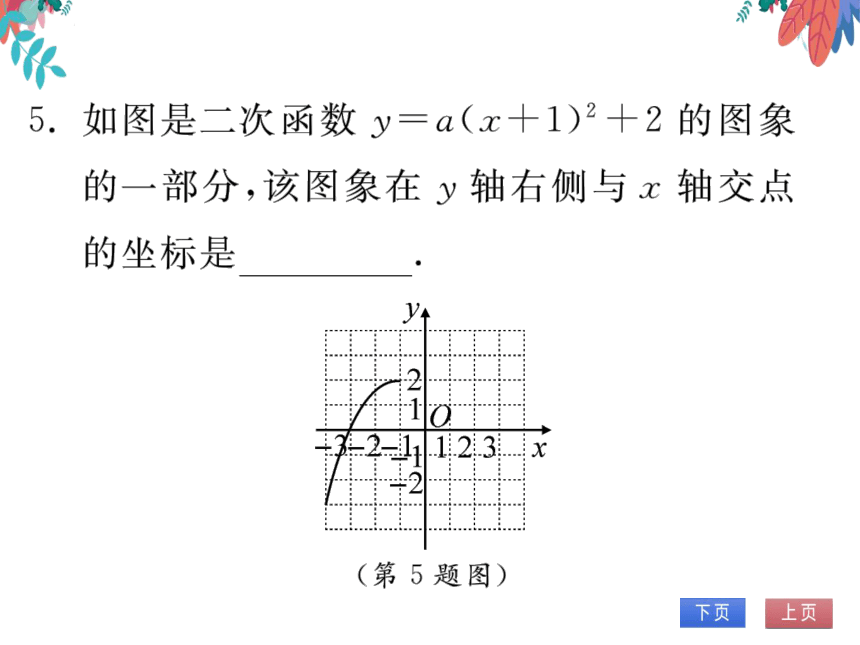
5.如图是二次函数y=a(x十1)2十2的图象
的一部分,该图象在y轴右侧与x轴交点
的坐标是(1,0)
.1.2.3.x
(第5题图)
7.若二次函数y=-(x一m)2十1,当x≤2时,
y随x的增大而增大,则m的取值范围是
m≥2
知识点2二次函数y=a(x一h)2十k与y=
ax2的关系
8.抛物线的函数表达式为y=3(x一2)十1,若
将x轴向上平移2个单位长度,将y轴向左
平移3个单位长度,则该抛物线在新的平面
直角坐标系中的函数表达式为
(C)
A.y=3(x+1)2+3
B.y=3(x-5)2+3
C.y=3(x-5)2-1
D.y=3(x+1)2一1
9.(广西贵港中芳)将如图所示的抛物线向右平
移1个单位长度,再向上平移3个单位长度
后,得到的抛物线的解析式为
A.y=(x-1)2+1
B.y=(x+1)2+1
C.y=2(x-1)2+1
D.y=2(x+1)2+1
10.在平面直角坐标系中,若抛物线y=x2不
动,而把x轴、y轴分别向上、向右平移2
个单位长度,则在新坐标系下,抛物线的
函数解析式为y=(x十2)2一2
22.1.3 二次函数y=a(x一h) 十k的图象和性质 第3课时二次函数y=a(x一h) 十k的图象和性质
第二十二章 二次函数
必
●
知识要点全练
夯实基础
o0ooooooooooooo00000000000000000000
知识点1二次函数y=a(x一h)2十k的图象
和性质
1.(2022·哈尔滨)抛物线y=2(x+9)2一3
的顶点坐标是
(B)
A.(9,-3)
B.(-9,3)
C.(9,3)
D.(-9,3)
2.(2022·湖南郴州)关于二次函数y=(x一
1)十5,下列说法正确的是
(D)
A.函数图象的开口向下
B.函数图象的顶点坐标是(一1,5)
C.该函数有最大值,是大值是5
D.当x>1时,y随x的增大而增大
3.已知点(-1),(-32必小(-2)都
在函数y=3(x+1)2一2的图象上,则y1,
y2,y3的大小关系是
(C)
A.y1>y2>y3
B.y2>y1>y3
C.y2>y3>y1
D.y3>y1>y2
4.二次函数y=a(x十m)2+n的图象如图所示,
则一次函数y=nx十n的图象经过
(C)
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
↑y
0
X
(第4题图)
5.如图是二次函数y=a(x十1)2十2的图象
的一部分,该图象在y轴右侧与x轴交点
的坐标是(1,0)
.1.2.3.x
(第5题图)
7.若二次函数y=-(x一m)2十1,当x≤2时,
y随x的增大而增大,则m的取值范围是
m≥2
知识点2二次函数y=a(x一h)2十k与y=
ax2的关系
8.抛物线的函数表达式为y=3(x一2)十1,若
将x轴向上平移2个单位长度,将y轴向左
平移3个单位长度,则该抛物线在新的平面
直角坐标系中的函数表达式为
(C)
A.y=3(x+1)2+3
B.y=3(x-5)2+3
C.y=3(x-5)2-1
D.y=3(x+1)2一1
9.(广西贵港中芳)将如图所示的抛物线向右平
移1个单位长度,再向上平移3个单位长度
后,得到的抛物线的解析式为
A.y=(x-1)2+1
B.y=(x+1)2+1
C.y=2(x-1)2+1
D.y=2(x+1)2+1
10.在平面直角坐标系中,若抛物线y=x2不
动,而把x轴、y轴分别向上、向右平移2
个单位长度,则在新坐标系下,抛物线的
函数解析式为y=(x十2)2一2
同课章节目录
