第23章 旋转 专题训练(六) 利用旋转进行计算或证明 习题课件
文档属性
| 名称 | 第23章 旋转 专题训练(六) 利用旋转进行计算或证明 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览




文档简介
(共10张PPT)
专题训练(六) 利用旋转进行计算或证明
第二十三章 旋转
必
●
类型1利用旋转进行计算
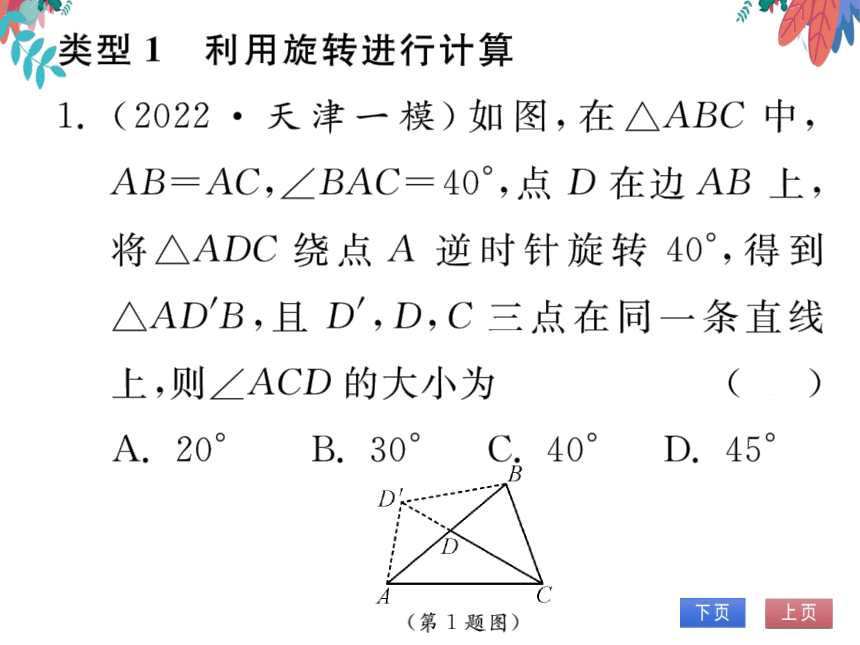
1.(2022·天津一模)如图,在△ABC中,
AB=AC,∠BAC=40°,点D在边AB上,
将△ADC绕点A逆时针旋转40°,得到
△ADB,且D,D,C三点在同一条直线
上,则∠ACD的大小为
B
A.20°
B.30°
C.40°
D.45°
B
t
i
A
C
(第1题图
)
2.(2022春·龙岗区期末)如图,点E是等边三
角形△ABC边AC的中点,点D是直线BC上
一动点,连接ED,并绕点E逆时针旋转90°,得
到线段EF,连接AF若运动过程中AF的最小
值为V3十1,则AB的值为
D
A.2
B.43
C.
D.4
E
B
D
C
(第2题图)
3.(2022·湖北黄石)如图,等边人ABC中,
AB=10,点E为高AD上的一动点,以BE为
边作等边△BEF,连接DF,CF,则∠BCF=
30°
,FB十FD的最小值为5√3
E
D
B
C
(第3题图)
4.(广西梧州中芳)如图,在菱形ABCD中,AB=
2,∠BAD=60°,将菱形ABCD绕点A逆时针方
向旋转,对应得到菱形AEFG,点E在AC上,EF
与CD交于点P,则DP的长是√3一1
G
P
C
A
B
(第4题图)
类型2
利用旋转性质证明
5.(湖南娄底中考)如图,将等腰△ABC绕顶
点B按逆时针方向旋转α角到△A1BC1的
位置,AB与A1C1相交于点D,AC与
A1C1,BC1分别交于点E,F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α时,判定四边形A1BCE的形
状并说明理由.
(1)证明:,人ABC是等腰三角形,
.AB=BC,∠A=∠C.
由题意及旋转的性质知,
B
C
A1B=AB=BC,∠A1=∠A=∠C=∠C,∠ABA1
∠CBC...△BCF≌△BAD(ASA)
(2)解:四边形A1BCE为菱形,理由如下:
由(1)知∠A=∠A1=∠C=∠C1,当∠C=时,则∠A=
∠C1=.又∠ADA1=∠CBC1=a,..∠A=∠ABA1,∠C
=∠CBC..AC∥AB,A,C1∥BC..四边形ABCE是平
行四边形.,AD=BC,.□A1BCE是菱形.
6.(四川南充中考)如图,在矩形ABCD中,
AC=2AB,将矩形ABCD绕点A旋转得到矩形
ABCD',使点B的对应点B落在AC上,BC交
AD于点E,在BC上取点F,使BF=AB.
(1)求证:AE=CE;
(2)求∠FBB的度数;
(3)已知AB=2,求BF的长.
专题训练(六) 利用旋转进行计算或证明
第二十三章 旋转
必
●
类型1利用旋转进行计算
1.(2022·天津一模)如图,在△ABC中,
AB=AC,∠BAC=40°,点D在边AB上,
将△ADC绕点A逆时针旋转40°,得到
△ADB,且D,D,C三点在同一条直线
上,则∠ACD的大小为
B
A.20°
B.30°
C.40°
D.45°
B
t
i
A
C
(第1题图
)
2.(2022春·龙岗区期末)如图,点E是等边三
角形△ABC边AC的中点,点D是直线BC上
一动点,连接ED,并绕点E逆时针旋转90°,得
到线段EF,连接AF若运动过程中AF的最小
值为V3十1,则AB的值为
D
A.2
B.43
C.
D.4
E
B
D
C
(第2题图)
3.(2022·湖北黄石)如图,等边人ABC中,
AB=10,点E为高AD上的一动点,以BE为
边作等边△BEF,连接DF,CF,则∠BCF=
30°
,FB十FD的最小值为5√3
E
D
B
C
(第3题图)
4.(广西梧州中芳)如图,在菱形ABCD中,AB=
2,∠BAD=60°,将菱形ABCD绕点A逆时针方
向旋转,对应得到菱形AEFG,点E在AC上,EF
与CD交于点P,则DP的长是√3一1
G
P
C
A
B
(第4题图)
类型2
利用旋转性质证明
5.(湖南娄底中考)如图,将等腰△ABC绕顶
点B按逆时针方向旋转α角到△A1BC1的
位置,AB与A1C1相交于点D,AC与
A1C1,BC1分别交于点E,F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α时,判定四边形A1BCE的形
状并说明理由.
(1)证明:,人ABC是等腰三角形,
.AB=BC,∠A=∠C.
由题意及旋转的性质知,
B
C
A1B=AB=BC,∠A1=∠A=∠C=∠C,∠ABA1
∠CBC...△BCF≌△BAD(ASA)
(2)解:四边形A1BCE为菱形,理由如下:
由(1)知∠A=∠A1=∠C=∠C1,当∠C=时,则∠A=
∠C1=.又∠ADA1=∠CBC1=a,..∠A=∠ABA1,∠C
=∠CBC..AC∥AB,A,C1∥BC..四边形ABCE是平
行四边形.,AD=BC,.□A1BCE是菱形.
6.(四川南充中考)如图,在矩形ABCD中,
AC=2AB,将矩形ABCD绕点A旋转得到矩形
ABCD',使点B的对应点B落在AC上,BC交
AD于点E,在BC上取点F,使BF=AB.
(1)求证:AE=CE;
(2)求∠FBB的度数;
(3)已知AB=2,求BF的长.
同课章节目录
