23.1 图形的旋转 第1课时 旋转的概念和性质 习题课件
文档属性
| 名称 | 23.1 图形的旋转 第1课时 旋转的概念和性质 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:36:59 | ||
图片预览





文档简介
(共19张PPT)
23.1 图形的旋转
第1课时旋转的概念和性质
第二十三章 旋转
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
旋转的概念
1.如图,△ABC和△ADE均为等边三角形,
则图中可以看成是旋转关系的三角形是
(C)
A.∧ABC和∧ADEB.∧ABC和人ABD
C.△ABD和△ACED.∧ACE和人ADE
知识点2旋转的性质
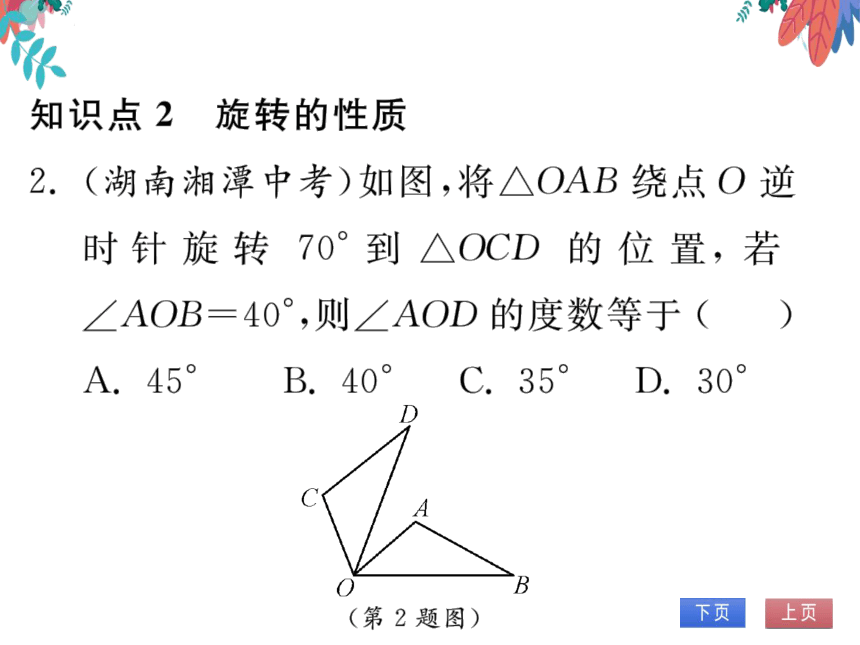
2.(湖南湘潭中芳)如图,将△OAB绕点O逆
时针旋转70°到△OCD的位置,若
∠AOB=40°,则∠AOD的度数等于(D)
A.45°
B.40°
C.35°
D.30°
D
C
A
O
B
(第2题图)
3.(2022·天津)如图,在△ABC中,AB=
AC,若M是BC边上任意一点,将△ABM
绕点A逆时针旋转得到△ACV,点M的对
应点为点N,连接MN,则下列结论一定正
确的是
(C)
A.AB-AN
B.AB∥VC
C.∠AMN=∠ACND.MN⊥AC
N
C
M
A
B
(第3题图)
B
B
A
(第4题图)
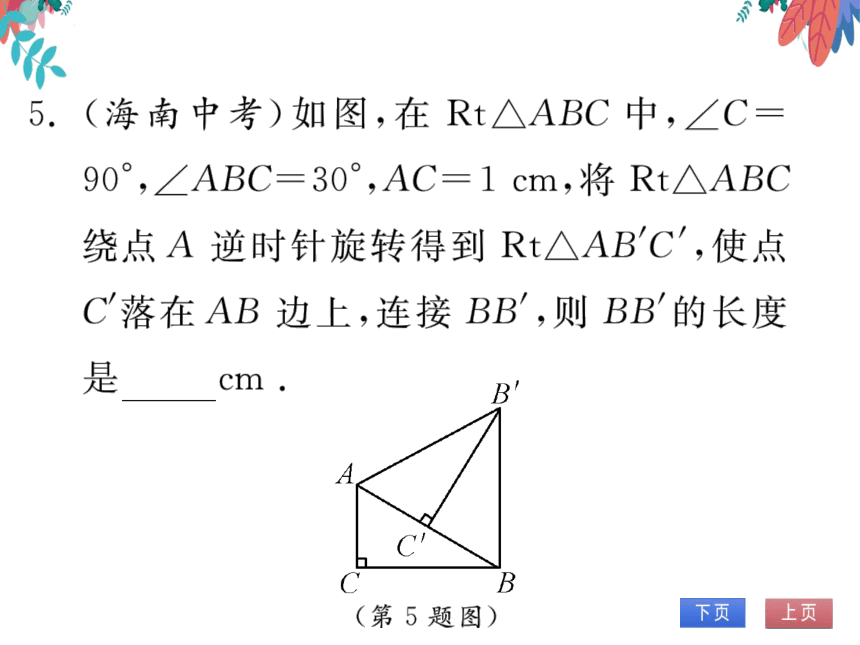
5.(海南中芳)如图,在Rt△ABC中,∠C=
90°,∠ABC=30°,AC=1cm,将Rt△ABC
绕点A逆时针旋转得到Rt△ABC',使点
C落在AB边上,连接BB,则BB的长度
是2
cm
A
C
C
B
(第5题图)
6.(2022春·镇平县期末)如图,在平面直角
坐标系中,边长为√/5的正方形ABCD的顶
点A在x轴正半轴上,C在第一象限,将正
方形ABCD绕点A旋转,当D的坐标为
(3,2)时,则C点的坐标是(5,3)·
C
D
B
0
A
X
(第6题图)
7.如图,在△ABC中,AB=BC,点O是
△ABC内一点,将△ABO旋转后能与
△BCD重合.
(1)旋转中心是点
B
(2)若∠ACB=70°,则旋转角为
40°
(3)若∠ACB=60°,请判断△BOD的形状
并说明理由.
规律方法全练
提升能力
8.(2022春·米脂县期末)如图,点P是等边
三角形ABC内部一点,连接AP、BP、CP,
且AP2=BP2十CP2,现将△APC绕点A
顺时针旋转到△ADB的位置,对于下列结
论:①△ADP是等边三角形;②△ABP≌
△CBP;
③∠DBP=90°;④∠BDA十
∠BPA=210°.其中正确的结论有
(C)
A.1个
B.2个
C.3个
D.4个
23.1 图形的旋转
第1课时旋转的概念和性质
第二十三章 旋转
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1
旋转的概念
1.如图,△ABC和△ADE均为等边三角形,
则图中可以看成是旋转关系的三角形是
(C)
A.∧ABC和∧ADEB.∧ABC和人ABD
C.△ABD和△ACED.∧ACE和人ADE
知识点2旋转的性质
2.(湖南湘潭中芳)如图,将△OAB绕点O逆
时针旋转70°到△OCD的位置,若
∠AOB=40°,则∠AOD的度数等于(D)
A.45°
B.40°
C.35°
D.30°
D
C
A
O
B
(第2题图)
3.(2022·天津)如图,在△ABC中,AB=
AC,若M是BC边上任意一点,将△ABM
绕点A逆时针旋转得到△ACV,点M的对
应点为点N,连接MN,则下列结论一定正
确的是
(C)
A.AB-AN
B.AB∥VC
C.∠AMN=∠ACND.MN⊥AC
N
C
M
A
B
(第3题图)
B
B
A
(第4题图)
5.(海南中芳)如图,在Rt△ABC中,∠C=
90°,∠ABC=30°,AC=1cm,将Rt△ABC
绕点A逆时针旋转得到Rt△ABC',使点
C落在AB边上,连接BB,则BB的长度
是2
cm
A
C
C
B
(第5题图)
6.(2022春·镇平县期末)如图,在平面直角
坐标系中,边长为√/5的正方形ABCD的顶
点A在x轴正半轴上,C在第一象限,将正
方形ABCD绕点A旋转,当D的坐标为
(3,2)时,则C点的坐标是(5,3)·
C
D
B
0
A
X
(第6题图)
7.如图,在△ABC中,AB=BC,点O是
△ABC内一点,将△ABO旋转后能与
△BCD重合.
(1)旋转中心是点
B
(2)若∠ACB=70°,则旋转角为
40°
(3)若∠ACB=60°,请判断△BOD的形状
并说明理由.
规律方法全练
提升能力
8.(2022春·米脂县期末)如图,点P是等边
三角形ABC内部一点,连接AP、BP、CP,
且AP2=BP2十CP2,现将△APC绕点A
顺时针旋转到△ADB的位置,对于下列结
论:①△ADP是等边三角形;②△ABP≌
△CBP;
③∠DBP=90°;④∠BDA十
∠BPA=210°.其中正确的结论有
(C)
A.1个
B.2个
C.3个
D.4个
同课章节目录
