第23章 旋转 专题训练(七) 旋转模型构造 习题课件
文档属性
| 名称 | 第23章 旋转 专题训练(七) 旋转模型构造 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
专题训练(七) 旋转模型构造
第二十三章 旋转
必
●
类型1
半角模型
1.已知,如图1,四边形ABCD是正方形,E,F
分别在边BC、CD上,且∠EAF=45°,我
们把这种模型称为“半角模型”,在解决“半
角模型”问题时,旋转是一种常用的方法.
(1)在图1中,连接EF,为了证明结论
“EF=BE十DF”,小亮将△ADF绕点
A顺时针旋转90°后解答了这个问题,
请按小亮的思路写出证明过程;
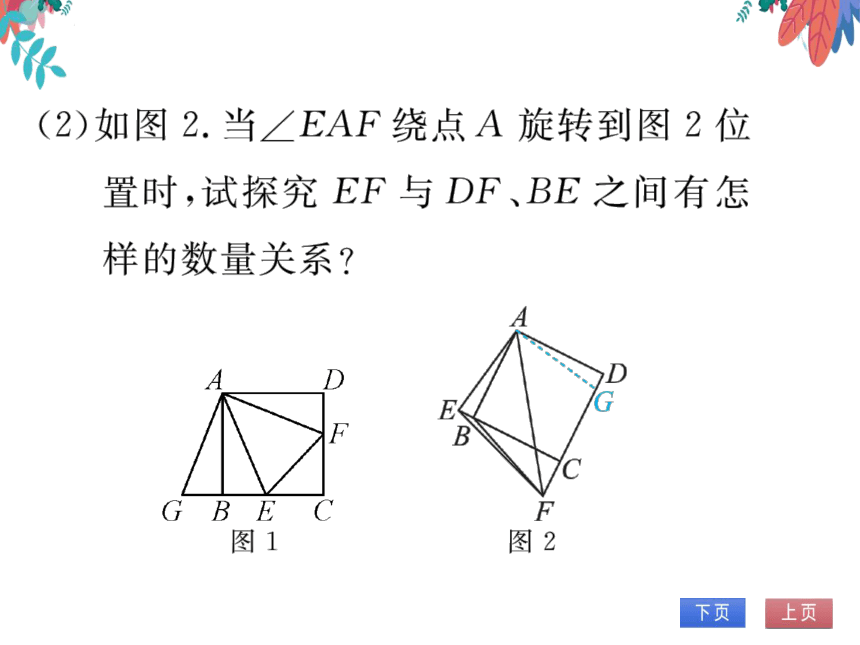
(2)如图2.当∠EAF绕点A旋转到图2位
置时,试探究EF与DF、BE之间有怎
样的数量关系?
B
G
B E
C
F
图1
图2
类型2对角互补模型
2.已知如图,点P是∠MON角平分线上的一
点,∠APB分别交直线OM,OV于点A,
B,∠APB=120°,∠MON=60°.
(1)求证:PA=PB;
(2)若OA=3,OB=6,求OP的值;
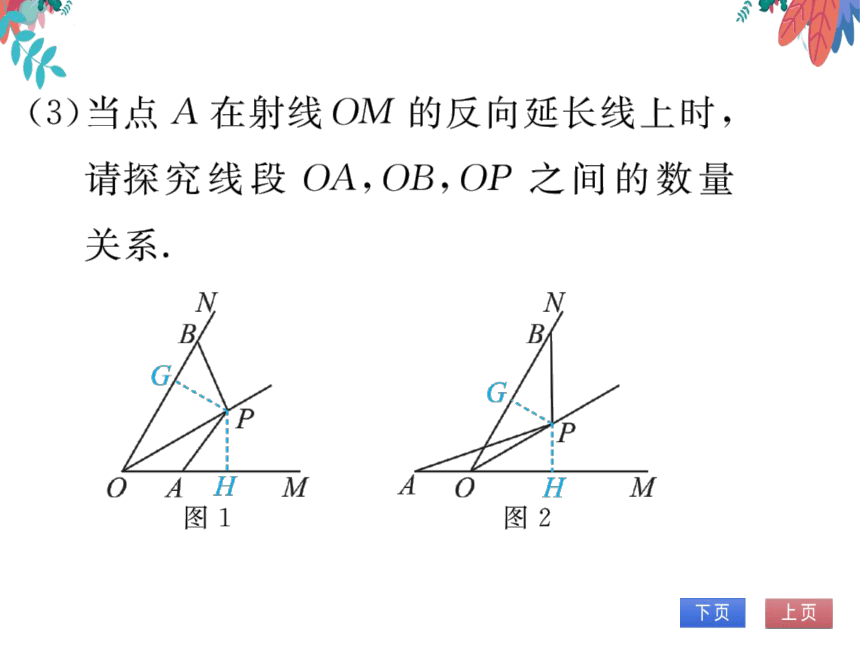
(3)当点A在射线OM的反向延长线上时,
请探究线段OA,OB,OP之间的数量
关系.
N
B
B
G
G
A H M
H
M
图1
图2
解:(1)证明:如图1,过P作PGOB于G,PHOM于H,
.OP平分∠MON,'.OG=OH,.∠MON=60°,∠OGP=
∠OHP=90°,.∠GPH=∠APB=120°,.∠BPG=
∠APH..∠PGB=∠AHP...△BGP≌△AHP(ASA),
。PA=PB;
②当A在点O的左侧时,如图2,过P作PG⊥ON于G.PH
OM于H.设AH=x,同理得:人APH2△BPG,
.AH=BG=x,'.OH=OG=x一3,.OB=6,即2x一3=
6,X=-
,0=}-3=3,R人0P中,0=3,绿
上,OP的长为33或/3.
(3)解:如图2,Rt△0Gp中,:∠G0P=30,.GP=20P,
0G=/POGop,
.0B=0G+BG=0G+AH=20G+O1=0M+2X30p
=OA十/3OP.
类型3中点旋转模型
3.在正方形ABCD的边AB上任取一点E,
作EF⊥AB交BD于点F,取FD的中点
G,连接EG、CG.
(1)试猜想EG与CG之间的关系?请直接
写出你的猜想;
解:(1)EG=CG,且EG⊥CG.证明:过GH⊥AD于点H,延
长HG交CD于点I,作GK⊥AD于点K.则四边形GIDK
是正方形,四边形AKGH是矩形,.AK=HG,KD=DI=
GI=AH,
.AD=CD,.IC=HG,,AD∥GH∥CF,G是DF的中点
'.HA=HE,.'.HE=GI,..Rt△HGE≌Rt△ICG(SAS),
..∠HGE=∠GCI,∠HEG=∠CGI,
EG=CG,..∠HGE十∠CGI=90°,,。∠EGC=90°,.EG
⊥CG;
专题训练(七) 旋转模型构造
第二十三章 旋转
必
●
类型1
半角模型
1.已知,如图1,四边形ABCD是正方形,E,F
分别在边BC、CD上,且∠EAF=45°,我
们把这种模型称为“半角模型”,在解决“半
角模型”问题时,旋转是一种常用的方法.
(1)在图1中,连接EF,为了证明结论
“EF=BE十DF”,小亮将△ADF绕点
A顺时针旋转90°后解答了这个问题,
请按小亮的思路写出证明过程;
(2)如图2.当∠EAF绕点A旋转到图2位
置时,试探究EF与DF、BE之间有怎
样的数量关系?
B
G
B E
C
F
图1
图2
类型2对角互补模型
2.已知如图,点P是∠MON角平分线上的一
点,∠APB分别交直线OM,OV于点A,
B,∠APB=120°,∠MON=60°.
(1)求证:PA=PB;
(2)若OA=3,OB=6,求OP的值;
(3)当点A在射线OM的反向延长线上时,
请探究线段OA,OB,OP之间的数量
关系.
N
B
B
G
G
A H M
H
M
图1
图2
解:(1)证明:如图1,过P作PGOB于G,PHOM于H,
.OP平分∠MON,'.OG=OH,.∠MON=60°,∠OGP=
∠OHP=90°,.∠GPH=∠APB=120°,.∠BPG=
∠APH..∠PGB=∠AHP...△BGP≌△AHP(ASA),
。PA=PB;
②当A在点O的左侧时,如图2,过P作PG⊥ON于G.PH
OM于H.设AH=x,同理得:人APH2△BPG,
.AH=BG=x,'.OH=OG=x一3,.OB=6,即2x一3=
6,X=-
,0=}-3=3,R人0P中,0=3,绿
上,OP的长为33或/3.
(3)解:如图2,Rt△0Gp中,:∠G0P=30,.GP=20P,
0G=/POGop,
.0B=0G+BG=0G+AH=20G+O1=0M+2X30p
=OA十/3OP.
类型3中点旋转模型
3.在正方形ABCD的边AB上任取一点E,
作EF⊥AB交BD于点F,取FD的中点
G,连接EG、CG.
(1)试猜想EG与CG之间的关系?请直接
写出你的猜想;
解:(1)EG=CG,且EG⊥CG.证明:过GH⊥AD于点H,延
长HG交CD于点I,作GK⊥AD于点K.则四边形GIDK
是正方形,四边形AKGH是矩形,.AK=HG,KD=DI=
GI=AH,
.AD=CD,.IC=HG,,AD∥GH∥CF,G是DF的中点
'.HA=HE,.'.HE=GI,..Rt△HGE≌Rt△ICG(SAS),
..∠HGE=∠GCI,∠HEG=∠CGI,
EG=CG,..∠HGE十∠CGI=90°,,。∠EGC=90°,.EG
⊥CG;
同课章节目录
