21.3 实际问题与一元二次方程 第2课时 几何图形面积问题与利润问题 习题课件
文档属性
| 名称 | 21.3 实际问题与一元二次方程 第2课时 几何图形面积问题与利润问题 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:36:59 | ||
图片预览







文档简介
(共22张PPT)
21.3 实际问题与一元二次方程
第2课时 几何图形面积问题与
利润问题
第二十一章 一元二次方程
必
●
知识要点全练
夯实基础
知识点1
几何图形面积问题
1.(兰州中考)公园有一块正方形空地,后来
从这块空地上划出部分区域栽种鲜花(如
图),原空地一边减少了1m,另一边减少了
2m,剩余空地的面积为18m,求原正方形
空地的边长,设原正方形空地的边长为
xm,则可列方程为
(C)
A.(x+1)(x+2)=18B.x2-3x+16=0
C.(x-1)(x-2)=18D.x2+3x+16=0
(第1题图)
2.(2022·温州期中)有一张长方形桌子的桌
面长100cm,宽60cm.有一块长方形台布
的面积是桌面面积的2倍,并且铺在桌面
上时,各边垂下的长度相等.设垂下的长度
为x(cm),根据题意可列方程为
(100+2x)(60+2x)=2X100X60
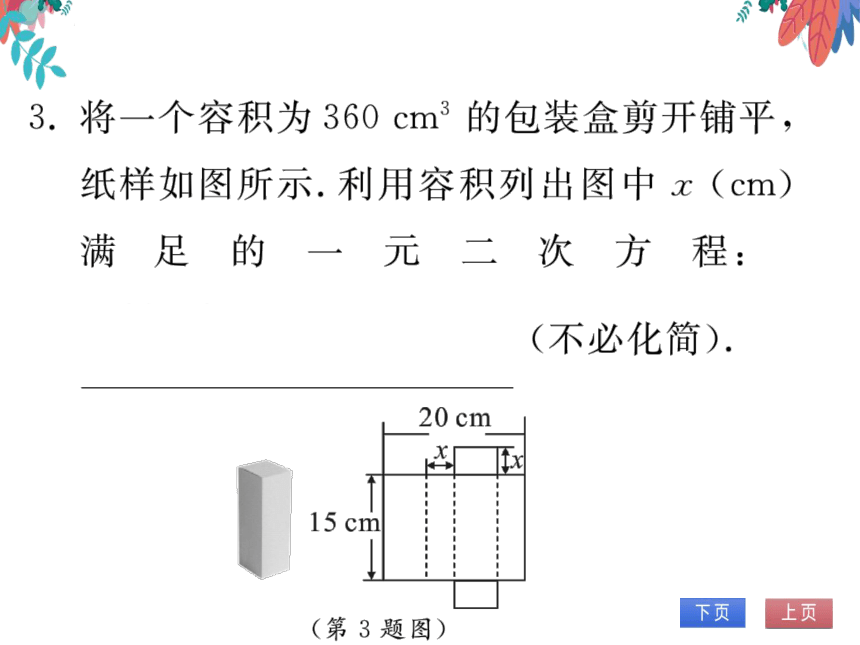
3.将一个容积为360cm3的包装盒剪开铺平,
纸样如图所示.利用容积列出图中x(cm)
满足的
元
二
次方程:
20-2x
。x·15=360
(不必化简).
2
20 cm
x
1
·
0
1
15 cm
I
I
I
1
1
·
1
·
1
·
1
(第3题图)
4.(湖北襄阳中芳)改善小区环境,争创文明家
园.如图,某社区决定在一块长(AD)16m,宽
(AB)9m的矩形场地ABCD上修建三条同样
宽的小路,其中两条与AB平行,另外一条与
AD平行,其余部分种草,要使草坪部分的总
面积是112m,则小路的宽是多少米?
解得x1=1,x2=16(不合题意,舍A
D
去).
答:小路的宽是1m.
B
C
知识点2
利润问题
5.(2022·百色期中)将进价为90元/个的某
种商品按100元/个出售时,能卖出500个,
已知这种商品每个每涨价1元,其销售数
量就减少10个,若想使利润达到9000元,
售价应是多少?设售价为元/个,则可列方
程
(
A.(x-100)(500-10x)=9000
B.(x-90)(500-10x)=9000
C.(x-100)[500-10(x-100)]=9000
D.(x-90)[500-10(x-100)]=9000
6.(2022·乳山市期末)某商场将进价为30元
的台灯以单价40元售出,平均每月能售出
600个.调查表明:这种台灯的单价每上涨
1元,其销售量将减少10个.为实现平均每月
10000元的销售利润,从消费者的角度芳虑,
商场对这种台灯的售价应定为
50
元.
21.3 实际问题与一元二次方程
第2课时 几何图形面积问题与
利润问题
第二十一章 一元二次方程
必
●
知识要点全练
夯实基础
知识点1
几何图形面积问题
1.(兰州中考)公园有一块正方形空地,后来
从这块空地上划出部分区域栽种鲜花(如
图),原空地一边减少了1m,另一边减少了
2m,剩余空地的面积为18m,求原正方形
空地的边长,设原正方形空地的边长为
xm,则可列方程为
(C)
A.(x+1)(x+2)=18B.x2-3x+16=0
C.(x-1)(x-2)=18D.x2+3x+16=0
(第1题图)
2.(2022·温州期中)有一张长方形桌子的桌
面长100cm,宽60cm.有一块长方形台布
的面积是桌面面积的2倍,并且铺在桌面
上时,各边垂下的长度相等.设垂下的长度
为x(cm),根据题意可列方程为
(100+2x)(60+2x)=2X100X60
3.将一个容积为360cm3的包装盒剪开铺平,
纸样如图所示.利用容积列出图中x(cm)
满足的
元
二
次方程:
20-2x
。x·15=360
(不必化简).
2
20 cm
x
1
·
0
1
15 cm
I
I
I
1
1
·
1
·
1
·
1
(第3题图)
4.(湖北襄阳中芳)改善小区环境,争创文明家
园.如图,某社区决定在一块长(AD)16m,宽
(AB)9m的矩形场地ABCD上修建三条同样
宽的小路,其中两条与AB平行,另外一条与
AD平行,其余部分种草,要使草坪部分的总
面积是112m,则小路的宽是多少米?
解得x1=1,x2=16(不合题意,舍A
D
去).
答:小路的宽是1m.
B
C
知识点2
利润问题
5.(2022·百色期中)将进价为90元/个的某
种商品按100元/个出售时,能卖出500个,
已知这种商品每个每涨价1元,其销售数
量就减少10个,若想使利润达到9000元,
售价应是多少?设售价为元/个,则可列方
程
(
A.(x-100)(500-10x)=9000
B.(x-90)(500-10x)=9000
C.(x-100)[500-10(x-100)]=9000
D.(x-90)[500-10(x-100)]=9000
6.(2022·乳山市期末)某商场将进价为30元
的台灯以单价40元售出,平均每月能售出
600个.调查表明:这种台灯的单价每上涨
1元,其销售量将减少10个.为实现平均每月
10000元的销售利润,从消费者的角度芳虑,
商场对这种台灯的售价应定为
50
元.
同课章节目录
