第24章 圆 专题训练(八) 圆的有关性质的应用 习题课件
文档属性
| 名称 | 第24章 圆 专题训练(八) 圆的有关性质的应用 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 14:36:59 | ||
图片预览








文档简介
(共20张PPT)
专题训练(八) 圆的有关性质的应用
第二十四章 圆
必
●
类型1利用同圆的半径(或直径)相等进行
计算或证明
1.
如图,⊙O的直径AB与弦CD的延长线交
于点E,若DE=OB,∠AOC=84°,则∠E
的度数为
(B)
A.42°
B.28°
C.219
D.
209
3.如图,OA,OB是⊙O的半径,C,D分别为
OA,OB的中点.求证:AD=BC.
证明:.OA,OB是⊙O的半径,
。°.OA=OB.
。C,D分别是OA,OB的中点,
B
.0c=201,0D=0B.
2)
.OC=OD,又.·∠AOD=∠BOC,
.'.∠OAD≌△OBC(SAS).
。°。AD=BC
类型2
利用垂径定理进行计算或证明
4.(2022·湖北荆门)如图,CD是圆O的弦,
直径AB⊥CD,垂足为E,若AB=12,
BE=3,则四边形ACBD的面积为
(A)
A.36√/3
B.24√/3
C.18√/3
D.72/3
A
B
D
(第4题图)
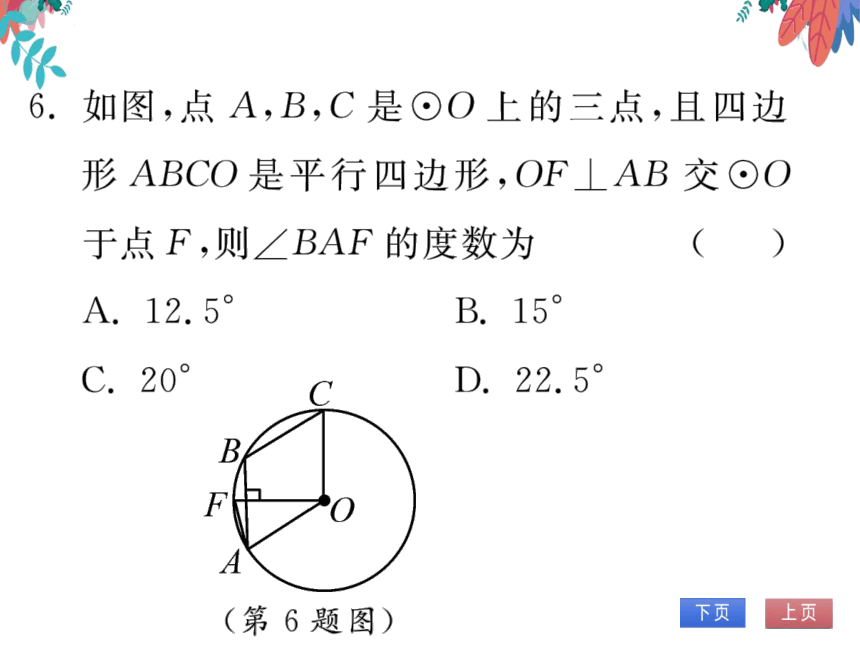
6.如图,点A,B,C是⊙O上的三点,且四边
形ABCO是平行四边形,OF⊥AB交⊙O
于点F,则∠BAF的度数为
(B)
A.12.59
B.15°
C.20°
D.22,5
C
B
F
A
(第6题图)
7.(2022·安徽)已知⊙O的半径为7,AB是
⊙O的弦,点P在弦AB上.若PA=4,
PB=6,则OP等于
(D)
A./14
B.4
C.√/23
D.5
8.如图,在平面直角坐标系中,点A的坐标是
(20,0),点B的坐标是(16,0),点C,D在以
OA为直径的半圆M上,且四边形OCDB是
平行四边形,则点C的坐标为
(2,6)
C
D
0
M
B A
X
(第8题图)
9.在半径为1的圆中,弦AB的长为√/2,弦AC
的长为W/3,则∠BAC=
75或15
10.如图,直线l经过圆心O,交⊙O于A,B
两点,弦CD所在直线交直线于点P,
PA=2,PB=14,∠DPB=30°,则CD的
长为4√/5
B
类型3利用圆周角定理及其推论进行计算
或证明
11.(2022·襄阳月考)如图,点A,B,C,D都在
半径为2的⊙O上,若OABC,∠CDA=30°,
则弦BC的长为
(D)
A.4
B.2√/2
C.
D.2√/3
A
B
C
D
(第11题图)
12.如图,AB是半圆,O为AB的中点,C,D两
点在AB上,且AD∥OC,连接BC,BD.若
CD=62°,则AD的度数为
(A)
A.56°
B.58
C.62°
D.66
专题训练(八) 圆的有关性质的应用
第二十四章 圆
必
●
类型1利用同圆的半径(或直径)相等进行
计算或证明
1.
如图,⊙O的直径AB与弦CD的延长线交
于点E,若DE=OB,∠AOC=84°,则∠E
的度数为
(B)
A.42°
B.28°
C.219
D.
209
3.如图,OA,OB是⊙O的半径,C,D分别为
OA,OB的中点.求证:AD=BC.
证明:.OA,OB是⊙O的半径,
。°.OA=OB.
。C,D分别是OA,OB的中点,
B
.0c=201,0D=0B.
2)
.OC=OD,又.·∠AOD=∠BOC,
.'.∠OAD≌△OBC(SAS).
。°。AD=BC
类型2
利用垂径定理进行计算或证明
4.(2022·湖北荆门)如图,CD是圆O的弦,
直径AB⊥CD,垂足为E,若AB=12,
BE=3,则四边形ACBD的面积为
(A)
A.36√/3
B.24√/3
C.18√/3
D.72/3
A
B
D
(第4题图)
6.如图,点A,B,C是⊙O上的三点,且四边
形ABCO是平行四边形,OF⊥AB交⊙O
于点F,则∠BAF的度数为
(B)
A.12.59
B.15°
C.20°
D.22,5
C
B
F
A
(第6题图)
7.(2022·安徽)已知⊙O的半径为7,AB是
⊙O的弦,点P在弦AB上.若PA=4,
PB=6,则OP等于
(D)
A./14
B.4
C.√/23
D.5
8.如图,在平面直角坐标系中,点A的坐标是
(20,0),点B的坐标是(16,0),点C,D在以
OA为直径的半圆M上,且四边形OCDB是
平行四边形,则点C的坐标为
(2,6)
C
D
0
M
B A
X
(第8题图)
9.在半径为1的圆中,弦AB的长为√/2,弦AC
的长为W/3,则∠BAC=
75或15
10.如图,直线l经过圆心O,交⊙O于A,B
两点,弦CD所在直线交直线于点P,
PA=2,PB=14,∠DPB=30°,则CD的
长为4√/5
B
类型3利用圆周角定理及其推论进行计算
或证明
11.(2022·襄阳月考)如图,点A,B,C,D都在
半径为2的⊙O上,若OABC,∠CDA=30°,
则弦BC的长为
(D)
A.4
B.2√/2
C.
D.2√/3
A
B
C
D
(第11题图)
12.如图,AB是半圆,O为AB的中点,C,D两
点在AB上,且AD∥OC,连接BC,BD.若
CD=62°,则AD的度数为
(A)
A.56°
B.58
C.62°
D.66
同课章节目录
