第24章 圆 本章重难点突破 习题课件

(共27张PPT)
本章重难点突破
第二十四章　圆
必
●
考点1
圆的相关概念
1.下列命题是真命题的是
(D)
A.等弧就是长度相等的弧
B.劣弧一定比优弧短
C.相等的圆心角所对的弦相等
D.直径是圆中最长的弦
考点2三个定理
定理1垂径定理
2.(2022·四川巴中)如图，AB为⊙O的直
径，弦CD交AB于点E,BC=BD,
∠CDB=30°，AC=2W3,则OE等于(C)
1.
3
B.√3
C.1
D.2
2
A
B
E
D
(第2题图)
3.(2022·黑龙江牡丹江)⊙O的直径CD=10,
AB是⊙O的弦，AB⊥CD,垂足为M,OM:
OC=3:5,则AC的长为
4V5或2W5
定理2弧、弦、圆心角定理
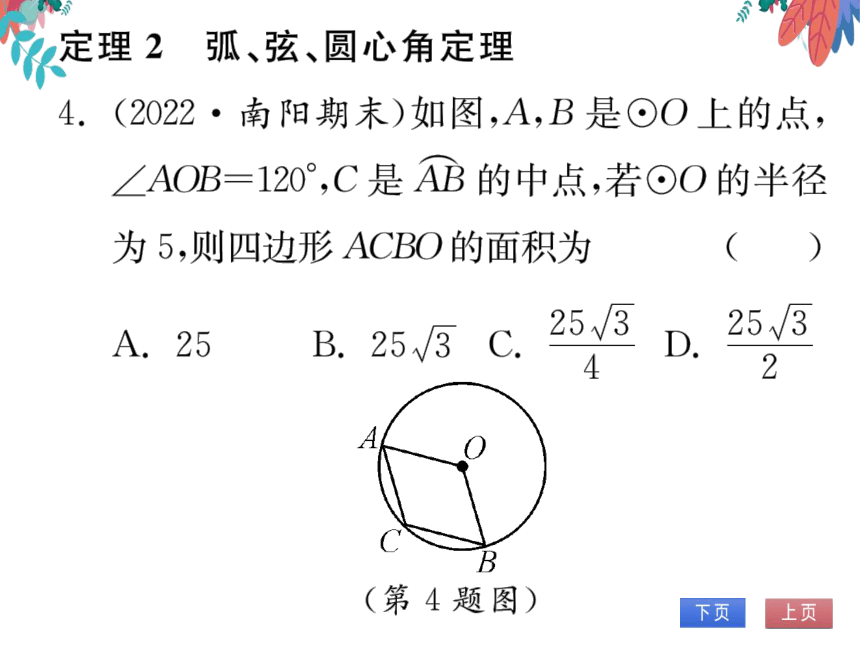
4.(2022·南阳期末)如图，A,B是⊙O上的点，
∠AOB=120°，C是AB的中点，若⊙O的半径
为5，则四边形ACBO的面积为
(D)
B.253C.
25V3
D.
25√3
A.25
4
2
A
C
B
(第4题图)
定理3
圆周角定理
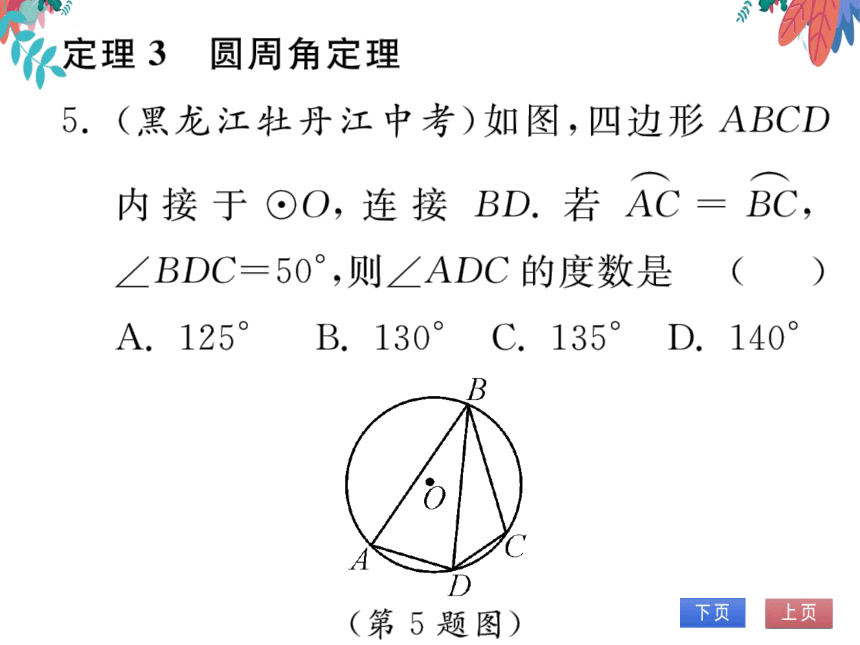
5.(黑龙江牡丹江中考)如图，四边形ABCD
内接于⊙O,连接BD.若AC=BC,
∠BDC=50°，则∠ADC的度数是
B
A.125°
B.130°
C.135°D.140
B
0
A
(第5题图)
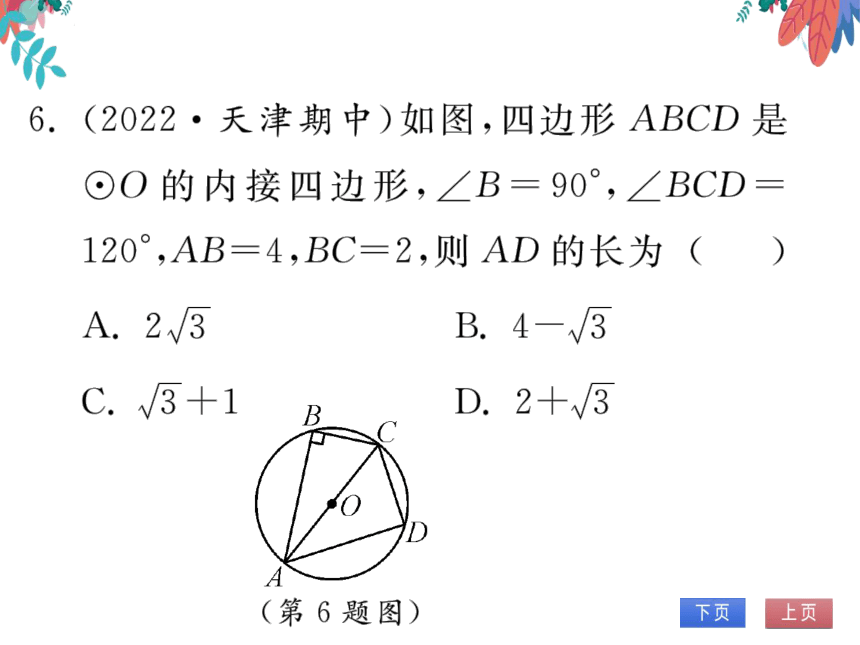
6.(2022·天津期中)如图，四边形ABCD是
⊙O的内接四边形，∠B=90°，∠BCD=
120°，AB=4,BC=2,则AD的长为(D)
A.2/3
B.4-/3
C./3+1
D.2+√/3
B
A
(第6题图)
7.(2022·南京模拟)如图，⊙C经过原点O,
并与两坐标轴相交于A、D两点，已知
∠OBA=60°，点D的坐标是(0,2)，则圆的
半径为
2
B
(第7题图)
8.(四川绵阳中考)如图，AB是⊙O的直径，
点C为BD的中点，CF为⊙O的弦，且
CF⊥AB,垂足为E,连接BD交CF于点
G,连接CD,AD,BF
(1)求证：∧BFG≌∧CDG;
(2)连接AD,若AD=BE=2,求BF的长.
(1)证明：，C是BD的中点，CD=
C
BC.,'AB是⊙O的直径，且CF⊥AD,
G
..BC-BF...CD=BF...CD=BF.
A
B
.△BFG2CDG(AAS).
F
(2)解：连接OF,设⊙O的半径为r.在
Rt△ADB中，BD2=AB2一AD2,即BD2=(2r)2一2，
在Rt△OEF中，OF2=OE2+EF2,即EF2=r2一（r一2)2.
.CD=BC=BF,.'BD=CF..'BD=CF..'BD2=CF2=
(2EF)2=4EF2,即(2r)2一22=4[r2一（r一2)2]，解得r=1
(舍)或r=3,..BF2=EF2十BE=32一（3一2)2+22=12.
..BF=2/3.