物理人教版(2019)必修第二册8.4机械能守恒定律(共30张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.4机械能守恒定律(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 61.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-06-13 17:34:31 | ||
图片预览





文档简介
(共30张PPT)
8.4 机械能守恒定律
人教版(2019)物理(必修第二册)
第八章 机械能守恒定律
课堂导入
生活中有很多动能和势能相互转化的例子
动能和势能之间的转化是通过什么来实现的呢?动能和势能之间的相互转化遵循什么规律呢?
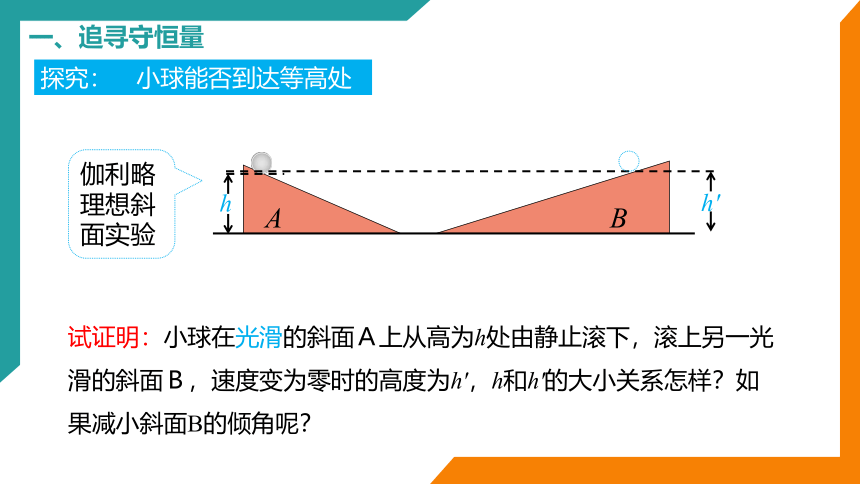
一、追寻守恒量
伽利略理想斜面实验
A
B
h
h'
探究: 小球能否到达等高处
试证明:小球在光滑的斜面A上从高为h处由静止滚下,滚上另一光滑的斜面B,速度变为零时的高度为h',h和h'的大小关系怎样?如果减小斜面B的倾角呢?
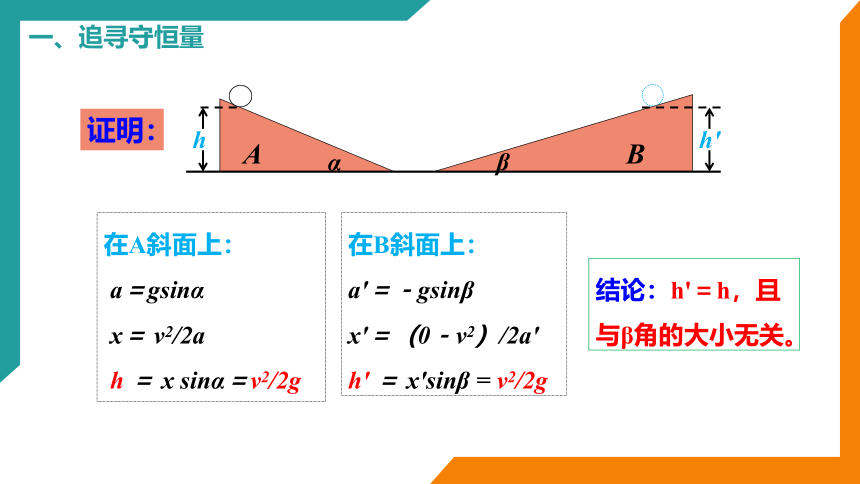
一、追寻守恒量
在A斜面上:
a=gsinα
x= v2/2a
h = x sinα=v2/2g
在B斜面上:
a'=-gsinβ
x'=(0-v2)/2a'
h' = x'sinβ = v2/2g
结论:h'=h,且与β角的大小无关。
A
B
h
h'
α
β
证明:
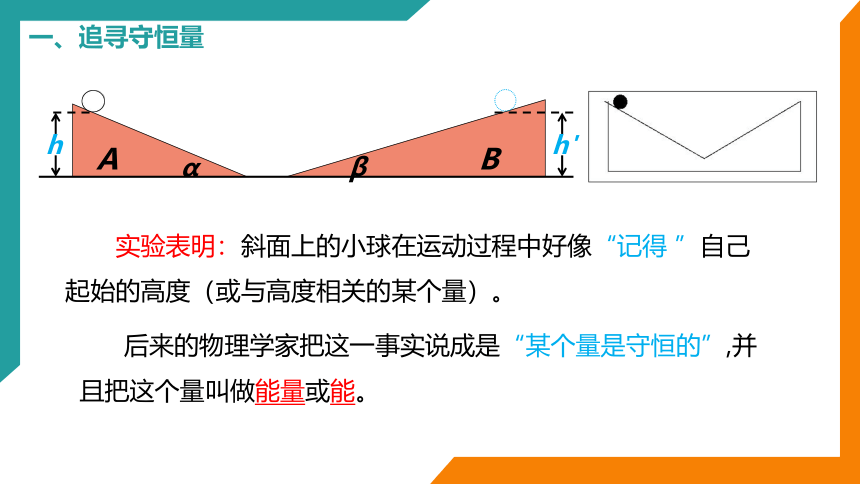
一、追寻守恒量
实验表明:斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
A
B
h
h'
α
β
一、追寻守恒量
碰鼻实验:
如图所示,把悬挂的小球拉至鼻尖由静止释放,实验者立于原地不动,小球来回摆动,小球能否碰到鼻子?为什么?
重力
势能
动能
重力做功
一、追寻守恒量
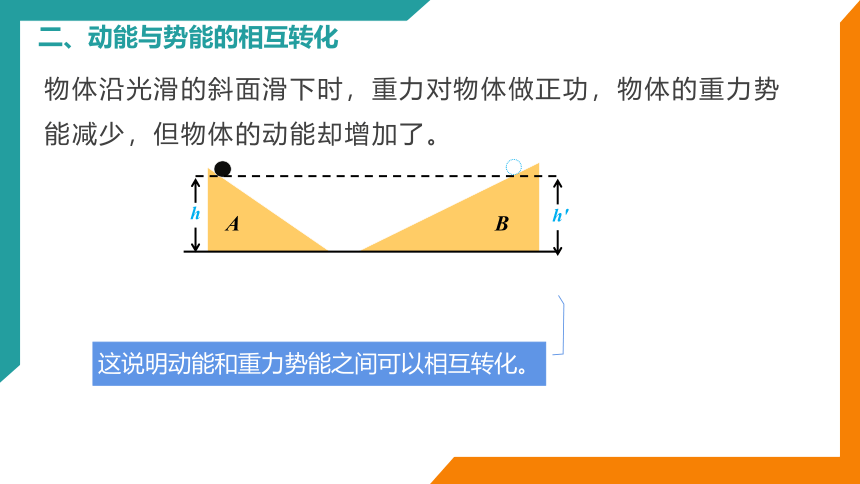
二、动能与势能的相互转化
物体沿光滑的斜面滑下时,重力对物体做正功,物体的重力势能减少,但物体的动能却增加了。
A
B
h
h'
这说明动能和重力势能之间可以相互转化。
二、动能与势能的相互转化
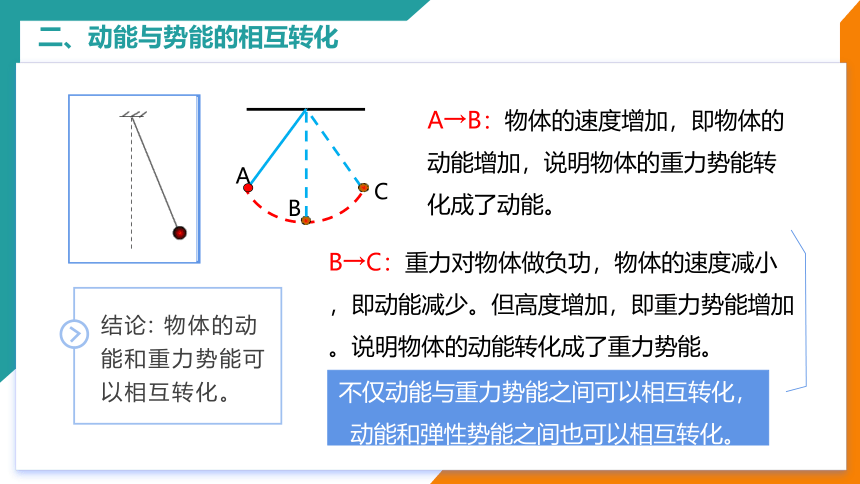
A→B:物体的速度增加,即物体的动能增加,说明物体的重力势能转化成了动能。
A
C
B
B→C:重力对物体做负功,物体的速度减小,即动能减少。但高度增加,即重力势能增加。说明物体的动能转化成了重力势能。
结论: 物体的动能和重力势能可以相互转化。
不仅动能与重力势能之间可以相互转化,动能和弹性势能之间也可以相互转化。
二、动能与势能的相互转化
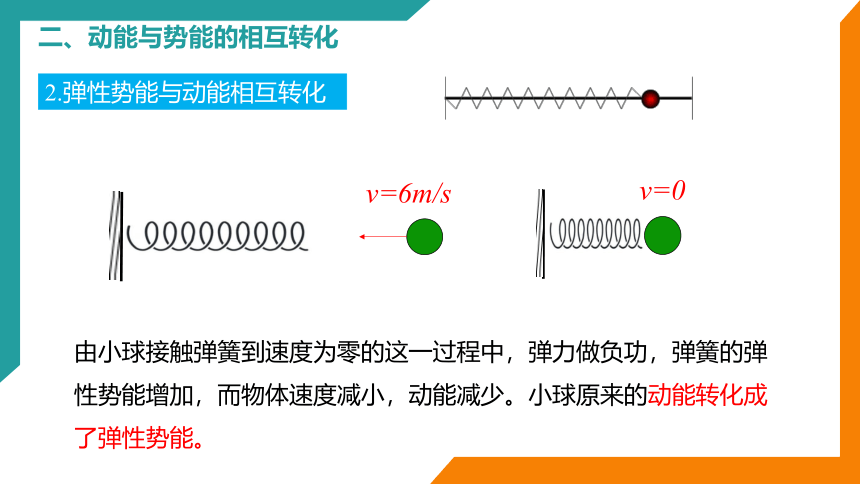
2.弹性势能与动能相互转化
由小球接触弹簧到速度为零的这一过程中,弹力做负功,弹簧的弹性势能增加,而物体速度减小,动能减少。小球原来的动能转化成了弹性势能。
v=6m/s
v=0
二、动能与势能的相互转化
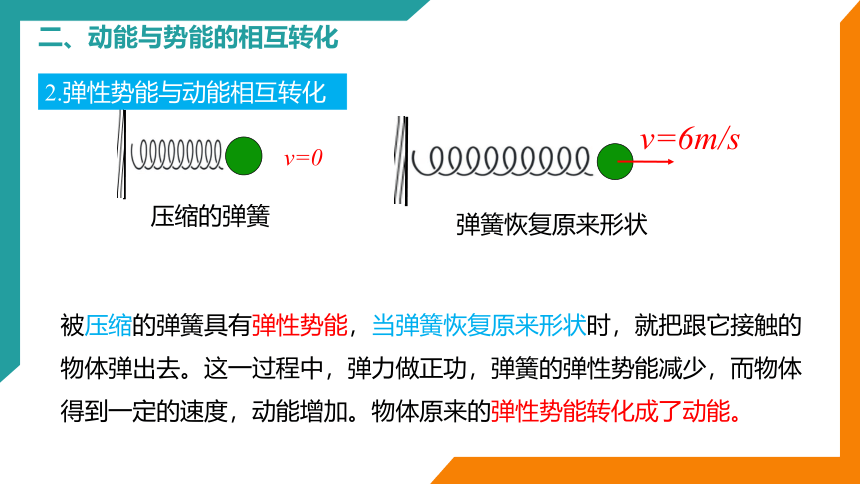
被压缩的弹簧具有弹性势能,当弹簧恢复原来形状时,就把跟它接触的物体弹出去。这一过程中,弹力做正功,弹簧的弹性势能减少,而物体得到一定的速度,动能增加。物体原来的弹性势能转化成了动能。
弹簧恢复原来形状
v=6m/s
压缩的弹簧
v=0
2.弹性势能与动能相互转化
二、动能与势能的相互转化
3.机械能
重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能(mechanical energy)。通过重力或弹力做功,机械能可以从一种形式转化成另一种形式。
(2)机械能是标量,具有相对性
(1)表达式:
二、动能与势能的相互转化
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方。在这两种情况下,重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
想一想
三、机械能守恒定律
如下图中,质量为m的物体均从高为h1的A点运动到高为h2的B点,求这四个过程中重力对物体做的功?(不计空气阻力和摩擦阻力)
若物体在A点的速度为v1,所有阻力均不计,求物体到达B点时的动能Ek2
由动能定理知:
机械能守恒定律推导
由重力做功与重力势能的关系得
三、机械能守恒定律
上述四例中有何共性?
故:
上式表示:动能和重力势能之和即总的机械能保持不变。
1.只有重力做功; 2.动能与势能在相互转化。
移项
即ΔEk= ΔEP
机械能守恒定律推导
三、机械能守恒定律
如果物体沿粗糙面下滑呢?
粗糙曲面滑下
v0
mg
FN
F阻
Ek2+EP2≠Ek1+EP1
即 E1≠E2
结论:除重力外有其他力做功,机械能改变。
想一想
在只有重力做功的物体系统内,动能与重力势能可以互相转化,而总的机
械能保持不变。
三、机械能守恒定律
若地面光滑,根据动能定理
W弹=Ek2-Ek1
W弹=-ΔEp=Ep1-Ep2
由两式得Ek2-Ek1=Ep1-Ep2
Ek2+Ep2=Ek1+Ep1 即E2=E1
Ek2
Ep2
Ek1
Ep1
在只有弹簧弹力做功的物体和弹簧系统内,动能和弹性势能相互转化,且
机械能的总量保持不变。
由弹力做功与弹性势能的变化关系得
在光滑水平面上,设弹簧被压缩x1时弹性势能为EP1,动能为EK1,设弹簧被压缩x2时弹性势能为EP2,能为EK2
三、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
2.表达式:
守恒观点
转化观点
转移观点
或 ΔEk减=ΔEp增
或 ΔEA减=ΔEB增
(3)ΔEA=-ΔEB
(2)ΔEk= -ΔEp
(1)EK2+EP2=EK1+EP1 即 E2=E1
三、机械能守恒定律
3.守恒条件:物体系统内只有重力或弹力做功(其他力不做功),机械能守恒。(此处弹力高中阶段特指弹簧类弹力)
对守恒条件的理解:
系统不受外力。
系统受其他力,而其他力不做功,只有重力(弹力)做功;
系统受外力,除重力(弹力)以外的力也做功,但外力做功的代数和为零。
三、机械能守恒定律
(1)用做功来分析:分析物体或物体系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体或物体系统的机械能守恒。
(2)用能量转化来分析:若物体系统中只有动能和势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒.
(3)用增减情况分析:若物体系统的动能与势能均增加,则系统机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统机械能不守恒。
4、判断机械能是否守恒的方法:
对于由两个或两个以上物体(包括弹簧在内组成的系统),如果系统只有重力做功或弹力做功,物体间只有动能、重力势能和弹性势能之间的相互转化,系统与外界没有机械能的转移,也没有机械能与其他形式能的转化,则系统的机械能就守恒。
拓展
三、机械能守恒定律
课堂小结
课堂练习
1.(机械能守恒的判断)下列物体在运动过程中,可视为机械能守恒的是( )
A.飘落中的树叶
B.乘电梯匀速上升的人
C.被掷出后在空中运动的铅球
D.沿粗糙斜面匀速下滑的木箱
答案:C
解析:A项中,空气阻力对树叶做功,机械能不守恒。B项中人的动能不变,重力势能变化,机械能变化。C项中,空气阻力可以忽略不计,只有重力做功,机械能守恒。D项中,木箱动能不变,重力势能减少,机械能减少。
课堂练习
2.(机械能守恒的判断)如图所示,P、Q两球质量相等,开始两球静止,将P上方的细绳烧断,在Q落地之前,下列说法正确的是(不计空气阻力)( )
A.在任一时刻,两球动能相等
B.在任一时刻,两球加速度相等
C.在任一时刻,系统动能和重力势能之和保持不变
D.在任一时刻,系统机械能是不变的
答案:D
课堂练习
解析:细绳烧断后,由于弹簧处于伸长状态,通过对P、Q两球受力分析可知aP>aQ,在任一时刻,两球的动能不一定相等,选项A、B错误。系统内有弹力做功,弹性势能发生变化,系统的动能和重力势能之和发生变化,选项C错误。Q落地前,两球及弹簧组成的系统只有重力和弹簧的弹力做功,整个系统的机械能守恒,选项D正确。
课堂练习
3.(机械能守恒定律的应用)某同学身高1.8 m,在运动会上他参加跳高比赛,起跳后身体横着越过了1.8 m高度的横杆(如图所示),据此可估算出他起跳时竖直向上的速度大约为(g取10 m/s2)( )
A.2 m/s
B.4 m/s
C.6 m/s
D.8 m/s
答案:B
课堂练习
解析:将该同学视为做竖直上抛运动,整个过程机械能守恒,取地面为参考平面,最高点速度为零,由Ek1+Ep1=Ek2+Ep2得
课堂练习
4.(机械能守恒定律的综合应用)如图
所示,半径R=0.50 m的光滑四分之一
圆弧轨道MN竖直固定在水平桌面上,
轨道末端水平且端点N处于桌面边缘,
把质量m=0.20 kg的小物块从圆弧轨
道上某点由静止释放,经过N点后做平抛运动,到达地面上的P点。已知桌面高度h1=0.80 m,小物块经过N点时的速度v0=3.0 m/s,g取10 m/s2。不计空气阻力,物块可视为质点,求:
(1)圆弧轨道上释放小物块的位置与桌面间的高度差;
(2)小物块经过N点时轨道对物块支持力的大小;
(3)小物块落地前瞬间的速度大小。
课堂练习
解析:(1)设圆弧轨道上释放小物块的位置与桌面间的高度差为h2,小物块运动至N点过程中机械能守恒,则有
解得F=5.6 N。
多谢欣赏!
8.4 机械能守恒定律
人教版(2019)物理(必修第二册)
第八章 机械能守恒定律
课堂导入
生活中有很多动能和势能相互转化的例子
动能和势能之间的转化是通过什么来实现的呢?动能和势能之间的相互转化遵循什么规律呢?
一、追寻守恒量
伽利略理想斜面实验
A
B
h
h'
探究: 小球能否到达等高处
试证明:小球在光滑的斜面A上从高为h处由静止滚下,滚上另一光滑的斜面B,速度变为零时的高度为h',h和h'的大小关系怎样?如果减小斜面B的倾角呢?
一、追寻守恒量
在A斜面上:
a=gsinα
x= v2/2a
h = x sinα=v2/2g
在B斜面上:
a'=-gsinβ
x'=(0-v2)/2a'
h' = x'sinβ = v2/2g
结论:h'=h,且与β角的大小无关。
A
B
h
h'
α
β
证明:
一、追寻守恒量
实验表明:斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
A
B
h
h'
α
β
一、追寻守恒量
碰鼻实验:
如图所示,把悬挂的小球拉至鼻尖由静止释放,实验者立于原地不动,小球来回摆动,小球能否碰到鼻子?为什么?
重力
势能
动能
重力做功
一、追寻守恒量
二、动能与势能的相互转化
物体沿光滑的斜面滑下时,重力对物体做正功,物体的重力势能减少,但物体的动能却增加了。
A
B
h
h'
这说明动能和重力势能之间可以相互转化。
二、动能与势能的相互转化
A→B:物体的速度增加,即物体的动能增加,说明物体的重力势能转化成了动能。
A
C
B
B→C:重力对物体做负功,物体的速度减小,即动能减少。但高度增加,即重力势能增加。说明物体的动能转化成了重力势能。
结论: 物体的动能和重力势能可以相互转化。
不仅动能与重力势能之间可以相互转化,动能和弹性势能之间也可以相互转化。
二、动能与势能的相互转化
2.弹性势能与动能相互转化
由小球接触弹簧到速度为零的这一过程中,弹力做负功,弹簧的弹性势能增加,而物体速度减小,动能减少。小球原来的动能转化成了弹性势能。
v=6m/s
v=0
二、动能与势能的相互转化
被压缩的弹簧具有弹性势能,当弹簧恢复原来形状时,就把跟它接触的物体弹出去。这一过程中,弹力做正功,弹簧的弹性势能减少,而物体得到一定的速度,动能增加。物体原来的弹性势能转化成了动能。
弹簧恢复原来形状
v=6m/s
压缩的弹簧
v=0
2.弹性势能与动能相互转化
二、动能与势能的相互转化
3.机械能
重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能(mechanical energy)。通过重力或弹力做功,机械能可以从一种形式转化成另一种形式。
(2)机械能是标量,具有相对性
(1)表达式:
二、动能与势能的相互转化
一个小球在真空中做自由落体运动,另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为 h1 的地方下落到高度为 h2 的地方。在这两种情况下,重力做的功相等吗?重力势能的变化相等吗?动能的变化相等吗?重力势能各转化成什么形式的能?
想一想
三、机械能守恒定律
如下图中,质量为m的物体均从高为h1的A点运动到高为h2的B点,求这四个过程中重力对物体做的功?(不计空气阻力和摩擦阻力)
若物体在A点的速度为v1,所有阻力均不计,求物体到达B点时的动能Ek2
由动能定理知:
机械能守恒定律推导
由重力做功与重力势能的关系得
三、机械能守恒定律
上述四例中有何共性?
故:
上式表示:动能和重力势能之和即总的机械能保持不变。
1.只有重力做功; 2.动能与势能在相互转化。
移项
即ΔEk= ΔEP
机械能守恒定律推导
三、机械能守恒定律
如果物体沿粗糙面下滑呢?
粗糙曲面滑下
v0
mg
FN
F阻
Ek2+EP2≠Ek1+EP1
即 E1≠E2
结论:除重力外有其他力做功,机械能改变。
想一想
在只有重力做功的物体系统内,动能与重力势能可以互相转化,而总的机
械能保持不变。
三、机械能守恒定律
若地面光滑,根据动能定理
W弹=Ek2-Ek1
W弹=-ΔEp=Ep1-Ep2
由两式得Ek2-Ek1=Ep1-Ep2
Ek2+Ep2=Ek1+Ep1 即E2=E1
Ek2
Ep2
Ek1
Ep1
在只有弹簧弹力做功的物体和弹簧系统内,动能和弹性势能相互转化,且
机械能的总量保持不变。
由弹力做功与弹性势能的变化关系得
在光滑水平面上,设弹簧被压缩x1时弹性势能为EP1,动能为EK1,设弹簧被压缩x2时弹性势能为EP2,能为EK2
三、机械能守恒定律
1.内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
2.表达式:
守恒观点
转化观点
转移观点
或 ΔEk减=ΔEp增
或 ΔEA减=ΔEB增
(3)ΔEA=-ΔEB
(2)ΔEk= -ΔEp
(1)EK2+EP2=EK1+EP1 即 E2=E1
三、机械能守恒定律
3.守恒条件:物体系统内只有重力或弹力做功(其他力不做功),机械能守恒。(此处弹力高中阶段特指弹簧类弹力)
对守恒条件的理解:
系统不受外力。
系统受其他力,而其他力不做功,只有重力(弹力)做功;
系统受外力,除重力(弹力)以外的力也做功,但外力做功的代数和为零。
三、机械能守恒定律
(1)用做功来分析:分析物体或物体系统的受力情况(包括内力和外力),明确各力做功的情况,若对物体或系统只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体或物体系统的机械能守恒。
(2)用能量转化来分析:若物体系统中只有动能和势能的相互转化,系统跟外界没有发生机械能的传递,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒.
(3)用增减情况分析:若物体系统的动能与势能均增加,则系统机械能不守恒;若系统的动能不变,而势能发生了变化,或系统的势能不变,而动能发生了变化,则系统机械能不守恒。
4、判断机械能是否守恒的方法:
对于由两个或两个以上物体(包括弹簧在内组成的系统),如果系统只有重力做功或弹力做功,物体间只有动能、重力势能和弹性势能之间的相互转化,系统与外界没有机械能的转移,也没有机械能与其他形式能的转化,则系统的机械能就守恒。
拓展
三、机械能守恒定律
课堂小结
课堂练习
1.(机械能守恒的判断)下列物体在运动过程中,可视为机械能守恒的是( )
A.飘落中的树叶
B.乘电梯匀速上升的人
C.被掷出后在空中运动的铅球
D.沿粗糙斜面匀速下滑的木箱
答案:C
解析:A项中,空气阻力对树叶做功,机械能不守恒。B项中人的动能不变,重力势能变化,机械能变化。C项中,空气阻力可以忽略不计,只有重力做功,机械能守恒。D项中,木箱动能不变,重力势能减少,机械能减少。
课堂练习
2.(机械能守恒的判断)如图所示,P、Q两球质量相等,开始两球静止,将P上方的细绳烧断,在Q落地之前,下列说法正确的是(不计空气阻力)( )
A.在任一时刻,两球动能相等
B.在任一时刻,两球加速度相等
C.在任一时刻,系统动能和重力势能之和保持不变
D.在任一时刻,系统机械能是不变的
答案:D
课堂练习
解析:细绳烧断后,由于弹簧处于伸长状态,通过对P、Q两球受力分析可知aP>aQ,在任一时刻,两球的动能不一定相等,选项A、B错误。系统内有弹力做功,弹性势能发生变化,系统的动能和重力势能之和发生变化,选项C错误。Q落地前,两球及弹簧组成的系统只有重力和弹簧的弹力做功,整个系统的机械能守恒,选项D正确。
课堂练习
3.(机械能守恒定律的应用)某同学身高1.8 m,在运动会上他参加跳高比赛,起跳后身体横着越过了1.8 m高度的横杆(如图所示),据此可估算出他起跳时竖直向上的速度大约为(g取10 m/s2)( )
A.2 m/s
B.4 m/s
C.6 m/s
D.8 m/s
答案:B
课堂练习
解析:将该同学视为做竖直上抛运动,整个过程机械能守恒,取地面为参考平面,最高点速度为零,由Ek1+Ep1=Ek2+Ep2得
课堂练习
4.(机械能守恒定律的综合应用)如图
所示,半径R=0.50 m的光滑四分之一
圆弧轨道MN竖直固定在水平桌面上,
轨道末端水平且端点N处于桌面边缘,
把质量m=0.20 kg的小物块从圆弧轨
道上某点由静止释放,经过N点后做平抛运动,到达地面上的P点。已知桌面高度h1=0.80 m,小物块经过N点时的速度v0=3.0 m/s,g取10 m/s2。不计空气阻力,物块可视为质点,求:
(1)圆弧轨道上释放小物块的位置与桌面间的高度差;
(2)小物块经过N点时轨道对物块支持力的大小;
(3)小物块落地前瞬间的速度大小。
课堂练习
解析:(1)设圆弧轨道上释放小物块的位置与桌面间的高度差为h2,小物块运动至N点过程中机械能守恒,则有
解得F=5.6 N。
多谢欣赏!
