山东省菏泽市定陶区山大附中实验学校 2022-2023学年高一下学期6月月考-数学(含答案)
文档属性
| 名称 | 山东省菏泽市定陶区山大附中实验学校 2022-2023学年高一下学期6月月考-数学(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1007.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 00:00:00 | ||
图片预览




文档简介
高一第二学期第三次阶段性测试
数学试题
一、单项选择题:本大题共8小题.每小题5分,共40分.
1.复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知平面向量,,与垂直,则的值是( )
A. B.1 C. D.2
3.若一个圆锥的底面面积为,其侧面展开图是圆心角为的扇形,则该圆锥的体积为( )
A. B. C. D.
4.若m,n,为三条不同的直线,,为两个不重合的平面,则下列命题正确的是( )
A.如果,,则 B.如果,,m||,n||,则
C.如果,,则 D.如果,,,则
5.一个人连续射击次,则下列各事件关系中,说法正确的是( )
A.事件“两次均击中”与事件“至少一次击中”互为对立事件
B.事件“第一次击中”与事件“第二次击中”为互斥事件
C.事件“两次均未击中”与事件“至多一次击中”互为对立事件
D.事件“恰有一次击中”与事件“两次均击中”为互斥事件
6.某校为了解学生每个月在图书馆借阅书籍的数量,图书管理员甲抽取了一个容量为100的样本,并算得样本的平均数为5,方差为9;图书管理员乙也抽取了一个容量为100的样本,并算得样本的平均数为7,方差为16.若将这两个样本合在一起组成一个容量为200的新样本,则新样本数据的( )
A.平均数为6 B.平均数为6.5 C.方差为12.5 D.方差为13
7.如图,AB是底部B不可到达的一座建筑物,
A为建筑物的最高点,为了测量建筑物高度AB,我们选择一条水平基线HG,使H,G,B三点在同一直线上,经测量,在G,H两点用测角仪器测得A的仰角分别是,,米,测角仪器的高是1.5米,则该建筑物的高AB约为( )(参考数据:)
A.13.5米 B.14.2米 C.15.2米 D.16.5米
8.在三棱锥中,平面平面BCD,是以CD为斜边的等腰直角三角形,M为CD中点,,,则该三棱锥的外接球的表面积为( )
A. B. C. D.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.下列说法正确的是( )
A.向量在向量上的投影向量可表示为
B.若,则与的夹角θ的范围是
C.若,,则
D.已知,,则
10.近年,随着人工智能,AIoT,云计算等技术的推动,全球数据量正在无限制地扩展和增加.国际数据公司IDC统计了2016~2020年全球每年产生的数据量及其增速,所得结果如图所示,根据该统计图,下列说法正确的是( )
A.2016~2020年,全球每年产生的数据量在持续增加
B.2016~2020年,全球数据量的年平均增长率持续下降
C.2016~2020年,全球每年产生的数据量的平均数为33.7
D.2015年,全球产生的数据量超过15
11.已知a,b,c分别是三个内角A,B,C的对边,则下列命题中正确的是( )
A.若,则
B.若是边长为1的正三角形,则
C.若,,,则有一解
D.若是所在平面内的一点,且,则是直角三角形
12.正方体中,E是棱的中点,F在侧面上运动,且满足平面.以下命题正确的有( )
A.侧面上存在点F,使得
B.直线与直线所成角可能为
C.平面与平面所成锐二面角的正切值为
D.设正方体棱长为1,则过点E,F,A的平面截正方体所得的截面面积最大为
三、填空题:本大题共4小题,每小题5分,共20分.
13.已知一组数据8.6,8.9,9.1,9.6,9.7,9.8,9.9,10.2,10.6,10.8,11.2,11.7,则该组数据的第80百分位数为__________.
14.如图,是斜二测画法画出的水平放置的的直观图,是的中点,且轴,轴,,,则的周长______.
15.在中,为中点,若,则实数的值为___________.
16..如图, 二面角的平面角的大小为为半平面内的两个点, 为半平面内一点, 且, 若直线与平面所成角为为的中点, 则线段长度的最大值是___________.
、
四.解答题:本大题共6小题,共70分.
17.(10分).已知某校高一、高二、高三三个年级的学生志愿者人数分别为180,120,120.现采用样本按比例分配的分层随机抽样方法,从中抽取7名同学去敬老院参加献爱心活动.
(1)应从高一、高二、高三三个年级的学生志愿者中分别抽取多少人?
(2)抽出的7名同学分别用A,B,C,D,E,F,G表示,现从该7名同学中随机抽取2名同学承担敬老院卫生打扫工作.设7名同学中来自高一的3人分别为A,B,C,记事件“抽取的两名同学中至少有一名来自高一年级”,试用所给字母写出事件M包含的样本点;
18(12分).的内角的对边分别为,,且______.
在①,②,这两个条件中任选一个,补充在横线中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)求的面积;
(2)若,求.
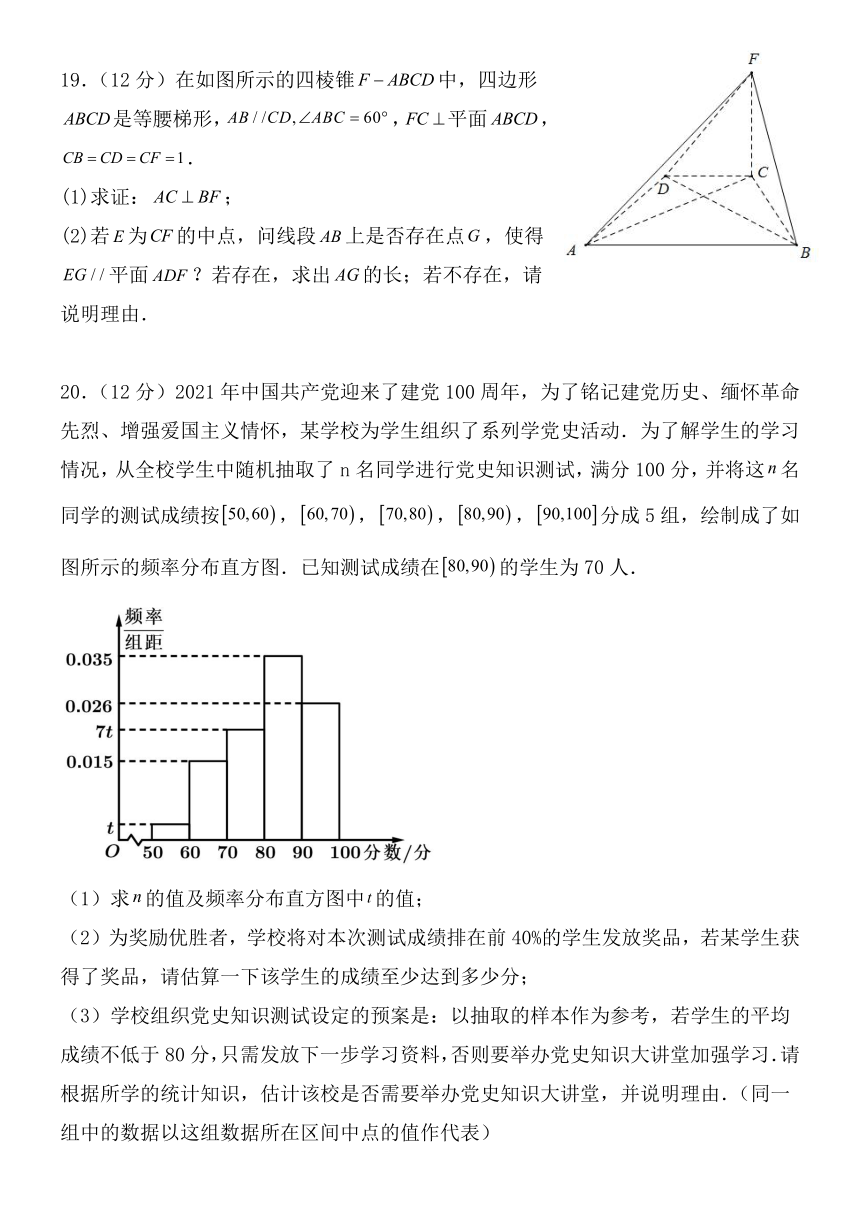
19.(12分)在如图所示的四棱锥中,四边形是等腰梯形,,平面,.
(1)求证:;
(2)若为的中点,问线段上是否存在点,使得平面?若存在,求出的长;若不存在,请说明理由.
20.(12分)2021年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某学校为学生组织了系列学党史活动.为了解学生的学习情况,从全校学生中随机抽取了n名同学进行党史知识测试,满分100分,并将这名同学的测试成绩按,,,,分成5组,绘制成了如图所示的频率分布直方图.已知测试成绩在的学生为70人.
(1)求的值及频率分布直方图中的值;
(2)为奖励优胜者,学校将对本次测试成绩排在前40%的学生发放奖品,若某学生获得了奖品,请估算一下该学生的成绩至少达到多少分;
(3)学校组织党史知识测试设定的预案是:以抽取的样本作为参考,若学生的平均成绩不低于80分,只需发放下一步学习资料,否则要举办党史知识大讲堂加强学习.请根据所学的统计知识,估计该校是否需要举办党史知识大讲堂,并说明理由.(同一组中的数据以这组数据所在区间中点的值作代表)
21.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且.
(1)求角B的大小;
(2)若,D为AC边上的一点,,且__________ ,求△ABC的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
①BD是∠ABC的平分线;②D为线段AC的中点.
(注:如果选择多个条件分别解答,则按第一个解答记分.)
22.(12分)如图,四棱锥的底面是正方形,平面,.点是的中点,作,交于点.
(1)设平面与平面的交线为,试判断直线与直线的位置关系,并给出证明;
(2)求平面与平面所成的较小的二面角的余弦值;
(3)求直线与平面所成角的正切值.
高一第二学期第三次阶段性测试数学试题答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 D A B C D A C D AB ACD AD AC
13.10.8. 14.. 15. 16.
8.【详解】因为是以CD为斜边的等腰直角三角形,M为CD中点,,
所以AM⊥CD,且,
因为,所以,而,
由勾股定理得:,所以BM=BC,
故为等腰直角三角形,,,由题意得:球心O在平面ACD的投影与M点重合,因为平面平面BCD,所以球心O在平面BCD上,在平面BCD上,过点M作MH⊥CD,故,
球心O在MH上,设OM=x,由余弦定理得:,则,
由得:,解得:,设外接球半径为,则,
故该三棱锥的外接球的表面积为.
12.【详解】取中点M,中点N,连接,则易证得,,从而平面平面,所以点F的运动轨迹为线段.
取的中点F,因为是等腰三角形,所以,又因为,所以,故A正确;设正方体的棱长为a,当点F与点M或点N重合时,直线与直线所成角最大,此时,所以B错误;
平面平面,取F为的中点,则,,∴即为平面与平面所成的锐二面角,,所以C正确;
因为当F为与的交点时,截面为菱形(为的中点),面积为,故D错误.
16..【详解】如图,自点引平面的垂线,垂足为,因为,
则A,B两点在以CO为高以CA,CB为母线的圆锥的底面圆周上,所以当A,B
两点运动到公共棱上时AD最大.
自点引公共棱的垂线OH,则,不难解出,在中,由余弦定理得:,
又在中由余弦定理得:
17.解析:(1)由题意知,高一、高二、高三,三个年级的学生志愿者人数之比为,又采用样本量按比例分配的分层随机抽样方法,从中抽取7名同学.
故应从高一、高二、高三,三个年级的学生志愿者中分别抽取3人,2人,2人.
,,,,,,,,,,,,,,,共含有15个样本点.
18.【详解】(1)若选①:因为,由余弦定理得,整理得,则,又,则,,则;
若选②:因为,即,则,又,则,又,得,
则;
(2)由正弦定理得:,,
则,.
19.(1)证明:因为四边形是等腰梯形,,所以,因为,所以,因为,所以所以在中,,即,因为平面,平面,所以,因为,平面,所以平面,因为平面,所以.
(2)解:线段上存在点,使得平面,.下面证明结论:如图,取中点,连接,在线段上取点,使得,连接,由(1)知,在中,,,所以,因为,,所以,因为为中点,为的中点,所以,所以,所以四边形为平行四边形,所以,因为平面,平面,所以平面.所以线段上存在点,使得平面,.
20.【详解】(1)由已知条件可得,由频率和为1得,解得.
(2)因为,所以问题转化为估计样本数据的第60百分位数,
因为,
,所以第60百分位数在区间内,设该生得分最低为,则,
解得,所以估计该生的得分至少达到86分.
(3)由频率分布直方图可得
,因为,
所以按照学校的预案,只需要发放学习资料即可.
21.【详解】(1)解:由正弦定理知,,∵,代入上式得,
∵,∴,,∵,∴.
(2)若选①:由平分得,,
∴,即.
在中,由余弦定理得,又,∴,
联立得,解得,(舍去),
∴.
若选②:因为,,
,得,在中,由余弦定理得,即,联立,可得,
∴.
22.【详解】(1)证明:连结交交于,
∵是正方形,∴为的中点,
又∵是的中点,∴,
又∵平面,平面,∴平面,
又平面,平面平面,∴.
(2)∵平面,平面,
∴,
设正方形的边长为4,
∵,
∴的中线,,,
同理,,,
∵,,
∴为正三角形,中线,且,
∵,,
∴,同理,
∴是二面角的一个平面角,
又∵在正三角形中,
∴,
则平面与平面所成的较小的面角的余弦值为.
(3)同(2)中,得,
又∵在正方形中,,,平面,平面,
∴平面,
同理平面,
同理面,
∴是直线与平面所成的角,
∵在和中得,
∴直线与平面所成角的正切值为.
数学试题
一、单项选择题:本大题共8小题.每小题5分,共40分.
1.复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知平面向量,,与垂直,则的值是( )
A. B.1 C. D.2
3.若一个圆锥的底面面积为,其侧面展开图是圆心角为的扇形,则该圆锥的体积为( )
A. B. C. D.
4.若m,n,为三条不同的直线,,为两个不重合的平面,则下列命题正确的是( )
A.如果,,则 B.如果,,m||,n||,则
C.如果,,则 D.如果,,,则
5.一个人连续射击次,则下列各事件关系中,说法正确的是( )
A.事件“两次均击中”与事件“至少一次击中”互为对立事件
B.事件“第一次击中”与事件“第二次击中”为互斥事件
C.事件“两次均未击中”与事件“至多一次击中”互为对立事件
D.事件“恰有一次击中”与事件“两次均击中”为互斥事件
6.某校为了解学生每个月在图书馆借阅书籍的数量,图书管理员甲抽取了一个容量为100的样本,并算得样本的平均数为5,方差为9;图书管理员乙也抽取了一个容量为100的样本,并算得样本的平均数为7,方差为16.若将这两个样本合在一起组成一个容量为200的新样本,则新样本数据的( )
A.平均数为6 B.平均数为6.5 C.方差为12.5 D.方差为13
7.如图,AB是底部B不可到达的一座建筑物,
A为建筑物的最高点,为了测量建筑物高度AB,我们选择一条水平基线HG,使H,G,B三点在同一直线上,经测量,在G,H两点用测角仪器测得A的仰角分别是,,米,测角仪器的高是1.5米,则该建筑物的高AB约为( )(参考数据:)
A.13.5米 B.14.2米 C.15.2米 D.16.5米
8.在三棱锥中,平面平面BCD,是以CD为斜边的等腰直角三角形,M为CD中点,,,则该三棱锥的外接球的表面积为( )
A. B. C. D.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)
9.下列说法正确的是( )
A.向量在向量上的投影向量可表示为
B.若,则与的夹角θ的范围是
C.若,,则
D.已知,,则
10.近年,随着人工智能,AIoT,云计算等技术的推动,全球数据量正在无限制地扩展和增加.国际数据公司IDC统计了2016~2020年全球每年产生的数据量及其增速,所得结果如图所示,根据该统计图,下列说法正确的是( )
A.2016~2020年,全球每年产生的数据量在持续增加
B.2016~2020年,全球数据量的年平均增长率持续下降
C.2016~2020年,全球每年产生的数据量的平均数为33.7
D.2015年,全球产生的数据量超过15
11.已知a,b,c分别是三个内角A,B,C的对边,则下列命题中正确的是( )
A.若,则
B.若是边长为1的正三角形,则
C.若,,,则有一解
D.若是所在平面内的一点,且,则是直角三角形
12.正方体中,E是棱的中点,F在侧面上运动,且满足平面.以下命题正确的有( )
A.侧面上存在点F,使得
B.直线与直线所成角可能为
C.平面与平面所成锐二面角的正切值为
D.设正方体棱长为1,则过点E,F,A的平面截正方体所得的截面面积最大为
三、填空题:本大题共4小题,每小题5分,共20分.
13.已知一组数据8.6,8.9,9.1,9.6,9.7,9.8,9.9,10.2,10.6,10.8,11.2,11.7,则该组数据的第80百分位数为__________.
14.如图,是斜二测画法画出的水平放置的的直观图,是的中点,且轴,轴,,,则的周长______.
15.在中,为中点,若,则实数的值为___________.
16..如图, 二面角的平面角的大小为为半平面内的两个点, 为半平面内一点, 且, 若直线与平面所成角为为的中点, 则线段长度的最大值是___________.
、
四.解答题:本大题共6小题,共70分.
17.(10分).已知某校高一、高二、高三三个年级的学生志愿者人数分别为180,120,120.现采用样本按比例分配的分层随机抽样方法,从中抽取7名同学去敬老院参加献爱心活动.
(1)应从高一、高二、高三三个年级的学生志愿者中分别抽取多少人?
(2)抽出的7名同学分别用A,B,C,D,E,F,G表示,现从该7名同学中随机抽取2名同学承担敬老院卫生打扫工作.设7名同学中来自高一的3人分别为A,B,C,记事件“抽取的两名同学中至少有一名来自高一年级”,试用所给字母写出事件M包含的样本点;
18(12分).的内角的对边分别为,,且______.
在①,②,这两个条件中任选一个,补充在横线中,并解答.
注:如果选择多个条件分别解答,按第一个解答计分.
(1)求的面积;
(2)若,求.
19.(12分)在如图所示的四棱锥中,四边形是等腰梯形,,平面,.
(1)求证:;
(2)若为的中点,问线段上是否存在点,使得平面?若存在,求出的长;若不存在,请说明理由.
20.(12分)2021年中国共产党迎来了建党100周年,为了铭记建党历史、缅怀革命先烈、增强爱国主义情怀,某学校为学生组织了系列学党史活动.为了解学生的学习情况,从全校学生中随机抽取了n名同学进行党史知识测试,满分100分,并将这名同学的测试成绩按,,,,分成5组,绘制成了如图所示的频率分布直方图.已知测试成绩在的学生为70人.
(1)求的值及频率分布直方图中的值;
(2)为奖励优胜者,学校将对本次测试成绩排在前40%的学生发放奖品,若某学生获得了奖品,请估算一下该学生的成绩至少达到多少分;
(3)学校组织党史知识测试设定的预案是:以抽取的样本作为参考,若学生的平均成绩不低于80分,只需发放下一步学习资料,否则要举办党史知识大讲堂加强学习.请根据所学的统计知识,估计该校是否需要举办党史知识大讲堂,并说明理由.(同一组中的数据以这组数据所在区间中点的值作代表)
21.(12分)在△ABC中,角A,B,C的对边分别是a,b,c,且.
(1)求角B的大小;
(2)若,D为AC边上的一点,,且__________ ,求△ABC的面积.
请在下列两个条件中选择一个作为条件补充在横线上,并解决问题.
①BD是∠ABC的平分线;②D为线段AC的中点.
(注:如果选择多个条件分别解答,则按第一个解答记分.)
22.(12分)如图,四棱锥的底面是正方形,平面,.点是的中点,作,交于点.
(1)设平面与平面的交线为,试判断直线与直线的位置关系,并给出证明;
(2)求平面与平面所成的较小的二面角的余弦值;
(3)求直线与平面所成角的正切值.
高一第二学期第三次阶段性测试数学试题答案
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项 D A B C D A C D AB ACD AD AC
13.10.8. 14.. 15. 16.
8.【详解】因为是以CD为斜边的等腰直角三角形,M为CD中点,,
所以AM⊥CD,且,
因为,所以,而,
由勾股定理得:,所以BM=BC,
故为等腰直角三角形,,,由题意得:球心O在平面ACD的投影与M点重合,因为平面平面BCD,所以球心O在平面BCD上,在平面BCD上,过点M作MH⊥CD,故,
球心O在MH上,设OM=x,由余弦定理得:,则,
由得:,解得:,设外接球半径为,则,
故该三棱锥的外接球的表面积为.
12.【详解】取中点M,中点N,连接,则易证得,,从而平面平面,所以点F的运动轨迹为线段.
取的中点F,因为是等腰三角形,所以,又因为,所以,故A正确;设正方体的棱长为a,当点F与点M或点N重合时,直线与直线所成角最大,此时,所以B错误;
平面平面,取F为的中点,则,,∴即为平面与平面所成的锐二面角,,所以C正确;
因为当F为与的交点时,截面为菱形(为的中点),面积为,故D错误.
16..【详解】如图,自点引平面的垂线,垂足为,因为,
则A,B两点在以CO为高以CA,CB为母线的圆锥的底面圆周上,所以当A,B
两点运动到公共棱上时AD最大.
自点引公共棱的垂线OH,则,不难解出,在中,由余弦定理得:,
又在中由余弦定理得:
17.解析:(1)由题意知,高一、高二、高三,三个年级的学生志愿者人数之比为,又采用样本量按比例分配的分层随机抽样方法,从中抽取7名同学.
故应从高一、高二、高三,三个年级的学生志愿者中分别抽取3人,2人,2人.
,,,,,,,,,,,,,,,共含有15个样本点.
18.【详解】(1)若选①:因为,由余弦定理得,整理得,则,又,则,,则;
若选②:因为,即,则,又,则,又,得,
则;
(2)由正弦定理得:,,
则,.
19.(1)证明:因为四边形是等腰梯形,,所以,因为,所以,因为,所以所以在中,,即,因为平面,平面,所以,因为,平面,所以平面,因为平面,所以.
(2)解:线段上存在点,使得平面,.下面证明结论:如图,取中点,连接,在线段上取点,使得,连接,由(1)知,在中,,,所以,因为,,所以,因为为中点,为的中点,所以,所以,所以四边形为平行四边形,所以,因为平面,平面,所以平面.所以线段上存在点,使得平面,.
20.【详解】(1)由已知条件可得,由频率和为1得,解得.
(2)因为,所以问题转化为估计样本数据的第60百分位数,
因为,
,所以第60百分位数在区间内,设该生得分最低为,则,
解得,所以估计该生的得分至少达到86分.
(3)由频率分布直方图可得
,因为,
所以按照学校的预案,只需要发放学习资料即可.
21.【详解】(1)解:由正弦定理知,,∵,代入上式得,
∵,∴,,∵,∴.
(2)若选①:由平分得,,
∴,即.
在中,由余弦定理得,又,∴,
联立得,解得,(舍去),
∴.
若选②:因为,,
,得,在中,由余弦定理得,即,联立,可得,
∴.
22.【详解】(1)证明:连结交交于,
∵是正方形,∴为的中点,
又∵是的中点,∴,
又∵平面,平面,∴平面,
又平面,平面平面,∴.
(2)∵平面,平面,
∴,
设正方形的边长为4,
∵,
∴的中线,,,
同理,,,
∵,,
∴为正三角形,中线,且,
∵,,
∴,同理,
∴是二面角的一个平面角,
又∵在正三角形中,
∴,
则平面与平面所成的较小的面角的余弦值为.
(3)同(2)中,得,
又∵在正方形中,,,平面,平面,
∴平面,
同理平面,
同理面,
∴是直线与平面所成的角,
∵在和中得,
∴直线与平面所成角的正切值为.
同课章节目录
