2022-2023学年人教版数学九年级下册27.2相似三角形(课时6)同步练习(含解析)
文档属性
| 名称 | 2022-2023学年人教版数学九年级下册27.2相似三角形(课时6)同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 257.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 16:54:34 | ||
图片预览


文档简介
《27.2 相似三角形》同步练习
(课时6 相似三角形的性质)
一、基础巩固
知识点1 相似三角形对应线段的比等于相似比
1. [2021上海浦东新区期中]如果两个相似三角形对应角平分线的比是2∶3,那么它们的对应边的比是( )
A.2∶3 B.4∶9 C.16∶81 D.
2. 已知△ABC∽△DEF,且相似比为4∶3,若△ABC中BC边上的中线AM=8,则△DEF中EF边上的中线DN= ( )
A.3 B.4 C.5 D.6
3. 如图,△ABC∽△A'B'C',AD,BE分别是△ABC的高和中线,A'D',B'E'分别是△A'B'C'的高和中线,且AD=4,A'D'=3,BE=6,则B'E'的长为 .
知识点2 相似三角形周长的比等于相似比
4. [2021河北唐山路北区期末]已知△ABC与△A1B1C1相似,且相似比为3∶2,则△ABC与△A1B1C1的周长比为 ( )
A.1∶1 B.3∶2 C.3∶1 D.9∶4
5. [2021天津滨海新区期末]已知△ABC与△DEF相似,且对应高线之比为2∶3,若△ABC的周长为40,则△DEF的周长是( )
A.10 B.20 C.40 D.60
6. 如图,已知矩形ABCD的边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与边BC交于点O.
(1)求证:△OCP∽△PDA.
(2)若△OCP与△PDA的周长比为1∶2,求边AB的长.
知识点3 相似三角形面积的比等于相似比的平方
7. [2021河北石家庄二十八中一模]在一张复印出来的纸上,一个三角形的一条边由原图中的2 cm变成了6 cm,则复印出的三角形的面积是原图中三角形面积的 ( )
A.3倍 B.6倍 C.9倍 D.12倍
8. [2021河南漯河郾城区期末]如图,在△ABC中,CD,BE是△ABC的边AB,AC上的中线,则=( )
A. B. C. D.
9. [2021江苏徐州中考]如图,在△ABC中,点D,E分别在边BA,BC上,且==,△DBE与四边形ADEC的面积的比为 .
10. 如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,且∠ABC=2∠BAM.
(1)求证:AG=BG.
(2)若 M为BC的中点,同时S△BGM=1,求△ADG的面积.
二、能力提升
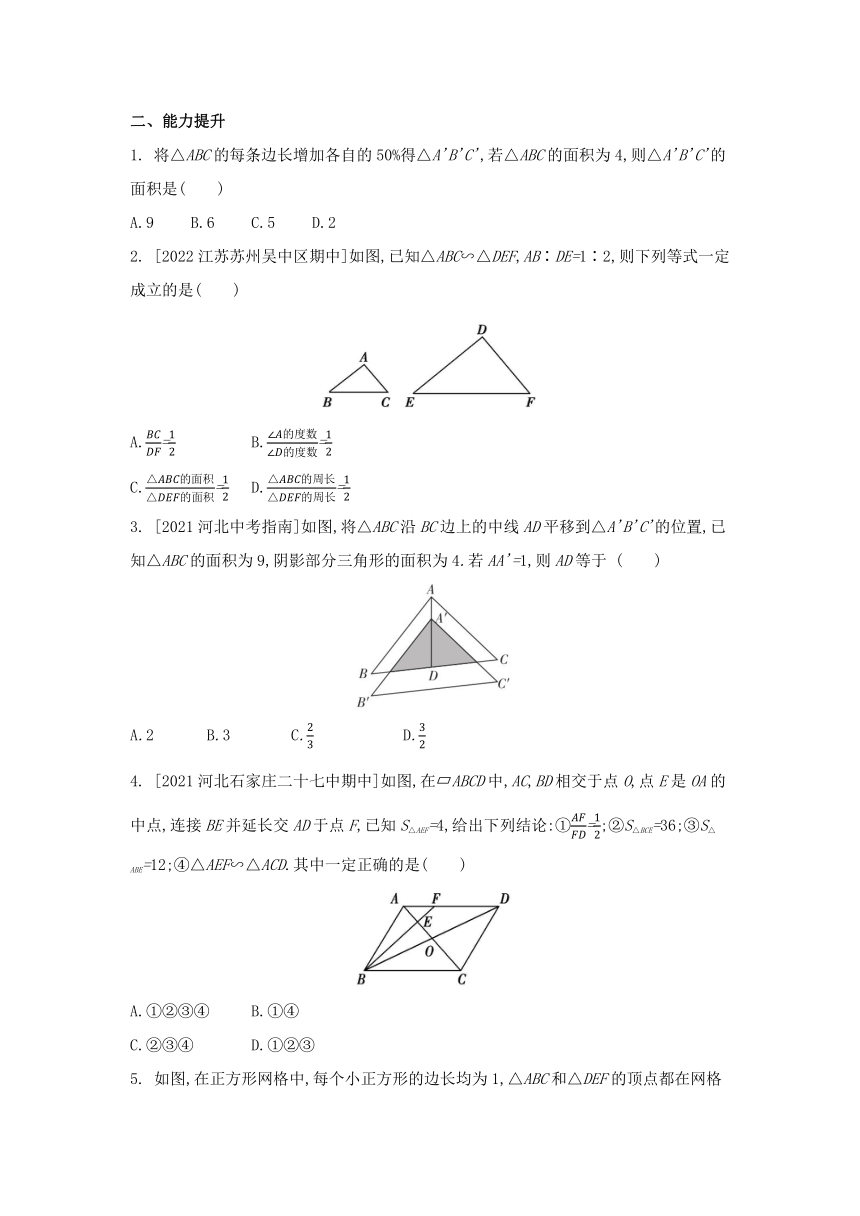
1. 将△ABC的每条边长增加各自的50%得△A'B'C',若△ABC的面积为4,则△A'B'C'的面积是( )
A.9 B.6 C.5 D.2
2. [2022江苏苏州吴中区期中]如图,已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A.= B.=
C.= D.=
3. [2021河北中考指南]如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则AD等于 ( )
A.2 B.3 C. D.
4. [2021河北石家庄二十七中期中]如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,给出下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是( )
A.①②③④ B.①④
C.②③④ D.①②③
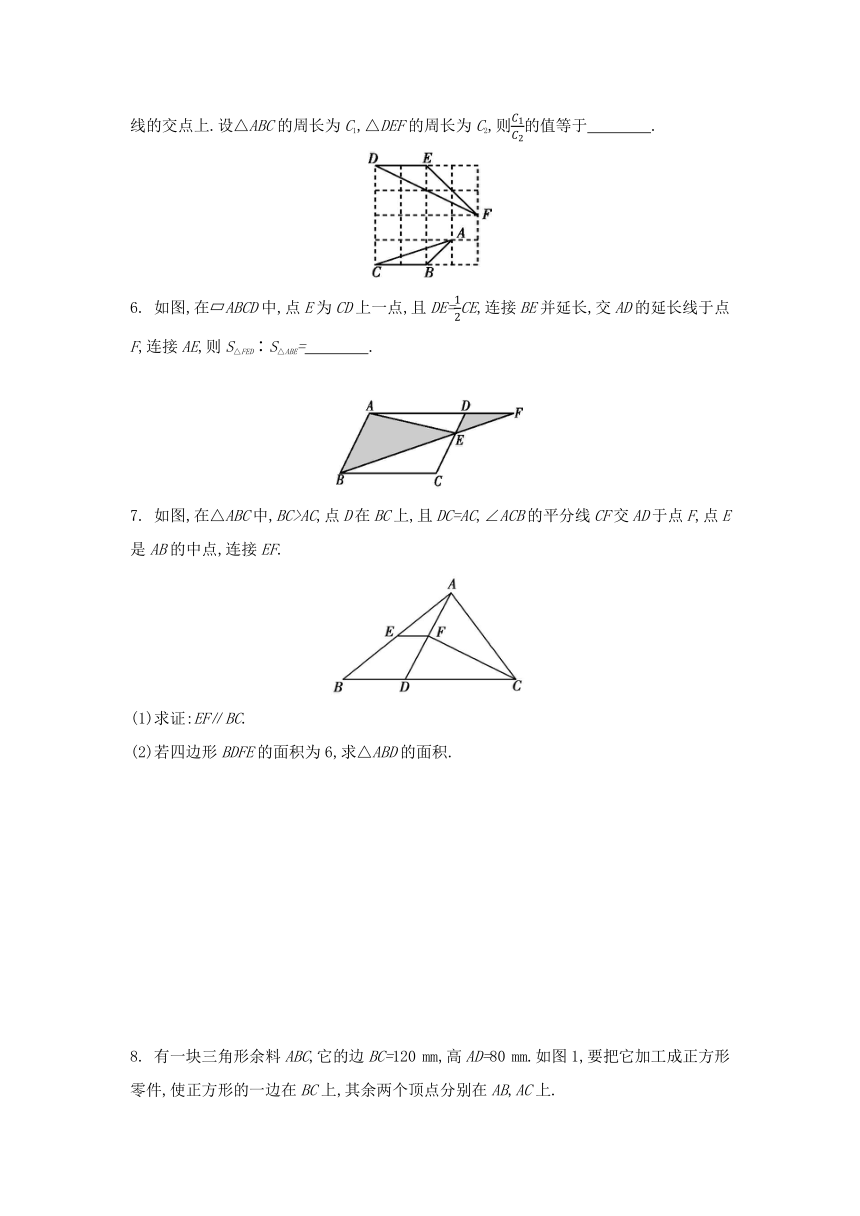
5. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .
6. 如图,在 ABCD中,点E为CD上一点,且DE=CE,连接BE并延长,交AD的延长线于点F,连接AE,则S△FED∶S△ABE= .
7. 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
8. 有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.如图1,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求加工成的正方形零件的边长.
(2)如果要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形组成,如图2,此时,这个矩形零件的两条边长分别为多少
(3)如果要加工的零件只是一个矩形,如图3,此时,这个矩形零件的两条边长不能确定,但这个矩形的面积有最大值,求面积达到最大值时矩形零件的两条边长.
参考答案
一、基础巩固
1.A 【解析】 由两个相似三角形对应角平分线的比是2∶3,知它们的相似比是2∶3,故它们的对应边的比是2∶3.
2.D 【解析】 ∵△ABC∽△DEF,相似比为4∶3,∴=,∵AM=8,∴DN=6.
3. 【解析】 因为△ABC∽△A'B'C',所以=,因为AD=4,A'D'=3,BE=6,所以B'E'=.
4.B 【解析】 根据相似三角形的周长比等于相似比,知△ABC与△A1B1C1的周长比为3∶2.
5.D 【解析】 易知△ABC与△DEF的相似比为2∶3,∴△ABC的周长∶△DEF的周长=2∶3,∴△DEF的周长为×40=60.
6.【解析】 (1)∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°.
由折叠的性质,可得∠APO=∠B=90°,
∴∠APD=90°-∠CPO=∠POC.
∴△OCP∽△PDA.
(2)∵△OCP与△PDA的周长比为1∶2,
∴==,∴PA=2OP,DA=2CP.
∵AD=8,∴CP=4,BC=8.
设OP=x,则OB=x,OC=8-x.
在Rt△PCO中,∠C=90°,CP=4,OP=x,OC=8-x,
∴x2=(8-x)2+42,∴x=5.∴AB=AP=2OP=10.
7.C 【解析】 由题意,得复印出的三角形与原图中的三角形相似,且相似比为=,所以它们的面积比为()2=,故复印出的三角形的面积是原图中三角形面积的9倍.
8.D 【解析】 ∵CD,BE是△ABC的边AB,AC上的中线,∴DE是△ABC的中位线,∴DE∥BC,且DE=BC,∴△DEF∽△CBF,且相似比为,∴=.
9. 【解析】 要求△DBE与四边形ADEC的面积的比,需求△DBE与△ABC的面积的比,根据相似三角形面积的比等于对应边的比的平方进行求解.
10.【解析】 (1)∵四边形ABCD为菱形,
∴BD平分∠ABC,∴∠ABC=2∠ABG,
又∠ABC=2∠BAM,∴∠BAM=∠ABG,∴AG=BG.
(2)∵四边形ABCD为菱形,∴AD∥BC,AD=BC,
∴△BGM∽△DGA.
∵M为BC的中点,∴BM=BC=AD.
∴△BGM与△DGA的相似比为1∶2,∴S△BGM∶S△DGA=1∶4.
∵S△BGM=1,∴S△DGA=4,即△ADG的面积为4.
二、能力提升
1.A 【解析】 ∵将△ABC的每条边长增加各自的50%得△A'B'C',
∴△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为=,∴=()2=.∵△ABC的面积为4,∴△A'B'C'的面积是9.
2.D 【解析】 ∵△ABC∽△DEF,AB∶DE=1∶2,∴=,=1,=,
=.
3.B 【解析】 如图,∵S△ABC=9,S△A'EF=4,且AD为BC边的中线,∴S△A'DE=S△A'EF=2,S△ABD=S△ABC=.∵将△ABC沿BC边上的中线AD平移得到△A'B'C',∴A'E∥AB,
∴△DA'E∽△DAB,∴()2=,即()2=,∴A'D=2,∴AD=AA'+A'D=3.
4.D 【解析】 ∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,AO=AC,∵点E是OA的中点,∴AE=CE.∵AD∥BC,∴△AFE∽△CBE,∴==.∵AD=BC,∴AF=AD,∴=,故①正确;∵△AFE∽△CBE,=,∴S△BCE=9S△AEF=36,故②正确;∵△AFE∽△CBE,=,
∴=,∴S△ABE=3S△AEF=12,故③正确;∵BF与CD不平行,∴④错误.
5. 【解析】 因为==,==,==,所以==
=,所以△DEF∽△ABC,所以==.
6.1∶6 【解析】 设S ABCD=a,则S△ABE=a,S△ADE+S△BCE=a.∵DE=CE,∴S△ADE∶S△BCE=1∶2,
∴S△BCE=a=a.∵AD∥BC,∴△DFE∽△CBE,∴=()2=,∴S△FDE=a=a,∴S△FED∶S△ABE=a∶a=1∶6.
7.【解析】 (1)∵DC=AC,CF平分∠ACB,
∴CF是△ACD的中线,∴点F是AD的中点,
又点E是AB的中点,∴EF∥BD,即 EF∥BC.
(2)由(1)知EF∥BD, ∴△AEF∽△ABD,∴ =()2.
∵AE=AB, S△AEF=S△ABD-S四边形BDFE=S△ABD-6,
∴=()2 ,∴S△ABD=8,即△ABD的面积为8.
8.【解析】 (1)设正方形零件的边长为x mm,则PN=PQ=ED=x mm,
∴AE=AD-ED=(80-x)mm.
∵PN∥BC,∴△APN∽△ABC,
∴=,即=,解得x=48.
∴加工成的正方形零件的边长是48 mm.
(2)设PQ=y mm,则PN=2y mm,AE=(80-y)mm,
∵PN∥BC,∴△APN∽△ABC,
∴=,即=,解得y=,∴2y=.
∴这个矩形零件的两条边长分别为 mm, mm.
(课时6 相似三角形的性质)
一、基础巩固
知识点1 相似三角形对应线段的比等于相似比
1. [2021上海浦东新区期中]如果两个相似三角形对应角平分线的比是2∶3,那么它们的对应边的比是( )
A.2∶3 B.4∶9 C.16∶81 D.
2. 已知△ABC∽△DEF,且相似比为4∶3,若△ABC中BC边上的中线AM=8,则△DEF中EF边上的中线DN= ( )
A.3 B.4 C.5 D.6
3. 如图,△ABC∽△A'B'C',AD,BE分别是△ABC的高和中线,A'D',B'E'分别是△A'B'C'的高和中线,且AD=4,A'D'=3,BE=6,则B'E'的长为 .
知识点2 相似三角形周长的比等于相似比
4. [2021河北唐山路北区期末]已知△ABC与△A1B1C1相似,且相似比为3∶2,则△ABC与△A1B1C1的周长比为 ( )
A.1∶1 B.3∶2 C.3∶1 D.9∶4
5. [2021天津滨海新区期末]已知△ABC与△DEF相似,且对应高线之比为2∶3,若△ABC的周长为40,则△DEF的周长是( )
A.10 B.20 C.40 D.60
6. 如图,已知矩形ABCD的边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的点P处,折痕与边BC交于点O.
(1)求证:△OCP∽△PDA.
(2)若△OCP与△PDA的周长比为1∶2,求边AB的长.
知识点3 相似三角形面积的比等于相似比的平方
7. [2021河北石家庄二十八中一模]在一张复印出来的纸上,一个三角形的一条边由原图中的2 cm变成了6 cm,则复印出的三角形的面积是原图中三角形面积的 ( )
A.3倍 B.6倍 C.9倍 D.12倍
8. [2021河南漯河郾城区期末]如图,在△ABC中,CD,BE是△ABC的边AB,AC上的中线,则=( )
A. B. C. D.
9. [2021江苏徐州中考]如图,在△ABC中,点D,E分别在边BA,BC上,且==,△DBE与四边形ADEC的面积的比为 .
10. 如图,四边形ABCD为菱形,M为BC上一点,连接AM交对角线BD于点G,且∠ABC=2∠BAM.
(1)求证:AG=BG.
(2)若 M为BC的中点,同时S△BGM=1,求△ADG的面积.
二、能力提升
1. 将△ABC的每条边长增加各自的50%得△A'B'C',若△ABC的面积为4,则△A'B'C'的面积是( )
A.9 B.6 C.5 D.2
2. [2022江苏苏州吴中区期中]如图,已知△ABC∽△DEF,AB∶DE=1∶2,则下列等式一定成立的是( )
A.= B.=
C.= D.=
3. [2021河北中考指南]如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则AD等于 ( )
A.2 B.3 C. D.
4. [2021河北石家庄二十七中期中]如图,在 ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,给出下列结论:①=;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD.其中一定正确的是( )
A.①②③④ B.①④
C.②③④ D.①②③
5. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1,△DEF的周长为C2,则的值等于 .
6. 如图,在 ABCD中,点E为CD上一点,且DE=CE,连接BE并延长,交AD的延长线于点F,连接AE,则S△FED∶S△ABE= .
7. 如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
(1)求证:EF∥BC.
(2)若四边形BDFE的面积为6,求△ABD的面积.
8. 有一块三角形余料ABC,它的边BC=120 mm,高AD=80 mm.如图1,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)求加工成的正方形零件的边长.
(2)如果要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形组成,如图2,此时,这个矩形零件的两条边长分别为多少
(3)如果要加工的零件只是一个矩形,如图3,此时,这个矩形零件的两条边长不能确定,但这个矩形的面积有最大值,求面积达到最大值时矩形零件的两条边长.
参考答案
一、基础巩固
1.A 【解析】 由两个相似三角形对应角平分线的比是2∶3,知它们的相似比是2∶3,故它们的对应边的比是2∶3.
2.D 【解析】 ∵△ABC∽△DEF,相似比为4∶3,∴=,∵AM=8,∴DN=6.
3. 【解析】 因为△ABC∽△A'B'C',所以=,因为AD=4,A'D'=3,BE=6,所以B'E'=.
4.B 【解析】 根据相似三角形的周长比等于相似比,知△ABC与△A1B1C1的周长比为3∶2.
5.D 【解析】 易知△ABC与△DEF的相似比为2∶3,∴△ABC的周长∶△DEF的周长=2∶3,∴△DEF的周长为×40=60.
6.【解析】 (1)∵四边形ABCD是矩形,∴∠B=∠C=∠D=90°.
由折叠的性质,可得∠APO=∠B=90°,
∴∠APD=90°-∠CPO=∠POC.
∴△OCP∽△PDA.
(2)∵△OCP与△PDA的周长比为1∶2,
∴==,∴PA=2OP,DA=2CP.
∵AD=8,∴CP=4,BC=8.
设OP=x,则OB=x,OC=8-x.
在Rt△PCO中,∠C=90°,CP=4,OP=x,OC=8-x,
∴x2=(8-x)2+42,∴x=5.∴AB=AP=2OP=10.
7.C 【解析】 由题意,得复印出的三角形与原图中的三角形相似,且相似比为=,所以它们的面积比为()2=,故复印出的三角形的面积是原图中三角形面积的9倍.
8.D 【解析】 ∵CD,BE是△ABC的边AB,AC上的中线,∴DE是△ABC的中位线,∴DE∥BC,且DE=BC,∴△DEF∽△CBF,且相似比为,∴=.
9. 【解析】 要求△DBE与四边形ADEC的面积的比,需求△DBE与△ABC的面积的比,根据相似三角形面积的比等于对应边的比的平方进行求解.
10.【解析】 (1)∵四边形ABCD为菱形,
∴BD平分∠ABC,∴∠ABC=2∠ABG,
又∠ABC=2∠BAM,∴∠BAM=∠ABG,∴AG=BG.
(2)∵四边形ABCD为菱形,∴AD∥BC,AD=BC,
∴△BGM∽△DGA.
∵M为BC的中点,∴BM=BC=AD.
∴△BGM与△DGA的相似比为1∶2,∴S△BGM∶S△DGA=1∶4.
∵S△BGM=1,∴S△DGA=4,即△ADG的面积为4.
二、能力提升
1.A 【解析】 ∵将△ABC的每条边长增加各自的50%得△A'B'C',
∴△ABC∽△A'B'C',△ABC与△A'B'C'的相似比为=,∴=()2=.∵△ABC的面积为4,∴△A'B'C'的面积是9.
2.D 【解析】 ∵△ABC∽△DEF,AB∶DE=1∶2,∴=,=1,=,
=.
3.B 【解析】 如图,∵S△ABC=9,S△A'EF=4,且AD为BC边的中线,∴S△A'DE=S△A'EF=2,S△ABD=S△ABC=.∵将△ABC沿BC边上的中线AD平移得到△A'B'C',∴A'E∥AB,
∴△DA'E∽△DAB,∴()2=,即()2=,∴A'D=2,∴AD=AA'+A'D=3.
4.D 【解析】 ∵四边形ABCD为平行四边形,∴AD∥BC,AD=BC,AO=AC,∵点E是OA的中点,∴AE=CE.∵AD∥BC,∴△AFE∽△CBE,∴==.∵AD=BC,∴AF=AD,∴=,故①正确;∵△AFE∽△CBE,=,∴S△BCE=9S△AEF=36,故②正确;∵△AFE∽△CBE,=,
∴=,∴S△ABE=3S△AEF=12,故③正确;∵BF与CD不平行,∴④错误.
5. 【解析】 因为==,==,==,所以==
=,所以△DEF∽△ABC,所以==.
6.1∶6 【解析】 设S ABCD=a,则S△ABE=a,S△ADE+S△BCE=a.∵DE=CE,∴S△ADE∶S△BCE=1∶2,
∴S△BCE=a=a.∵AD∥BC,∴△DFE∽△CBE,∴=()2=,∴S△FDE=a=a,∴S△FED∶S△ABE=a∶a=1∶6.
7.【解析】 (1)∵DC=AC,CF平分∠ACB,
∴CF是△ACD的中线,∴点F是AD的中点,
又点E是AB的中点,∴EF∥BD,即 EF∥BC.
(2)由(1)知EF∥BD, ∴△AEF∽△ABD,∴ =()2.
∵AE=AB, S△AEF=S△ABD-S四边形BDFE=S△ABD-6,
∴=()2 ,∴S△ABD=8,即△ABD的面积为8.
8.【解析】 (1)设正方形零件的边长为x mm,则PN=PQ=ED=x mm,
∴AE=AD-ED=(80-x)mm.
∵PN∥BC,∴△APN∽△ABC,
∴=,即=,解得x=48.
∴加工成的正方形零件的边长是48 mm.
(2)设PQ=y mm,则PN=2y mm,AE=(80-y)mm,
∵PN∥BC,∴△APN∽△ABC,
∴=,即=,解得y=,∴2y=.
∴这个矩形零件的两条边长分别为 mm, mm.
