测量旗杆的高度[下学期]

课件16张PPT。北师大版八年级数学下册
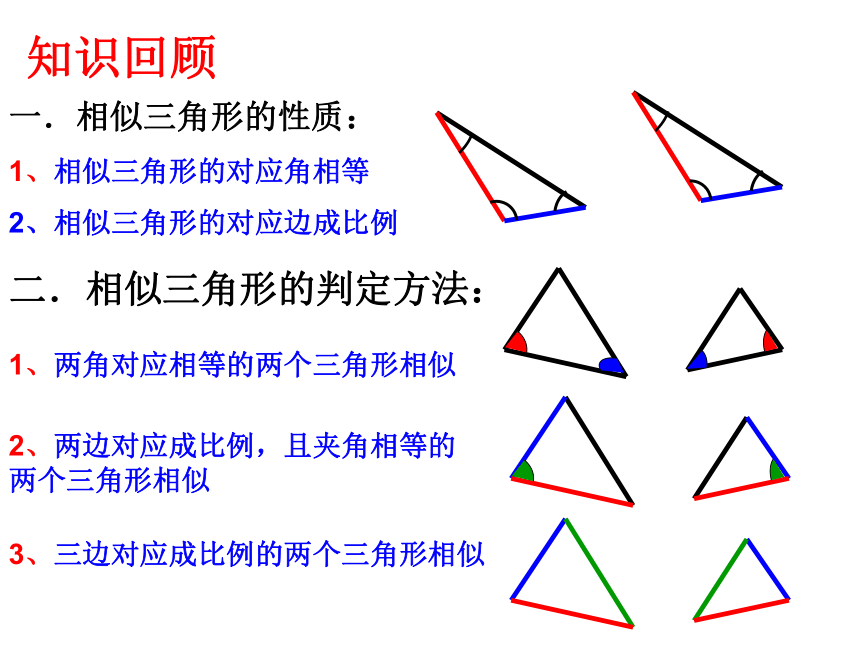
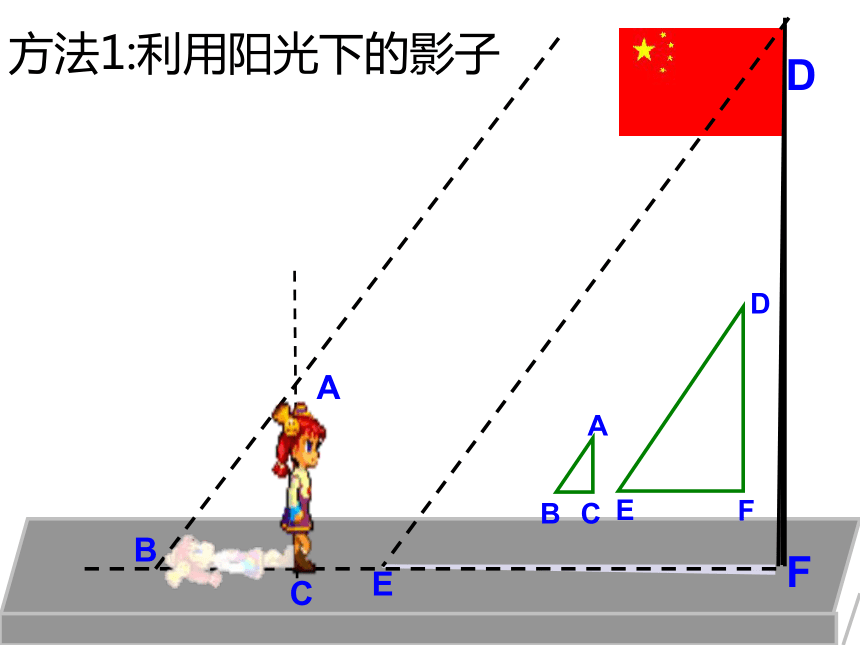
第四章第七节测量旗杆的高度知识回顾二．相似三角形的判定方法：1、两角对应相等的两个三角形相似3、三边对应成比例的两个三角形相似2、两边对应成比例，且夹角相等的两个三角形相似方法1:利用阳光下的影子 ∵太阳的光线是平行的
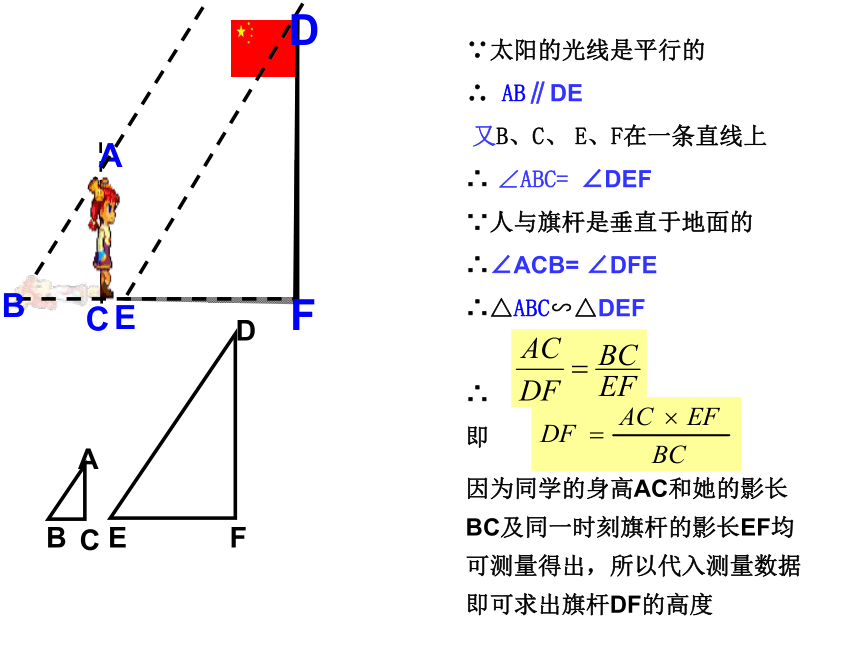
∴ AB∥DE
又B、C、 E、F在一条直线上
∴ ∠ABC= ∠DEF
∵人与旗杆是垂直于地面的
∴∠ACB= ∠DFE
∴△ABC∽△DEF
∴
即
因为同学的身高AC和她的影长BC及同一时刻旗杆的影长EF均可测量得出，所以代入测量数据即可求出旗杆DF的高度
例1、小敏测得2m高的标杆在太阳光下的影长为1.2m，同时又测得一颗树的影长为12m，请你计算出这棵树的高度。解：如图所示：
AC表示标杆，BC表示标杆的影长，DF表示树高，由题意知：
△ ABC∽ △ DEF
∴
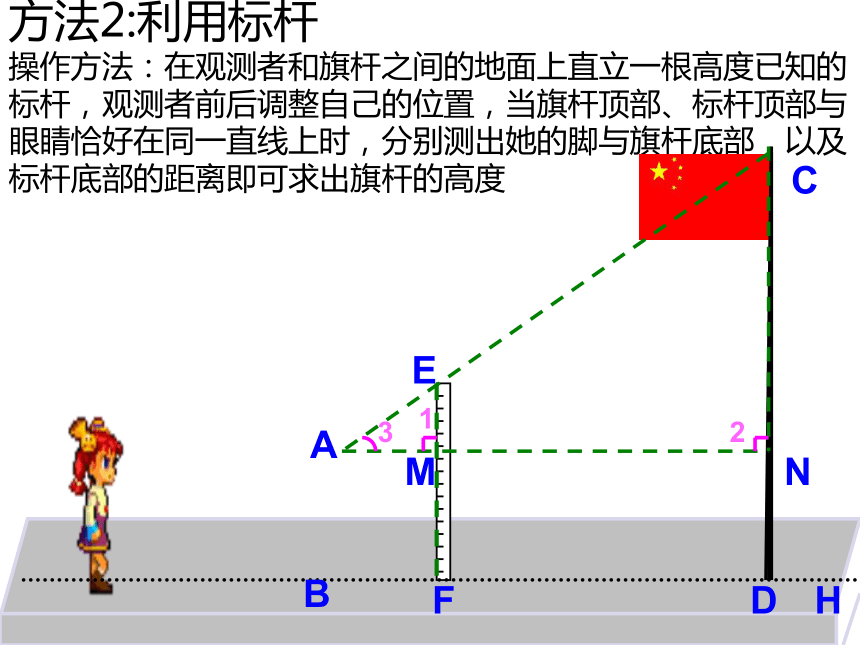
∴ DF=20∴ 所以树的高度为20米方法2:利用标杆操作方法：在观测者和旗杆之间的地面上直立一根高度已知的标杆，观测者前后调整自己的位置，当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时，分别测出她的脚与旗杆底部，以及标杆底部的距离即可求出旗杆的高度方法3、利用镜子的反射操作方法：选一名学生作为观测者，在她与旗杆之间的地面上平放一面镜子，固定镜子的位置，观测者看着镜子来回调整自己的位置，使自己能够通过镜子看到旗杆顶端，测出此时她的脚与镜子的距离、旗杆底部与镜子的距离就能求出旗杆的高度。
例2、如图，在距离树高AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处，在镜子里恰看见树顶。若人眼距地面1.4米，求树高。 解：由题意知：BE=18米、DE=2.1米、CD=1.4米，且△ ABE∽ △ CDE
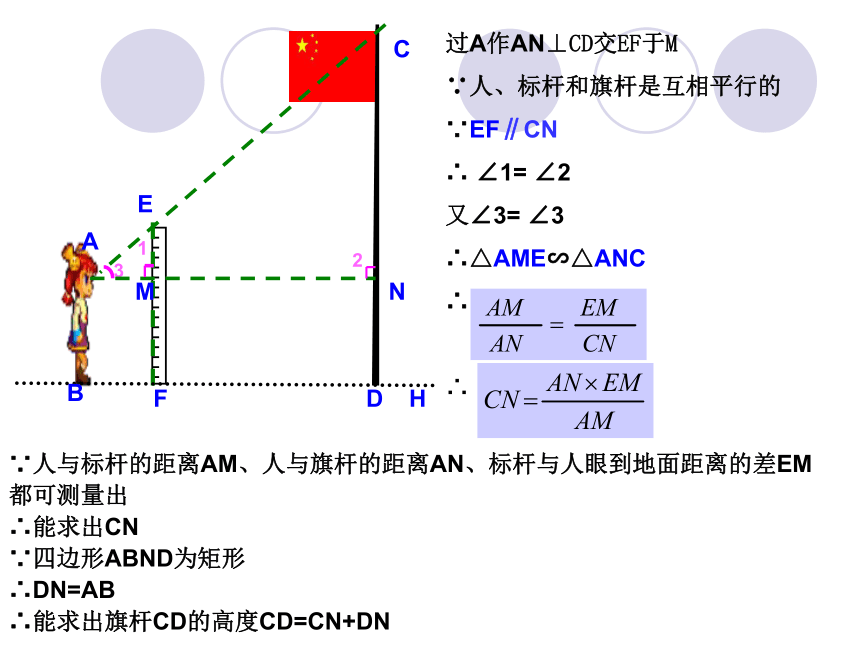
AB= 12 所以树高为12米∴∴∴如图，A、B两点分别位于一个池塘的两端，小芳想用绳子测量A、B两点之间的距离，但绳子的长度不够，一位同学帮她想了一个主意，先在地上取一个可以直接到达A、B点的点C，找到AC、BC的中点D、E，并且DE的长为5m，则A、B两点的距离是多少？CBAED 练习例 小明为测量一棵树CD的高度，他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置，当他与树相距27m时，他的眼睛、标杆的顶端和树顶端在同一直线上，已知小明身高1.6m,求树的高度。解：过点A作AN ∥BD交CD于N、EF于M
∵人、标杆、树都垂直于地面
∴∠ABF=∠EFD =∠CDF=90o∴ AB ∥EF ∥CD
∴∠EMA=∠CNA
∵ ∠EAM=∠CAN
∴△AEM∽△CAN∴ CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m实践探索：
一油桶高0.8m，桶内有油，一根木棒长1米，从桶盖小口斜插入桶内一端到桶底，另一端到小口，抽出木棒，量得棒上浸油部分长为0.8m，则桶内油面的高度为多少米？0.64米ABCDE拓展训练 某同学想测旗杆的高度，他在某一时刻测得1m长的竹竿竖直时的影长为1.5m，同一时刻测量旗杆影长时，因旗杆靠近一幢楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为9m，留在墙上的影长为2m，求旗杆的高度。作业：一个盗窃犯夜深人静之时潜入某单位作案，该单位的自动摄像系统摄下了他作案的全过程。请你为警方设计一个方案，估计该盗窃犯的大致身高