第八章成对数据的统计分析 章节检测(无答案)
文档属性
| 名称 | 第八章成对数据的统计分析 章节检测(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 527.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-13 21:18:14 | ||
图片预览


文档简介
人教A版高中数学选择性必修第三册 第八章 成对数据的统计分析 章节检测
一、单选题
1.某产品的宣传费用(万元)与销售额(万元)的统计数据如下表所示:
宣传费用(万元) 3 1 2 6
销售额(万元) 10 4 16
根据上表可得回归方程,则宣传费用为2万元时销售额为( )
A.4 B.5 C.6 D.7
2.已知变量与负相关,且由观测数据算得样本平均数,,则由该观测数据算得的线性回归方程可能是( )
A. B.
C. D.
3.下列说法正确的是( )
A.“A与B是互斥事件”是“A与B互为对立事件”的充分不必要条件
B.设具有线性相关关系的两个变量x,y的相关系数为r,则越接近于0,x,y之间线性相关程度越强
C.已知随机变量X的方差为,则
D.若,,则
4.在对吸烟与患肺病这两个分类变量的独立性检验中,下列说法正确的是( )
(参考数据:)
① 若的观测值满足,我们有的把握认为吸烟与患肺病有关系;
② 若的观测值满足,那么在个吸烟的人中约有人患有肺病;
③ 从独立性检验可知,如果有的把握认为吸烟与患肺病有关系时,那么我们就认为:每个吸烟的人有的可能性会患肺病;
④ 从统计量中得知有的把握认为吸烟与患肺病有关系时,是指有的可能性使推断出现错误.
A.① B.①④ C.②③ D.①②③④
5.已知变量的成对样本数据的四个样本点,用最小二乘法得到回归方程 过点的直线方程为,给出下列4个命题:
①;
②;
③;
④点一定在直线上.
其中正确的命题的个数是( )
参考公式:,.
A.1个 B.2个 C.3个 D.4个
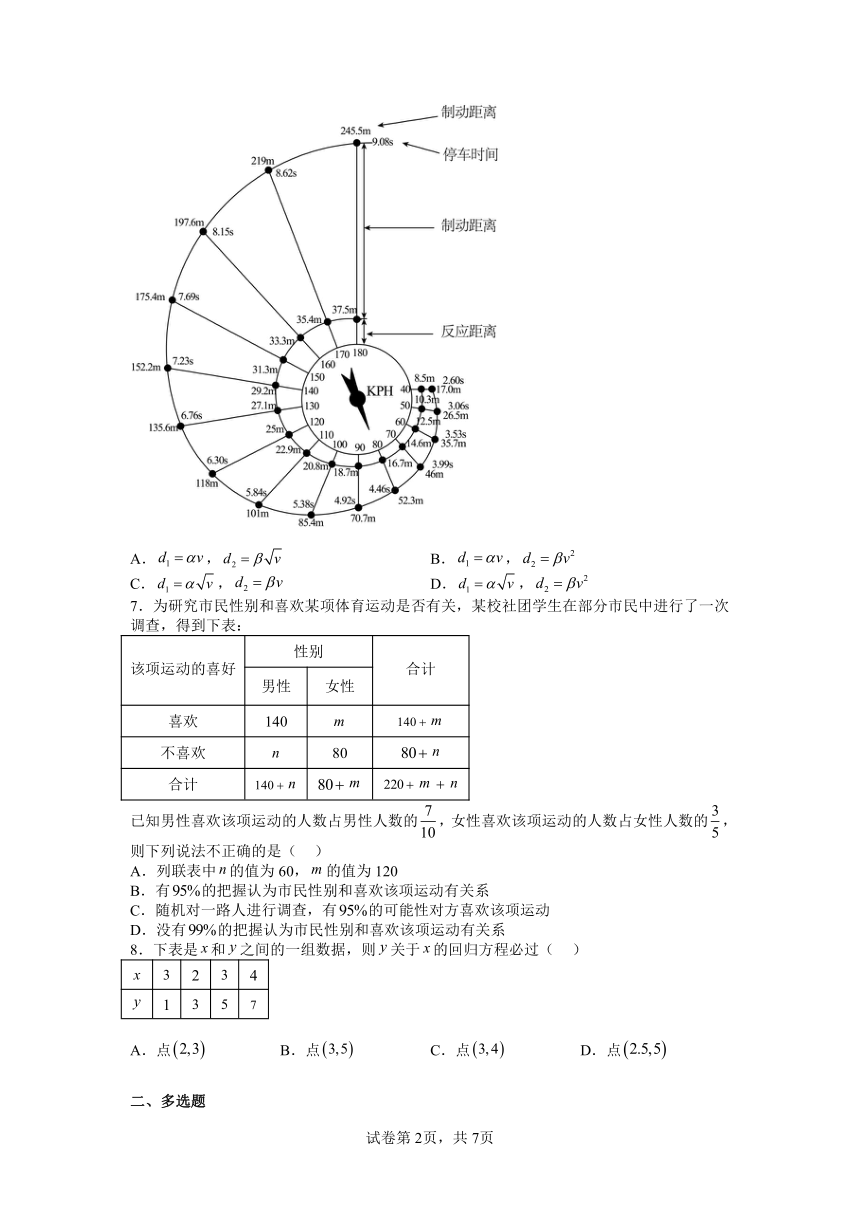
6.在研究急刹车的停车距离问题时,通常假定停车距离等于反应距离(,单位:m)与制动距离(,单位:m)之和.如图为某实验所测得的数据,其中“KPH”表示刹车时汽车的初速度(单位:km/h).根据实验数据可以推测,下面四组函数中最适合描述,与的函数关系的是( )
A., B.,
C., D.,
7.为研究市民性别和喜欢某项体育运动是否有关,某校社团学生在部分市民中进行了一次调查,得到下表:
该项运动的喜好 性别 合计
男性 女性
喜欢 140
不喜欢 80
合计
已知男性喜欢该项运动的人数占男性人数的,女性喜欢该项运动的人数占女性人数的,则下列说法不正确的是( )
A.列联表中的值为60,的值为120
B.有的把握认为市民性别和喜欢该项运动有关系
C.随机对一路人进行调查,有的可能性对方喜欢该项运动
D.没有的把握认为市民性别和喜欢该项运动有关系
8.下表是和之间的一组数据,则关于的回归方程必过( )
A.点 B.点 C.点 D.点
二、多选题
9.下列命题中正确的是( )
A.在回归分析中,成对样本数据的样本相关系数r的绝对值越大,成对样本数据的线性相关程度越强
B.在回归分析中,可用决定系数的值判断模型的拟合效果,越大,模型的拟合效果越好
C.比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越差
D.对分类变量X与Y,统计量的值越大,则判断“X与Y有关系”的把握程度越大
10.已知两个分类变量、,由它们的样本数据计算得到的观测值,的部分临界值表如下:
以下判断正确的是( )
A.在犯错误的概率不超过的前提下认为变量、有关系
B.在犯错误的概率不超过的前提下认为变量、没有关系
C.有的把握说变量、有关系
D.有的把握说变量、没有关系
11.下列命题正确的是( )
A.在回归分析中,相关指数越小,说明回归效果越好
B.已知,若根据2×2列联表得到的观测值为4.1,则有95%的把握认为两个分类变量有关
C.已知由一组样本数据(,2,,n)得到的回归直线方程为,且,则这组样本数据中一定有
D.若随机变量,则不论取何值,为定值
12.下列说法中正确的是( )
A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变
B.设有一个线性回归方程,变量增加1个单位时,平均增加5个单位
C.设具有相关关系的两个变量的相关系数为,则越接近于,和之间的线性相关程度越强
D.在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大
三、填空题
13.根据表中的数据,及观测值则在犯错误的概率不超过___________前提下,认为选择舞蹈与性别有关.
篮球 舞蹈 合计
男 13 7 20
女 2 8 10
合计 15 15 30
其中的参考数据:
0.05 0.025 0.010
3.841 5.024 6.635
14.已知回归方程,而试验得到一组数据是,则残差平方和是______.
15.某种产品的价格(单位:元/kg)与需求量(单位:kg)之间的对应数据如下表所示.
x 10 15 20 25 30
y 11 10 8 6 5
根据表中的数据可得回归直线方程,则以下正确的是________.
①相关系数;②;③若该产品价格为元/kg,则日需求量大约为kg;④第四个样本点对应的离差为.
16.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为__________分.(四舍五入取整数)
四、解答题
17.2021年因疫情的原因,我国电子商务蓬勃发展,管理部门推出了针对某网购平台的商品质量和服务质量的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品质量的满意率为0.55,对服务质量的满意率为0.7,其中对商品质量和服务质量都满意的交易为70次.
(1)根据已知条件完成下面的列联表,并回答能否有的把握认为“网购者对商品质量满意与对服务质量满意之间有关系”?
对服务质量满意 对服务质量不满意 合计
对商品质量满意 70
对商品质量不满意
合计 200
(2)若将频率视为概率,某人在该网购平台上进行的3次购物中,对商品质量和服务质量都满意和都不满意的概率各是多少?
附:.
0.15 0.10 0.05 0.025 0.010
k 2.072 2.706 3.841 5.024 6.635
18.近年来,随着网络时代的发展,线上销售成为了一种热门的发展趋势.为了了解产品A的线上销售对象对该产品的满意程度,研究人员随机抽取了部分客户作出调查,得到的数据如下表:
表示满意 表示不满意
男性 60 45
女性 30 45
(1)判断能否在犯错误的概率不超过0.025的前提下认为客户的满意程度与性别有关?
(2)根据以往数据,产品A的部分销售年份和线上销售总额之间呈现线性相关,数据统计如图所示,其中,,求关于的回归直线方程.
附:,,,其中.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
19.2021年5月11日上午10时,我国国新办举行新闻发布会,介绍第七次全国人口普查主要数据结果并答记者问.国家统计局局长宁吉旺在会上通报,全国人口共141178万人,与2010年的133972万人相比,增加了7206万人,增长;年平均增长率为,比2000年到2010年的年平均增长率下降个百分点.数据表明,我国人口10年来继续保持低速增长态势为了进一步优化生育政策,实施一对夫妻可以生育三个子女政策及配套支持措施.从2021年5月31日起统一实施全面三孩政策为了解适龄民众对放开生育三孩政策的态度,某市选取已生二胎的80后和90后作为调查对象,随机调查了100位,得到数据如表:
生三胎 不生三胎 合..计
80后 10 40 50
90后 30 20 50
合计 40 60 100
(1)以这100个人的样本数据估计该市的总体数据,且视频率为概率,若从该市已生二胎的90后公民中随机抽取3位,记其中生三胎的人数为,求随机变量的分布列,数学期望和方差;
(2)根据调查数据,是否有的把握认为“生三胎与年龄有关”,并说明理由.
参考公式:,其中.
参考数据:
20.在全面抗击新冠肺炎疫情这一特殊时期,学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取名学生进行跟踪问卷,其中每周线上学习数学时间不少于小时的有人,余下的人中,在检测考试中数学平均成绩不足分的占,统计成绩后得到如下列联表:
分数不少于分 分数不足分 合计
线上学习时间不少于小时
线上学习时间不足小时
合计
(1)请完成上面列联表;并判断是否有的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)按照分层抽样的方法,在上述样本中从分数不少于分和分数不足分的两组学生中抽取名学生,再从这名学生中随机抽取名学生,求抽取的两名学生分数都不足的概率.
(下面的临界值表供参考)
(参考公式,其中)
21.2023年5月10日长征七号火箭剑指苍穹,搭载天舟六号货运飞船为中国空间站运送补给物资,为中国空间站的航天员们长时间探索宇宙奥秘提供强有力的后援支持.某校部分学生十分关注中国空间站的发展,若将累计关注中国空间站发展的消息达到6次及以上者称为“航天达人”,未达到6次者称为“非航天达人”.现从该校随机抽取50人进行分析,得到数据如表所示:
航天达人 非航天达人 合计
男 20 26
女 14
合计
(1)补全2×2列联表,根据小概率值的独立性检验,能否认为“航天达人”与性别有关联
(2)现从抽取的“航天达人”中,按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取3人,记这3人中女“航天达人”的人数为X,求X的分布列和数学期望.
附:
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
22.某超市记录了某农副产品5个月内的月平均销售价格,得到的统计数据如下表:
月份x 1 2 3 4 5
月平均销售价格(单位:元/千克) 12 10.5 10 8.5 9
(1)若月平均销售价格y与月份x之间的回归直线方程为,求的值,并预测6月份该农副产品的月平均销售价格;
(2)求该农副产品5个月内的月平均销售价格这组数据的方差.
试卷第6页,共6页
一、单选题
1.某产品的宣传费用(万元)与销售额(万元)的统计数据如下表所示:
宣传费用(万元) 3 1 2 6
销售额(万元) 10 4 16
根据上表可得回归方程,则宣传费用为2万元时销售额为( )
A.4 B.5 C.6 D.7
2.已知变量与负相关,且由观测数据算得样本平均数,,则由该观测数据算得的线性回归方程可能是( )
A. B.
C. D.
3.下列说法正确的是( )
A.“A与B是互斥事件”是“A与B互为对立事件”的充分不必要条件
B.设具有线性相关关系的两个变量x,y的相关系数为r,则越接近于0,x,y之间线性相关程度越强
C.已知随机变量X的方差为,则
D.若,,则
4.在对吸烟与患肺病这两个分类变量的独立性检验中,下列说法正确的是( )
(参考数据:)
① 若的观测值满足,我们有的把握认为吸烟与患肺病有关系;
② 若的观测值满足,那么在个吸烟的人中约有人患有肺病;
③ 从独立性检验可知,如果有的把握认为吸烟与患肺病有关系时,那么我们就认为:每个吸烟的人有的可能性会患肺病;
④ 从统计量中得知有的把握认为吸烟与患肺病有关系时,是指有的可能性使推断出现错误.
A.① B.①④ C.②③ D.①②③④
5.已知变量的成对样本数据的四个样本点,用最小二乘法得到回归方程 过点的直线方程为,给出下列4个命题:
①;
②;
③;
④点一定在直线上.
其中正确的命题的个数是( )
参考公式:,.
A.1个 B.2个 C.3个 D.4个
6.在研究急刹车的停车距离问题时,通常假定停车距离等于反应距离(,单位:m)与制动距离(,单位:m)之和.如图为某实验所测得的数据,其中“KPH”表示刹车时汽车的初速度(单位:km/h).根据实验数据可以推测,下面四组函数中最适合描述,与的函数关系的是( )
A., B.,
C., D.,
7.为研究市民性别和喜欢某项体育运动是否有关,某校社团学生在部分市民中进行了一次调查,得到下表:
该项运动的喜好 性别 合计
男性 女性
喜欢 140
不喜欢 80
合计
已知男性喜欢该项运动的人数占男性人数的,女性喜欢该项运动的人数占女性人数的,则下列说法不正确的是( )
A.列联表中的值为60,的值为120
B.有的把握认为市民性别和喜欢该项运动有关系
C.随机对一路人进行调查,有的可能性对方喜欢该项运动
D.没有的把握认为市民性别和喜欢该项运动有关系
8.下表是和之间的一组数据,则关于的回归方程必过( )
A.点 B.点 C.点 D.点
二、多选题
9.下列命题中正确的是( )
A.在回归分析中,成对样本数据的样本相关系数r的绝对值越大,成对样本数据的线性相关程度越强
B.在回归分析中,可用决定系数的值判断模型的拟合效果,越大,模型的拟合效果越好
C.比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型拟合效果越差
D.对分类变量X与Y,统计量的值越大,则判断“X与Y有关系”的把握程度越大
10.已知两个分类变量、,由它们的样本数据计算得到的观测值,的部分临界值表如下:
以下判断正确的是( )
A.在犯错误的概率不超过的前提下认为变量、有关系
B.在犯错误的概率不超过的前提下认为变量、没有关系
C.有的把握说变量、有关系
D.有的把握说变量、没有关系
11.下列命题正确的是( )
A.在回归分析中,相关指数越小,说明回归效果越好
B.已知,若根据2×2列联表得到的观测值为4.1,则有95%的把握认为两个分类变量有关
C.已知由一组样本数据(,2,,n)得到的回归直线方程为,且,则这组样本数据中一定有
D.若随机变量,则不论取何值,为定值
12.下列说法中正确的是( )
A.将一组数据中的每一个数据都加上或减去同一个常数后,方差不变
B.设有一个线性回归方程,变量增加1个单位时,平均增加5个单位
C.设具有相关关系的两个变量的相关系数为,则越接近于,和之间的线性相关程度越强
D.在一个列联表中,由计算得的值,则的值越大,判断两个变量间有关联的把握就越大
三、填空题
13.根据表中的数据,及观测值则在犯错误的概率不超过___________前提下,认为选择舞蹈与性别有关.
篮球 舞蹈 合计
男 13 7 20
女 2 8 10
合计 15 15 30
其中的参考数据:
0.05 0.025 0.010
3.841 5.024 6.635
14.已知回归方程,而试验得到一组数据是,则残差平方和是______.
15.某种产品的价格(单位:元/kg)与需求量(单位:kg)之间的对应数据如下表所示.
x 10 15 20 25 30
y 11 10 8 6 5
根据表中的数据可得回归直线方程,则以下正确的是________.
①相关系数;②;③若该产品价格为元/kg,则日需求量大约为kg;④第四个样本点对应的离差为.
16.在一次考试中,5名学生的数学和物理成绩如下表(已知学生的数学和物理成绩具有线性相关关系):
学生的编号i 1 2 3 4 5
数学成绩x 80 75 70 65 60
物理成绩y 70 66 68 64 62
现已知其经验回归方程为=0.36x+,则根据此经验回归方程估计数学得90分的同学的物理成绩为__________分.(四舍五入取整数)
四、解答题
17.2021年因疫情的原因,我国电子商务蓬勃发展,管理部门推出了针对某网购平台的商品质量和服务质量的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品质量的满意率为0.55,对服务质量的满意率为0.7,其中对商品质量和服务质量都满意的交易为70次.
(1)根据已知条件完成下面的列联表,并回答能否有的把握认为“网购者对商品质量满意与对服务质量满意之间有关系”?
对服务质量满意 对服务质量不满意 合计
对商品质量满意 70
对商品质量不满意
合计 200
(2)若将频率视为概率,某人在该网购平台上进行的3次购物中,对商品质量和服务质量都满意和都不满意的概率各是多少?
附:.
0.15 0.10 0.05 0.025 0.010
k 2.072 2.706 3.841 5.024 6.635
18.近年来,随着网络时代的发展,线上销售成为了一种热门的发展趋势.为了了解产品A的线上销售对象对该产品的满意程度,研究人员随机抽取了部分客户作出调查,得到的数据如下表:
表示满意 表示不满意
男性 60 45
女性 30 45
(1)判断能否在犯错误的概率不超过0.025的前提下认为客户的满意程度与性别有关?
(2)根据以往数据,产品A的部分销售年份和线上销售总额之间呈现线性相关,数据统计如图所示,其中,,求关于的回归直线方程.
附:,,,其中.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
19.2021年5月11日上午10时,我国国新办举行新闻发布会,介绍第七次全国人口普查主要数据结果并答记者问.国家统计局局长宁吉旺在会上通报,全国人口共141178万人,与2010年的133972万人相比,增加了7206万人,增长;年平均增长率为,比2000年到2010年的年平均增长率下降个百分点.数据表明,我国人口10年来继续保持低速增长态势为了进一步优化生育政策,实施一对夫妻可以生育三个子女政策及配套支持措施.从2021年5月31日起统一实施全面三孩政策为了解适龄民众对放开生育三孩政策的态度,某市选取已生二胎的80后和90后作为调查对象,随机调查了100位,得到数据如表:
生三胎 不生三胎 合..计
80后 10 40 50
90后 30 20 50
合计 40 60 100
(1)以这100个人的样本数据估计该市的总体数据,且视频率为概率,若从该市已生二胎的90后公民中随机抽取3位,记其中生三胎的人数为,求随机变量的分布列,数学期望和方差;
(2)根据调查数据,是否有的把握认为“生三胎与年龄有关”,并说明理由.
参考公式:,其中.
参考数据:
20.在全面抗击新冠肺炎疫情这一特殊时期,学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取名学生进行跟踪问卷,其中每周线上学习数学时间不少于小时的有人,余下的人中,在检测考试中数学平均成绩不足分的占,统计成绩后得到如下列联表:
分数不少于分 分数不足分 合计
线上学习时间不少于小时
线上学习时间不足小时
合计
(1)请完成上面列联表;并判断是否有的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)按照分层抽样的方法,在上述样本中从分数不少于分和分数不足分的两组学生中抽取名学生,再从这名学生中随机抽取名学生,求抽取的两名学生分数都不足的概率.
(下面的临界值表供参考)
(参考公式,其中)
21.2023年5月10日长征七号火箭剑指苍穹,搭载天舟六号货运飞船为中国空间站运送补给物资,为中国空间站的航天员们长时间探索宇宙奥秘提供强有力的后援支持.某校部分学生十分关注中国空间站的发展,若将累计关注中国空间站发展的消息达到6次及以上者称为“航天达人”,未达到6次者称为“非航天达人”.现从该校随机抽取50人进行分析,得到数据如表所示:
航天达人 非航天达人 合计
男 20 26
女 14
合计
(1)补全2×2列联表,根据小概率值的独立性检验,能否认为“航天达人”与性别有关联
(2)现从抽取的“航天达人”中,按性别采用分层抽样的方法抽取6人,然后从这6人中随机抽取3人,记这3人中女“航天达人”的人数为X,求X的分布列和数学期望.
附:
0.100 0.050 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
22.某超市记录了某农副产品5个月内的月平均销售价格,得到的统计数据如下表:
月份x 1 2 3 4 5
月平均销售价格(单位:元/千克) 12 10.5 10 8.5 9
(1)若月平均销售价格y与月份x之间的回归直线方程为,求的值,并预测6月份该农副产品的月平均销售价格;
(2)求该农副产品5个月内的月平均销售价格这组数据的方差.
试卷第6页,共6页
