北师大版七年级上册4.3 角同步练习(含解析)
文档属性
| 名称 | 北师大版七年级上册4.3 角同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览




文档简介
《角》同步同步练习
(
选择题
)
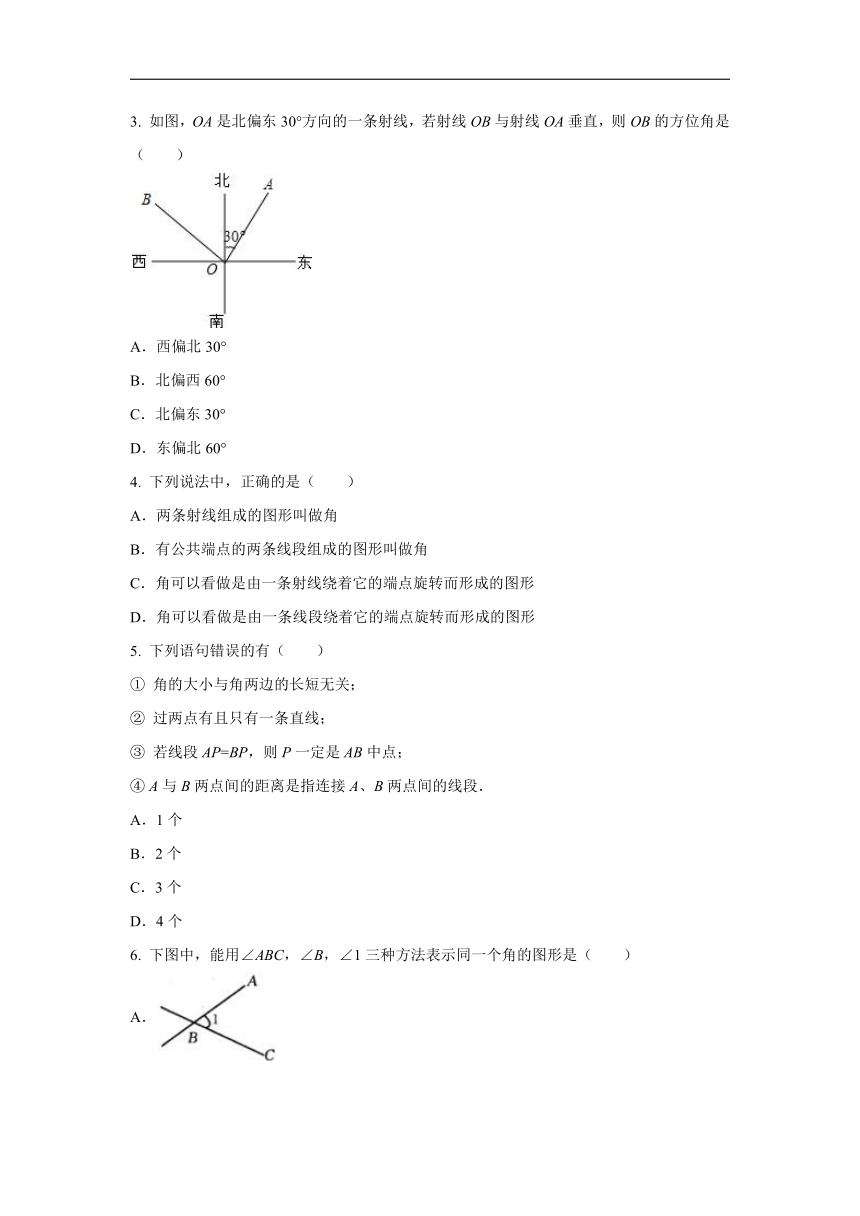
1. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )
A.
B.
C.
D.
2. 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
A.70°
B.20°
C.35°
D.110°
3. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是( )
A.西偏北30°
B.北偏西60°
C.北偏东30°
D.东偏北60°
4. 下列说法中,正确的是( )
A.两条射线组成的图形叫做角
B.有公共端点的两条线段组成的图形叫做角
C.角可以看做是由一条射线绕着它的端点旋转而形成的图形
D.角可以看做是由一条线段绕着它的端点旋转而形成的图形
5. 下列语句错误的有( )
① 角的大小与角两边的长短无关;
② 过两点有且只有一条直线;
③ 若线段AP=BP,则P一定是AB中点;
④ A与B两点间的距离是指连接A、B两点间的线段.
A.1个
B.2个
C.3个
D.4个
6. 下图中,能用∠ABC,∠B,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
7. 如图所示,下列表示角的方法错误的是( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
8. 在时刻8:30时,时钟上的时针与分针之间的所成的夹角是( )
A.60°
B.70°
C.75°
D.85°
9. 已知点A在点B的北偏东40°方向,则点B在点A的( )
A.北偏东50°方向
B.南偏西50°方向
C.南偏东40°方向
D.南偏西40°方向
10. 轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
A.南偏西32°
B.南偏东58°
C.南偏西58°
D.南偏东32°
11. 如图,点A位于点O的( )
A.南偏西25°方向上
B.北偏西65°方向上
C.南偏东65°方向上
D.南偏西65°方向上
12. 下图中能用一个字母表示的角( )
A.三个
B.四个
C.五个
D.没有
13. 下列说法正确的是( )
A.角的边越长,角度就越大
B.周角就是一条射线
C.一条直线可以看成平角
D.平角的两边可以构成一条直线
14. 如图,下列表示角的方法,错误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC不可用∠O来表示
C.图中共有三个角:∠AOB、∠AOC、∠BOC
D.∠β表示的是∠AOC
15. 在9点30分时,时针上的时针与分针之间的夹角为( )
A.85度
B.90度
C.70度
D.60度
(
填空题
)
16. 如图是一个时钟的钟面,下午1点30分,时钟的分针与时针所夹的角等于______°
.
17. 已知小岛A位于基地O的东南方向,货船B位于基地O的北偏东50°方向,那么∠AOB的度数等于______.
18. 从中午12时整到下午3时整,钟表时针所转过的角的度数是______.
19. C岛在B岛的北偏西48°方向,∠ACB等于95°,则C岛在A岛的______方向.
20. 如图,一艘轮船在A处看见巡逻艇M在其北偏东65°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东15°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=______.
(
解答
题
)
21. 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.
(1)B地修公路的走向是南偏西多少度?
(2)若公路AB长12千米,另一条公路BC长6千米,且BC的走向是北偏西44°,试求A到公路BC的距离?
22. 如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点在C处的西北方向,求∠ABC及∠BCA的度数.
23. 在AB两地之间要修一条笔直的公路,从A地测得公路的走向是南偏西56°,此工程由甲乙丙三支施工队伍共同建设.已知甲单独做要10天完成,乙单独做要12天完成,丙单独做要15天完成.甲、丙先合做了3天后,甲因事离去,由乙和丙完成剩下工作,那么还需要几天才能完成?并画出这条公路的简单示意图.
24. 如图所示,从一点O出发引射线OA、OB、OC、OD,请你数一数图中有多少个角,并把它们表示出来.
25. 如图所示,从一点O出发,引两条射线可以得到一个角,引三条射线可以得到三个角,引四条射线可以得到六个角,引五条射线可以得到十个角,如果从一点出发引n(n为大于等于2的整数)条射线,则会得到多少个角?如果n=8时,检验你所得的结论是否正确.
答案与解析
(
选择题
)
1. 答案:D
解析:根据岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,故D符合.
故选:D.
分析:根据方向角的定义,即可解答.
2. 答案:A
解析:如图,连接AB,
∵两正北方向平行,
∴∠ CAB+∠CBA=180°-45°-25°=110°,
∴∠ ACB=180°-110°=70°.
故选:A.
分析:根据两直线平行,同旁内角相等求得∠C的度数即可.
3. 答案:B
解析:∵射线OB与射线OA垂直,
∴∠AOB=90°,
∴∠1=90°-30°=60°,
故射线OB的方位角是北偏西60°,
故选B.
分析:根据垂直,可得∠AOB的度数,根据角的和差,可得答案.
4. 答案:C
解析:A. 有公共端点的两条射线组成的图形叫做角,故错误;
B. 根据A可得B错误;
C. 角可以看做是由一条射线绕着它的端点旋转而形成的图形,正确;
D. 据C可得D错误.
故选C.
分析:根据角的动态定义一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角.所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
5. 答案:B
解析:①角的大小与角两边的长短无关,正确;
②过两点有且只有一条直线,正确;
③若线段AP=BP,则P一定是AB中点;错误,点P可能不在AB上;
④A与B两点间的距离是指连接A、B两点间的线段;错误,因为A与B两点间的距离是指连接A、B两点间的线段的长度.
故选B
分析:根据直线、线段以及射线的概念来解答本题即可.
6. 答案:D
解析:A. 顶点B处有四个角,不能用∠B表示,错误;
B. 顶点B处有二个角,不能用∠B表示,错误;
C. 顶点B处有三个角,不能用∠B表示,错误;
D. 顶点B处有一个角,能同时用∠ABC,∠B,∠1表示,正确.
故选D.
分析:当角的顶点处只有一个角时,可以用一个大写字母表示这个角,也可以用三个大写字母表示这个角.
7. 答案:D
解析:A. ∠1与∠AOB表示同一个角,正确,故本选项错误;
B. ∠β表示的是∠BOC,正确,故本选项错误;
C. 图中共有三个角:∠AOB,∠AOC,∠BOC,正确,故本选项错误;
D. ∠AOC不能用∠O表示,错误,故本选项正确;
故选D.
分析:根据角的表示方法表示各个角,再判断即可.
8. 答案:C
解析:8点30分,时针和分针中间相差2. 5个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴8点30分分针与时针的夹角是2. 5×30°=75°,
故选C.
分析:利用钟表表盘的特征解答即可.
9. 答案:D
解析:如图,
则点B在点A的南偏西40度,
故选D.
分析:此题是对方向角的考查,若点A在点B的北偏东40度,要求点B在点A的方向,则以点A为原点建立直角坐标系即可求解.
10. 答案:D
解析:由图可知,AB方向相反,从小岛A同时观测轮船B的方向是南偏东32°,
故选:D.
分析:方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.根据定义就可以解决.
11. 答案:B
解析:∵OA和正西方向的夹角是25°,
∴OA与正北方向的夹角为65°,
∴位于点O的北偏西65°的方向上.
故选B.
分析:根据方位角的概念,结合上北下南左西右东的规定进行判断.
12. 答案:A
解析:∵只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,
∴图中能用一个字母表示的角有三个:
∠A、∠B、∠C.
故选:A.
分析:只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角,据此判断出图中能用一个字母表示的角有几个即可.
13. 答案:D
解析:A. 角的大小与边长无关,故错误;
B. 周角的特点是两条边重合成射线,但不能说成周角是一条射线,故错误;
C. 平角的特点是两条边成一条直线,不能说直线是平角,故错误;
D. 平角的两边构成一条直线,正确,
故选D.
分析:利用角的定义分别判断后即可确定正确的选项.
14. 答案:D
解析:∵∠1与∠AOB表示同一个角,
∴选项A正确.
∵只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,
∴∠AOC不能∠O来表示,
∴选项B正确.
∵图中共有三个角:∠AOB、∠AOC、∠BOC,
∴选项C正确.
∵∠β表示的是∠BOC,
∴选项D错误.
故选:D.
分析:A:根据角的表示方法判断即可.
B:只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,所以∠AOC不能∠O来表示,据此判断即可.
C:根据角的概念,判断出图中一共有多少个角即可.
D:根据角的表示方法判断即可.
15. 答案:B
解析:9点30分,时针和分针中间相差3个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴9点30分分针与时针的夹角是3×30°=90°.
故选:B.
分析:根据钟表上12个数字,每相邻两个数字之间的夹角为30°计算得到答案.
(
填空题
)
16. 解析:30°×(4+)=30°×=135°,
故答案为:135.
分析:根据钟面平均分成12份,可得每份30°,根据每份的度数乘以时针与分针相距的份数,可得答案.
17. 答案:85°
解析:如图:∵∠2=50°,
∴∠3=40°,
∵∠1=45°,
∴∠AOB=∠1+∠3=45°+40°=85°,
故答案为:85°.
分析:根据方位角的概念,画图正确表示出A,B的方位,易得结果.
18. 答案:90°
解析:时针经过3个小时,那么它转过的角度是30°×3=90°.
故答案为:90°.
分析:利用钟表表盘的特征解答.时针每小时走30°.
19. 答案:北偏东47°
解析:作CF∥AD,则AD∥CF∥BE.
∵AD∥CF,
∴∠ACF=∠DAC,
同理∠BCF=∠CBE=48°,
∴∠DAC=∠ACB-∠BCF=95°-48°=47°,
则北偏东47°方向.
故答案是:北偏东47°.
分析:作CF∥AD,则AD∥CF∥BE,根据平行线的性质可得∠ACF=∠DAC,∠BCF=∠CBE,据此即可求得∠DAC的度数,从而求解.
20. 答案:50°
解析:从图中我们可以发现∠AMB=180°-(90°+15°)-(90°-65°)=50°,
故答案为:50°.
分析:将轮船航行的实际问题转化为方向角的问题解答.
(
解答
题
)
21. (1)答案:南偏西46°;
由两地南北方向平行,根据内错角相等,可知B地所修公路的走向是南偏西46°;
(2)答案:12千米.
∵∠ ABC=180°-∠ABG-∠EBC=180°-46°-44°=90°,
∴AB⊥BC,
∴A地到公路BC的距离是AB=12千米.
分析:根据方位角的概念,图中给出的信息,再根据已知转向的角度求解.
22. 答案: 45°|50°.
∵∠DBA=40°,∠DBC=85°,DB∥CE,
∴∠ECB=180°-85°=95°,∠ABC=85°-40°=45°,
∵∠ECA=45°,
∴∠BCA=95°-45°=50°.
分析:根据方位角的概念,图中给出的信息,结合平行线的性质求解即可.
23. 答案:天;如图,
设由乙和丙完成剩下工作,那么还需要x天才能完成,
根据题意得:,
解得:.
∴由乙和丙完成剩下工作,那么还需要天才能完成.
分析:先建立方位图,再设由乙和丙完成剩下工作,那么还需要x天才能完成,根据题意列出方程,即可解答.
24. 答案:共6个角,有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD,共6个角.
分析:根据角的概念(有公共端点的两条射线组成的图形叫角)写出即可,注意不要漏角啊.
25. 答案:当n=2时,角的个数为1;
当n=3时,角的个数为1+2=3;
当n=4时,角的个数为1+2+3=6;
当n=5时,角的个数为1+2+3+4=10;
当射线的条数为n时,角的个数为1+2+3+4+…+(n-2)+(n-1)=(n-1)n,
当n=8时,×(8-1)×8=28.所以n条射线可组成(n-1) n个角,这个结论也是正确的.
分析:根据图形分别n的值与角的个数的关系,进而得出规律求出即可.
(
选择题
)
1. 已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,符合条件的示意图是( )
A.
B.
C.
D.
2. 如图,C岛在A岛的北偏东45°方向,C岛在B岛的北偏西25°方向,则从C岛看A、B两岛的视角∠ACB的度数是( )
A.70°
B.20°
C.35°
D.110°
3. 如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是( )
A.西偏北30°
B.北偏西60°
C.北偏东30°
D.东偏北60°
4. 下列说法中,正确的是( )
A.两条射线组成的图形叫做角
B.有公共端点的两条线段组成的图形叫做角
C.角可以看做是由一条射线绕着它的端点旋转而形成的图形
D.角可以看做是由一条线段绕着它的端点旋转而形成的图形
5. 下列语句错误的有( )
① 角的大小与角两边的长短无关;
② 过两点有且只有一条直线;
③ 若线段AP=BP,则P一定是AB中点;
④ A与B两点间的距离是指连接A、B两点间的线段.
A.1个
B.2个
C.3个
D.4个
6. 下图中,能用∠ABC,∠B,∠1三种方法表示同一个角的图形是( )
A.
B.
C.
D.
7. 如图所示,下列表示角的方法错误的是( )
A.∠1与∠AOB表示同一个角
B.∠β表示的是∠BOC
C.图中共有三个角:∠AOB,∠AOC,∠BOC
D.∠AOC也可用∠O来表示
8. 在时刻8:30时,时钟上的时针与分针之间的所成的夹角是( )
A.60°
B.70°
C.75°
D.85°
9. 已知点A在点B的北偏东40°方向,则点B在点A的( )
A.北偏东50°方向
B.南偏西50°方向
C.南偏东40°方向
D.南偏西40°方向
10. 轮船航行到B处观测小岛A的方向是北偏西32°,那么小岛A观测到轮船B的方向是( )
A.南偏西32°
B.南偏东58°
C.南偏西58°
D.南偏东32°
11. 如图,点A位于点O的( )
A.南偏西25°方向上
B.北偏西65°方向上
C.南偏东65°方向上
D.南偏西65°方向上
12. 下图中能用一个字母表示的角( )
A.三个
B.四个
C.五个
D.没有
13. 下列说法正确的是( )
A.角的边越长,角度就越大
B.周角就是一条射线
C.一条直线可以看成平角
D.平角的两边可以构成一条直线
14. 如图,下列表示角的方法,错误的是( )
A.∠1与∠AOB表示同一个角
B.∠AOC不可用∠O来表示
C.图中共有三个角:∠AOB、∠AOC、∠BOC
D.∠β表示的是∠AOC
15. 在9点30分时,时针上的时针与分针之间的夹角为( )
A.85度
B.90度
C.70度
D.60度
(
填空题
)
16. 如图是一个时钟的钟面,下午1点30分,时钟的分针与时针所夹的角等于______°
.
17. 已知小岛A位于基地O的东南方向,货船B位于基地O的北偏东50°方向,那么∠AOB的度数等于______.
18. 从中午12时整到下午3时整,钟表时针所转过的角的度数是______.
19. C岛在B岛的北偏西48°方向,∠ACB等于95°,则C岛在A岛的______方向.
20. 如图,一艘轮船在A处看见巡逻艇M在其北偏东65°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东15°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=______.
(
解答
题
)
21. 如图,在A、B两处之间要修一条笔直的公路,从A地测得公路走向是北偏东46°,A、B两地同时开工,若干天后公路准确接通.
(1)B地修公路的走向是南偏西多少度?
(2)若公路AB长12千米,另一条公路BC长6千米,且BC的走向是北偏西44°,试求A到公路BC的距离?
22. 如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点在C处的西北方向,求∠ABC及∠BCA的度数.
23. 在AB两地之间要修一条笔直的公路,从A地测得公路的走向是南偏西56°,此工程由甲乙丙三支施工队伍共同建设.已知甲单独做要10天完成,乙单独做要12天完成,丙单独做要15天完成.甲、丙先合做了3天后,甲因事离去,由乙和丙完成剩下工作,那么还需要几天才能完成?并画出这条公路的简单示意图.
24. 如图所示,从一点O出发引射线OA、OB、OC、OD,请你数一数图中有多少个角,并把它们表示出来.
25. 如图所示,从一点O出发,引两条射线可以得到一个角,引三条射线可以得到三个角,引四条射线可以得到六个角,引五条射线可以得到十个角,如果从一点出发引n(n为大于等于2的整数)条射线,则会得到多少个角?如果n=8时,检验你所得的结论是否正确.
答案与解析
(
选择题
)
1. 答案:D
解析:根据岛P,Q分别测得船R位于南偏东30°和南偏西45°方向上,故D符合.
故选:D.
分析:根据方向角的定义,即可解答.
2. 答案:A
解析:如图,连接AB,
∵两正北方向平行,
∴∠ CAB+∠CBA=180°-45°-25°=110°,
∴∠ ACB=180°-110°=70°.
故选:A.
分析:根据两直线平行,同旁内角相等求得∠C的度数即可.
3. 答案:B
解析:∵射线OB与射线OA垂直,
∴∠AOB=90°,
∴∠1=90°-30°=60°,
故射线OB的方位角是北偏西60°,
故选B.
分析:根据垂直,可得∠AOB的度数,根据角的和差,可得答案.
4. 答案:C
解析:A. 有公共端点的两条射线组成的图形叫做角,故错误;
B. 根据A可得B错误;
C. 角可以看做是由一条射线绕着它的端点旋转而形成的图形,正确;
D. 据C可得D错误.
故选C.
分析:根据角的动态定义一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形叫做角.所旋转射线的端点叫做角的顶点,开始位置的射线叫做角的始边,终止位置的射线叫做角的终边.
5. 答案:B
解析:①角的大小与角两边的长短无关,正确;
②过两点有且只有一条直线,正确;
③若线段AP=BP,则P一定是AB中点;错误,点P可能不在AB上;
④A与B两点间的距离是指连接A、B两点间的线段;错误,因为A与B两点间的距离是指连接A、B两点间的线段的长度.
故选B
分析:根据直线、线段以及射线的概念来解答本题即可.
6. 答案:D
解析:A. 顶点B处有四个角,不能用∠B表示,错误;
B. 顶点B处有二个角,不能用∠B表示,错误;
C. 顶点B处有三个角,不能用∠B表示,错误;
D. 顶点B处有一个角,能同时用∠ABC,∠B,∠1表示,正确.
故选D.
分析:当角的顶点处只有一个角时,可以用一个大写字母表示这个角,也可以用三个大写字母表示这个角.
7. 答案:D
解析:A. ∠1与∠AOB表示同一个角,正确,故本选项错误;
B. ∠β表示的是∠BOC,正确,故本选项错误;
C. 图中共有三个角:∠AOB,∠AOC,∠BOC,正确,故本选项错误;
D. ∠AOC不能用∠O表示,错误,故本选项正确;
故选D.
分析:根据角的表示方法表示各个角,再判断即可.
8. 答案:C
解析:8点30分,时针和分针中间相差2. 5个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴8点30分分针与时针的夹角是2. 5×30°=75°,
故选C.
分析:利用钟表表盘的特征解答即可.
9. 答案:D
解析:如图,
则点B在点A的南偏西40度,
故选D.
分析:此题是对方向角的考查,若点A在点B的北偏东40度,要求点B在点A的方向,则以点A为原点建立直角坐标系即可求解.
10. 答案:D
解析:由图可知,AB方向相反,从小岛A同时观测轮船B的方向是南偏东32°,
故选:D.
分析:方向角一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.根据定义就可以解决.
11. 答案:B
解析:∵OA和正西方向的夹角是25°,
∴OA与正北方向的夹角为65°,
∴位于点O的北偏西65°的方向上.
故选B.
分析:根据方位角的概念,结合上北下南左西右东的规定进行判断.
12. 答案:A
解析:∵只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,
∴图中能用一个字母表示的角有三个:
∠A、∠B、∠C.
故选:A.
分析:只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角,据此判断出图中能用一个字母表示的角有几个即可.
13. 答案:D
解析:A. 角的大小与边长无关,故错误;
B. 周角的特点是两条边重合成射线,但不能说成周角是一条射线,故错误;
C. 平角的特点是两条边成一条直线,不能说直线是平角,故错误;
D. 平角的两边构成一条直线,正确,
故选D.
分析:利用角的定义分别判断后即可确定正确的选项.
14. 答案:D
解析:∵∠1与∠AOB表示同一个角,
∴选项A正确.
∵只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,
∴∠AOC不能∠O来表示,
∴选项B正确.
∵图中共有三个角:∠AOB、∠AOC、∠BOC,
∴选项C正确.
∵∠β表示的是∠BOC,
∴选项D错误.
故选:D.
分析:A:根据角的表示方法判断即可.
B:只有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,所以∠AOC不能∠O来表示,据此判断即可.
C:根据角的概念,判断出图中一共有多少个角即可.
D:根据角的表示方法判断即可.
15. 答案:B
解析:9点30分,时针和分针中间相差3个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴9点30分分针与时针的夹角是3×30°=90°.
故选:B.
分析:根据钟表上12个数字,每相邻两个数字之间的夹角为30°计算得到答案.
(
填空题
)
16. 解析:30°×(4+)=30°×=135°,
故答案为:135.
分析:根据钟面平均分成12份,可得每份30°,根据每份的度数乘以时针与分针相距的份数,可得答案.
17. 答案:85°
解析:如图:∵∠2=50°,
∴∠3=40°,
∵∠1=45°,
∴∠AOB=∠1+∠3=45°+40°=85°,
故答案为:85°.
分析:根据方位角的概念,画图正确表示出A,B的方位,易得结果.
18. 答案:90°
解析:时针经过3个小时,那么它转过的角度是30°×3=90°.
故答案为:90°.
分析:利用钟表表盘的特征解答.时针每小时走30°.
19. 答案:北偏东47°
解析:作CF∥AD,则AD∥CF∥BE.
∵AD∥CF,
∴∠ACF=∠DAC,
同理∠BCF=∠CBE=48°,
∴∠DAC=∠ACB-∠BCF=95°-48°=47°,
则北偏东47°方向.
故答案是:北偏东47°.
分析:作CF∥AD,则AD∥CF∥BE,根据平行线的性质可得∠ACF=∠DAC,∠BCF=∠CBE,据此即可求得∠DAC的度数,从而求解.
20. 答案:50°
解析:从图中我们可以发现∠AMB=180°-(90°+15°)-(90°-65°)=50°,
故答案为:50°.
分析:将轮船航行的实际问题转化为方向角的问题解答.
(
解答
题
)
21. (1)答案:南偏西46°;
由两地南北方向平行,根据内错角相等,可知B地所修公路的走向是南偏西46°;
(2)答案:12千米.
∵∠ ABC=180°-∠ABG-∠EBC=180°-46°-44°=90°,
∴AB⊥BC,
∴A地到公路BC的距离是AB=12千米.
分析:根据方位角的概念,图中给出的信息,再根据已知转向的角度求解.
22. 答案: 45°|50°.
∵∠DBA=40°,∠DBC=85°,DB∥CE,
∴∠ECB=180°-85°=95°,∠ABC=85°-40°=45°,
∵∠ECA=45°,
∴∠BCA=95°-45°=50°.
分析:根据方位角的概念,图中给出的信息,结合平行线的性质求解即可.
23. 答案:天;如图,
设由乙和丙完成剩下工作,那么还需要x天才能完成,
根据题意得:,
解得:.
∴由乙和丙完成剩下工作,那么还需要天才能完成.
分析:先建立方位图,再设由乙和丙完成剩下工作,那么还需要x天才能完成,根据题意列出方程,即可解答.
24. 答案:共6个角,有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD,共6个角.
分析:根据角的概念(有公共端点的两条射线组成的图形叫角)写出即可,注意不要漏角啊.
25. 答案:当n=2时,角的个数为1;
当n=3时,角的个数为1+2=3;
当n=4时,角的个数为1+2+3=6;
当n=5时,角的个数为1+2+3+4=10;
当射线的条数为n时,角的个数为1+2+3+4+…+(n-2)+(n-1)=(n-1)n,
当n=8时,×(8-1)×8=28.所以n条射线可组成(n-1) n个角,这个结论也是正确的.
分析:根据图形分别n的值与角的个数的关系,进而得出规律求出即可.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
