18.5 实践与探索-课题学习[下学期]
文档属性
| 名称 | 18.5 实践与探索-课题学习[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 181.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-06 09:50:00 | ||
图片预览



文档简介
课件13张PPT。课题:
怎样测量旗杆的高度 ?
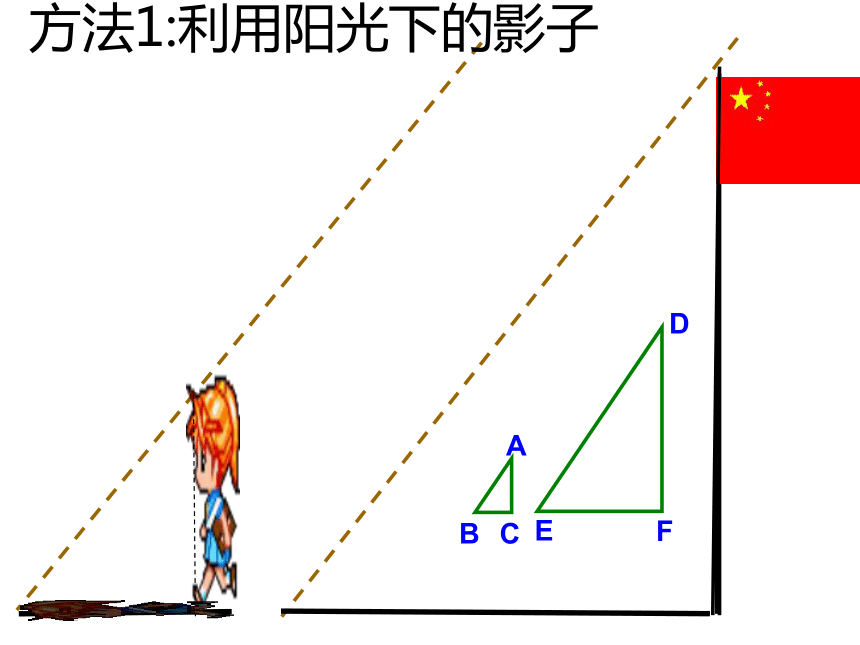
方法1:利用阳光下的影子 例1、小敏测得2m高的标杆在太阳光下的影长为1.2m,同时又测得一颗树的影长为12m,请你计算出这棵树的高度。解:如图所示:
AC表示标杆,BC表示标杆的影长,DF表示树高,由题意知:
△ ABC∽ △ DEF
∴
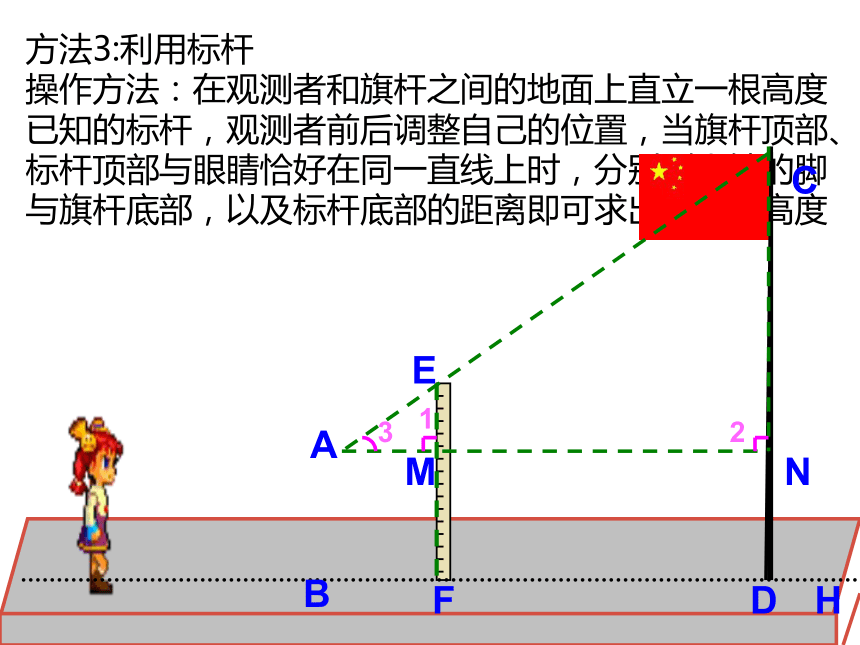
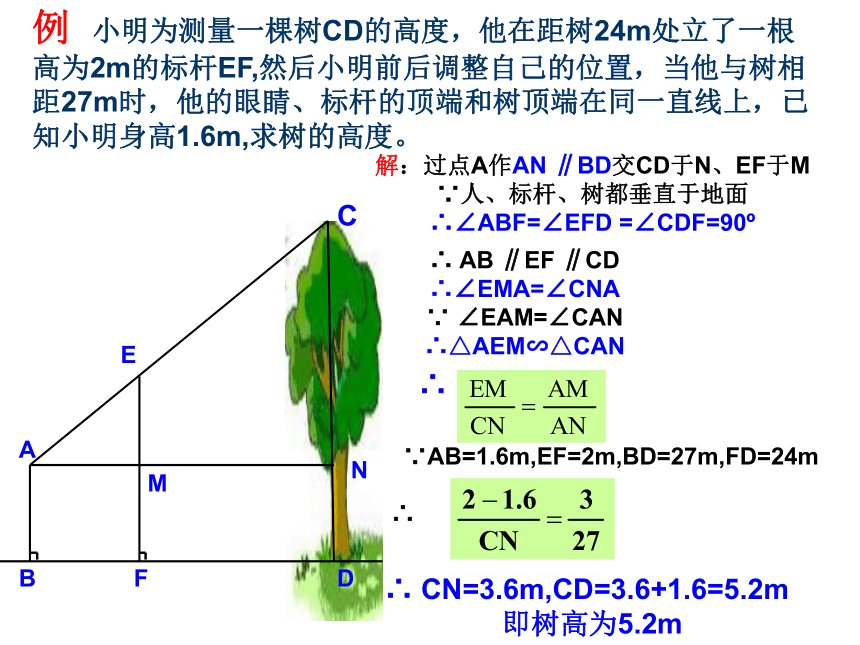
∴ DF=20∴ 所以树的高度为20米方法2:利用仰角或测角仪方法3:利用标杆 操作方法:在观测者和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,分别测出她的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度 例 小明为测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明身高1.6m,求树的高度。解:过点A作AN ∥BD交CD于N、EF于M
∵人、标杆、树都垂直于地面
∴∠ABF=∠EFD =∠CDF=90o∴ AB ∥EF ∥CD
∴∠EMA=∠CNA
∵ ∠EAM=∠CAN
∴△AEM∽△CAN∴ CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m方法4:利用镜子例2、如图,在距离树高AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶。若人眼距地面1.4米,求树高。 解:由题意知:BE=18米、DE=2.1米、CD=1.4米,且△ ABE∽ △ CDE
AB= 12 所以树高为12米∴∴∴34。如果站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34。 ,并且目高AD为1米。现在请你按1:500的比例将ΔABC 画在纸上,并记为ΔA’B’C’ ,用刻度直尺量出纸上B’C’ 的长度,便可以算出旗杆的实际高度。ABDECA'C'B'方法5:利用画图 45。如果站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为45。 ,并且目高AD为1米。ABDECA'C'B'拓展训练 某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.作业: 课本122页课题学习,写出实习报告.
怎样测量旗杆的高度 ?
方法1:利用阳光下的影子 例1、小敏测得2m高的标杆在太阳光下的影长为1.2m,同时又测得一颗树的影长为12m,请你计算出这棵树的高度。解:如图所示:
AC表示标杆,BC表示标杆的影长,DF表示树高,由题意知:
△ ABC∽ △ DEF
∴
∴ DF=20∴ 所以树的高度为20米方法2:利用仰角或测角仪方法3:利用标杆 操作方法:在观测者和旗杆之间的地面上直立一根高度已知的标杆,观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,分别测出她的脚与旗杆底部,以及标杆底部的距离即可求出旗杆的高度 例 小明为测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明身高1.6m,求树的高度。解:过点A作AN ∥BD交CD于N、EF于M
∵人、标杆、树都垂直于地面
∴∠ABF=∠EFD =∠CDF=90o∴ AB ∥EF ∥CD
∴∠EMA=∠CNA
∵ ∠EAM=∠CAN
∴△AEM∽△CAN∴ CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m方法4:利用镜子例2、如图,在距离树高AB 18米的地面上平放着一面镜子E,人退后到距镜子2.1米的D处,在镜子里恰看见树顶。若人眼距地面1.4米,求树高。 解:由题意知:BE=18米、DE=2.1米、CD=1.4米,且△ ABE∽ △ CDE
AB= 12 所以树高为12米∴∴∴34。如果站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为34。 ,并且目高AD为1米。现在请你按1:500的比例将ΔABC 画在纸上,并记为ΔA’B’C’ ,用刻度直尺量出纸上B’C’ 的长度,便可以算出旗杆的实际高度。ABDECA'C'B'方法5:利用画图 45。如果站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC为45。 ,并且目高AD为1米。ABDECA'C'B'拓展训练 某同学想测旗杆的高度,他在某一时刻测得1m长的竹竿竖直时的影长为1.5m,同一时刻测量旗杆影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为9m,留在墙上的影长为2m,求旗杆的高度。数学源于生活,又反过来服务于生活.如果你无愧于数学,那数学就可以助你到达胜利的彼岸.作业: 课本122页课题学习,写出实习报告.
