2022-2023学年人教版(五四制)七年级数学下册《第18章全等三角形》期末综合复习题(含解析)
文档属性
| 名称 | 2022-2023学年人教版(五四制)七年级数学下册《第18章全等三角形》期末综合复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 134.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览


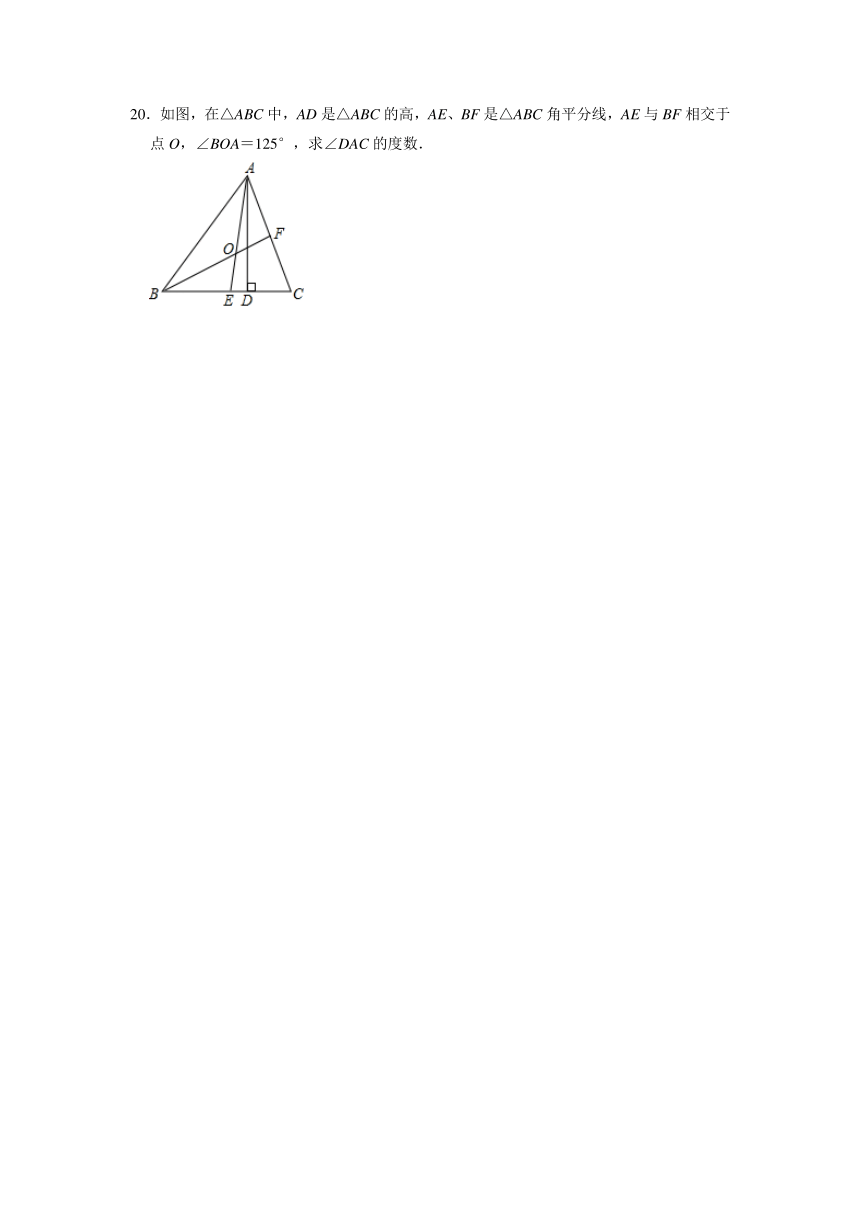
文档简介
2022-2023学年人教版(五四学制)七年级数学下册《第18章全等三角形》
期末综合复习题(附答案)
一、选择题(共计24分)
1.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
2.如图,在△ABD和△ACD中,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE:S△ACD=BD:AC,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
5.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
6.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
7.如图,△ABC≌△DEF,DF和AC,EF和BC为对应边,若∠A=123°,∠F=39°,则∠DEF等于( )
A.18° B.20° C.39° D.123°
8.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D.16
二、填空题(共计15分,)
9.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
10.如图,根据作图痕迹可知∠ADC= .
11.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
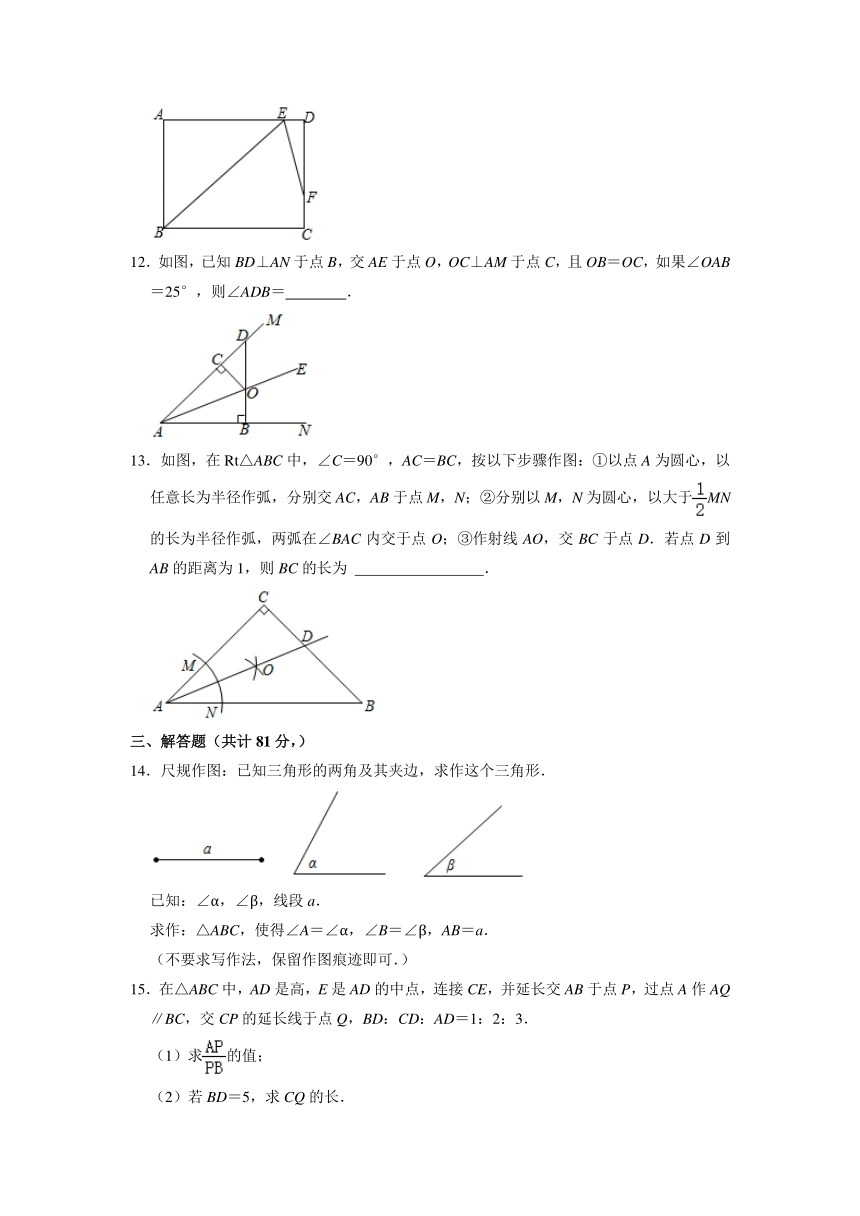
12.如图,已知BD⊥AN于点B,交AE于点O,OC⊥AM于点C,且OB=OC,如果∠OAB=25°,则∠ADB= .
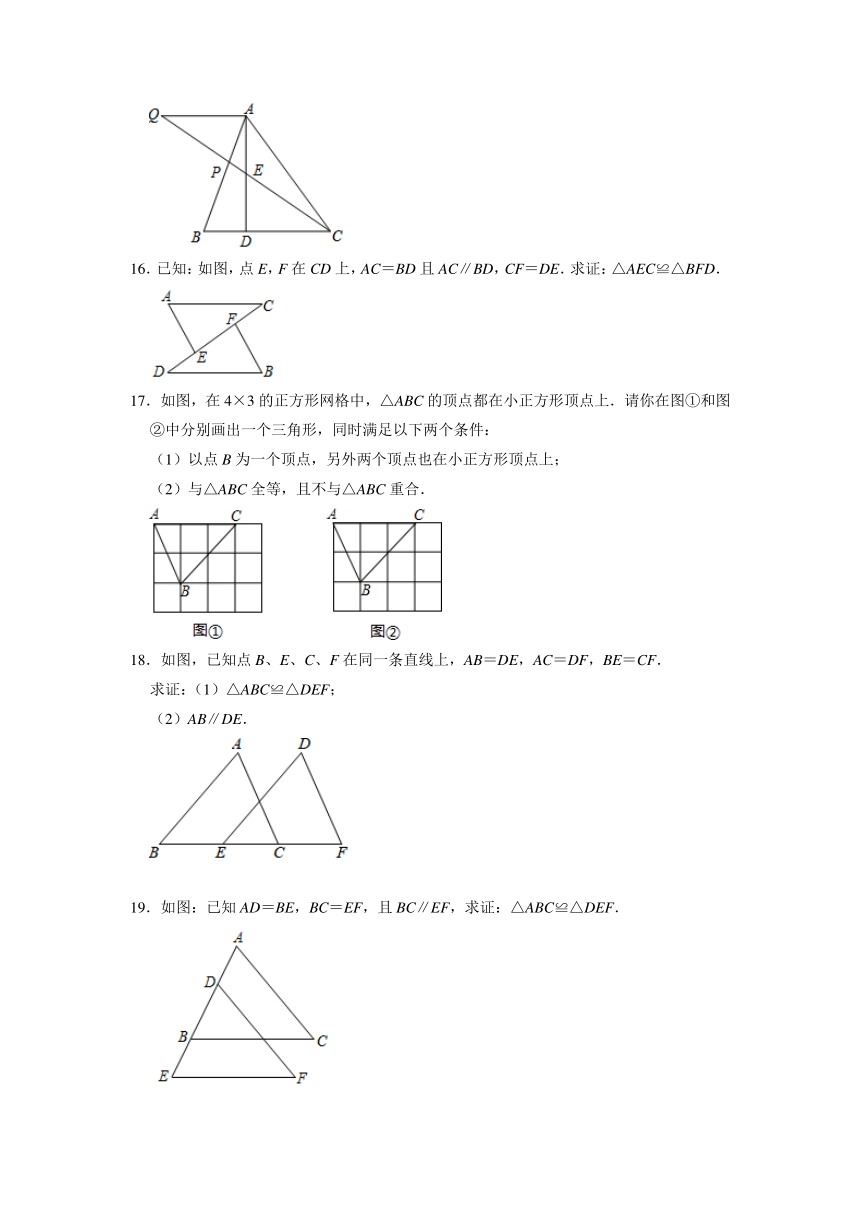
13.如图,在Rt△ABC中,∠C=90°,AC=BC,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC内交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则BC的长为 .
三、解答题(共计81分,)
14.尺规作图:已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段a.
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=a.
(不要求写作法,保留作图痕迹即可.)
15.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
16.已知:如图,点E,F在CD上,AC=BD且AC∥BD,CF=DE.求证:△AEC≌△BFD.
17.如图,在4×3的正方形网格中,△ABC的顶点都在小正方形顶点上.请你在图①和图②中分别画出一个三角形,同时满足以下两个条件:
(1)以点B为一个顶点,另外两个顶点也在小正方形顶点上;
(2)与△ABC全等,且不与△ABC重合.
18.如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC≌△DEF;
(2)AB∥DE.
19.如图:已知AD=BE,BC=EF,且BC∥EF,求证:△ABC≌△DEF.
20.如图,在△ABC中,AD是△ABC的高,AE、BF是△ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
参考答案
一、选择题(共计24分,)
1.解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
2.解:在△ABC中,∵∠B=∠C,
∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.
故选:A.
3.解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤错误,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故选:C.
4.解:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
故选:D.
5.解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
6.解:∵图中的两个三角形全等
a与a,c与c分别是对应边,那么它们的夹角就是对应角
∴∠α=50°
故选:D.
7.解;∵△ABC≌△DEF,∠A=123°,
∴∠D=∠A=123°,
∵∠F=39°,
∴∠DEF=180°﹣123°﹣39°=18°,
故选:A.
8.解:∵折叠
∴∠BFE=∠EFB'=60°,AB=A'B'∠A=∠A'=90°,AE=A'E=2
∵ABCD是矩形
∴AD∥BC
∴∠DEF=∠EFB=60°
∵A'E∥B'F
∴∠A'EF+∠EFB'=180°
∴∠A'EF=120°
∴∠A'EB'=60°且∠A'=90°
∴∠A'B'E=30°,且A'E=2
∴B'E=4,A'B'=2=AB
∵AE=2,DE=6
∴AD=8
∴S矩形ABCD=AB×AD=2×8=16
故选:D.
二、填空题(本题共计5小题,每题3分,共计15分,)
9.解:AC=DE,
理由是:∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL).
故答案为:AC=DE.
10.解:∵∠C=90°,∠B=50°,
∴∠CAB=90°﹣50°=40°,
由作图可知,AD平分∠CAB,
∴∠DAB=∠CAB=20°,
∴∠ADC=∠DAB+∠B=20°+50°=70°,
故答案为:70°.
11.解:延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE=,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴=9+2x+x
解得x=
∴BC=9+2(﹣3)=
故答案为:
12.解:∵DB⊥AN于B,OC⊥AM于点C,且OB=OC,
∴AE平分∠MAN,
∵∠OAB=25°,
∴∠MAN=50°,
∵DB⊥AN于B,
∴Rt△ABD中,∠ADB=40°,
故答案为:40°.
13.解:过点D作DH⊥AB,则DH=1,
由题目作图知,AD是∠CAB的平分线,
则CD=DH=1,
∵△ABC为等腰直角三角形,故∠B=45°,
则△DHB为等腰直角三角形,故BD=HD=,
则BC=CD+BD=1+,
故答案为:1+.
三、解答题(共计81分,)
14.解:如图,△ABC即为所求.
15.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
CE=,
∴CQ=25.
16.解:∵AC∥BD,
∴∠C=∠D,
∵CF=DE,
∴CF+EF=DE+EF,
即CE=DF,
在△AEC和△BFD中,
,
∴△AEC≌△BFD(SAS).
17.解:以下答案供参考:
画对一个得,画对两个得(6分).
18.证明:(1)∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
(2)∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE(同位角相等,两直线平行).
19.证明:∵BC∥EF,
∴∠CBA=∠E,
∵AD=BE,
∴AD+DB=BE+DB,
即:AB=DE,
在△ABC和△DEF,
,
∴△ABC≌△DEF(SAS).
20.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
期末综合复习题(附答案)
一、选择题(共计24分)
1.下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
2.如图,在△ABD和△ACD中,AB=AC,BD=CD,则△ABD≌△ACD的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中,与这100°角对应相等的角是( )
A.∠A B.∠B C.∠C D.∠B或∠C
4.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤S△BDE:S△ACD=BD:AC,其中正确的个数为( )
A.5个 B.4个 C.3个 D.2个
5.某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是( )
A.带①去 B.带②去 C.带③去 D.①②③都带去
6.已知图中的两个三角形全等,则∠α的度数是( )
A.72° B.60° C.58° D.50°
7.如图,△ABC≌△DEF,DF和AC,EF和BC为对应边,若∠A=123°,∠F=39°,则∠DEF等于( )
A.18° B.20° C.39° D.123°
8.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是( )
A.12 B.24 C.12 D.16
二、填空题(共计15分,)
9.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
10.如图,根据作图痕迹可知∠ADC= .
11.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
12.如图,已知BD⊥AN于点B,交AE于点O,OC⊥AM于点C,且OB=OC,如果∠OAB=25°,则∠ADB= .
13.如图,在Rt△ABC中,∠C=90°,AC=BC,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于MN的长为半径作弧,两弧在∠BAC内交于点O;③作射线AO,交BC于点D.若点D到AB的距离为1,则BC的长为 .
三、解答题(共计81分,)
14.尺规作图:已知三角形的两角及其夹边,求作这个三角形.
已知:∠α,∠β,线段a.
求作:△ABC,使得∠A=∠α,∠B=∠β,AB=a.
(不要求写作法,保留作图痕迹即可.)
15.在△ABC中,AD是高,E是AD的中点,连接CE,并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
(1)求的值;
(2)若BD=5,求CQ的长.
16.已知:如图,点E,F在CD上,AC=BD且AC∥BD,CF=DE.求证:△AEC≌△BFD.
17.如图,在4×3的正方形网格中,△ABC的顶点都在小正方形顶点上.请你在图①和图②中分别画出一个三角形,同时满足以下两个条件:
(1)以点B为一个顶点,另外两个顶点也在小正方形顶点上;
(2)与△ABC全等,且不与△ABC重合.
18.如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:(1)△ABC≌△DEF;
(2)AB∥DE.
19.如图:已知AD=BE,BC=EF,且BC∥EF,求证:△ABC≌△DEF.
20.如图,在△ABC中,AD是△ABC的高,AE、BF是△ABC角平分线,AE与BF相交于点O,∠BOA=125°,求∠DAC的度数.
参考答案
一、选择题(共计24分,)
1.解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
2.解:在△ABC中,∵∠B=∠C,
∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.
故选:A.
3.解:①正确,∵在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,
∴CD=ED;
②正确,因为由HL可知△ADC≌△ADE,所以AC=AE,即AC+BE=AB;
③正确,因为∠BDE和∠BAC都与∠B互余,根据同角的余角相等,所以∠BDE=∠BAC;
④错误,因为∠B的度数不确定,故BE不一定等于DE;
⑤错误,因为CD=ED,△ABD和△ACD的高相等,所以S△BDE:S△ACD=BE:AC.
故选:C.
4.解:在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
故选:D.
5.解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;
第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.
故选:C.
6.解:∵图中的两个三角形全等
a与a,c与c分别是对应边,那么它们的夹角就是对应角
∴∠α=50°
故选:D.
7.解;∵△ABC≌△DEF,∠A=123°,
∴∠D=∠A=123°,
∵∠F=39°,
∴∠DEF=180°﹣123°﹣39°=18°,
故选:A.
8.解:∵折叠
∴∠BFE=∠EFB'=60°,AB=A'B'∠A=∠A'=90°,AE=A'E=2
∵ABCD是矩形
∴AD∥BC
∴∠DEF=∠EFB=60°
∵A'E∥B'F
∴∠A'EF+∠EFB'=180°
∴∠A'EF=120°
∴∠A'EB'=60°且∠A'=90°
∴∠A'B'E=30°,且A'E=2
∴B'E=4,A'B'=2=AB
∵AE=2,DE=6
∴AD=8
∴S矩形ABCD=AB×AD=2×8=16
故选:D.
二、填空题(本题共计5小题,每题3分,共计15分,)
9.解:AC=DE,
理由是:∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL).
故答案为:AC=DE.
10.解:∵∠C=90°,∠B=50°,
∴∠CAB=90°﹣50°=40°,
由作图可知,AD平分∠CAB,
∴∠DAB=∠CAB=20°,
∴∠ADC=∠DAB+∠B=20°+50°=70°,
故答案为:70°.
11.解:延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,
∴∠ABE=∠AEB=45°,
∴AB=AE=9,
∴直角三角形ABE中,BE=,
又∵∠BED的角平分线EF与DC交于点F,
∴∠BEG=∠DEF
∵AD∥BC
∴∠G=∠DEF
∴∠BEG=∠G
∴BG=BE=
设CG=x,DE=2x,则AD=9+2x=BC
∵BG=BC+CG
∴=9+2x+x
解得x=
∴BC=9+2(﹣3)=
故答案为:
12.解:∵DB⊥AN于B,OC⊥AM于点C,且OB=OC,
∴AE平分∠MAN,
∵∠OAB=25°,
∴∠MAN=50°,
∵DB⊥AN于B,
∴Rt△ABD中,∠ADB=40°,
故答案为:40°.
13.解:过点D作DH⊥AB,则DH=1,
由题目作图知,AD是∠CAB的平分线,
则CD=DH=1,
∵△ABC为等腰直角三角形,故∠B=45°,
则△DHB为等腰直角三角形,故BD=HD=,
则BC=CD+BD=1+,
故答案为:1+.
三、解答题(共计81分,)
14.解:如图,△ABC即为所求.
15.解:(1)设BD=x,则CD=2x,AD=3x,BC=BD+CD=3x,
∵AQ∥BC,
∴==1,
∴AQ=CD=2x,
∴==;
(2)∵BD=5,BD:CD:AD=1:2:3,
∴CD=10,AD=15,
∵E是AD的中点,
∴DE=AD=7.5,
CE=,
∴CQ=25.
16.解:∵AC∥BD,
∴∠C=∠D,
∵CF=DE,
∴CF+EF=DE+EF,
即CE=DF,
在△AEC和△BFD中,
,
∴△AEC≌△BFD(SAS).
17.解:以下答案供参考:
画对一个得,画对两个得(6分).
18.证明:(1)∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
(2)∵△ABC≌△DEF,
∴∠B=∠DEF,
∴AB∥DE(同位角相等,两直线平行).
19.证明:∵BC∥EF,
∴∠CBA=∠E,
∵AD=BE,
∴AD+DB=BE+DB,
即:AB=DE,
在△ABC和△DEF,
,
∴△ABC≌△DEF(SAS).
20.解:∵∠OAB+∠OBA+∠AOB=180°,∠AOB=125°,
∴∠OAB+∠OBA=180°﹣125°=55°,
∵AE、BF是△ABC角平分线,
∴∠OAB=∠BAC,∠OBA=∠ABC,
∴∠BAC+∠ABC=55°,
∴∠BAC+∠ABC=110°,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠ACB=70°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠DAC=90°﹣70°=20°.
同课章节目录
