课堂分层优化系列之拓展培优练10.3 课题学习从数据谈节水三(含解析)
文档属性
| 名称 | 课堂分层优化系列之拓展培优练10.3 课题学习从数据谈节水三(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
课堂分层优化系列之拓展培优练10.3课题学习从数据谈节水(三)
一.选择题(共8小题,每小题4分,共32分)
1.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
2.一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多20人,则这次问卷调查的总人数为( )
A.120人 B.160人 C.200人 D.240人
3.某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( )
A.参加此次问卷调查的学生人数是45人
B.在条形统计图中,选择“作品2”的人数为15人
C.在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是65°
D.在扇形统计图中,选择“作品3”的学生所占百分比为36%
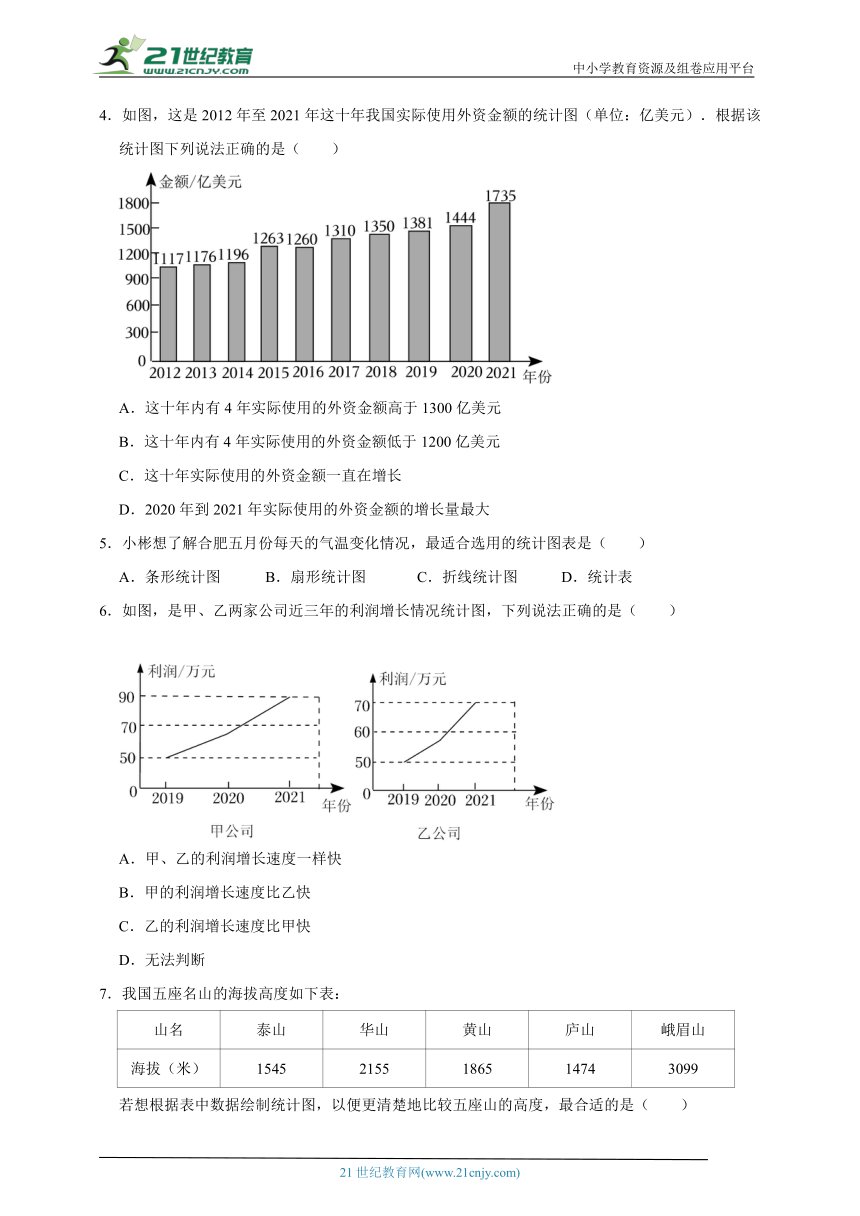
4.如图,这是2012年至2021年这十年我国实际使用外资金额的统计图(单位:亿美元).根据该统计图下列说法正确的是( )
A.这十年内有4年实际使用的外资金额高于1300亿美元
B.这十年内有4年实际使用的外资金额低于1200亿美元
C.这十年实际使用的外资金额一直在增长
D.2020年到2021年实际使用的外资金额的增长量最大
5.小彬想了解合肥五月份每天的气温变化情况,最适合选用的统计图表是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
6.如图,是甲、乙两家公司近三年的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快
B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快
D.无法判断
7.我国五座名山的海拔高度如下表:
山名 泰山 华山 黄山 庐山 峨眉山
海拔(米) 1545 2155 1865 1474 3099
若想根据表中数据绘制统计图,以便更清楚地比较五座山的高度,最合适的是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
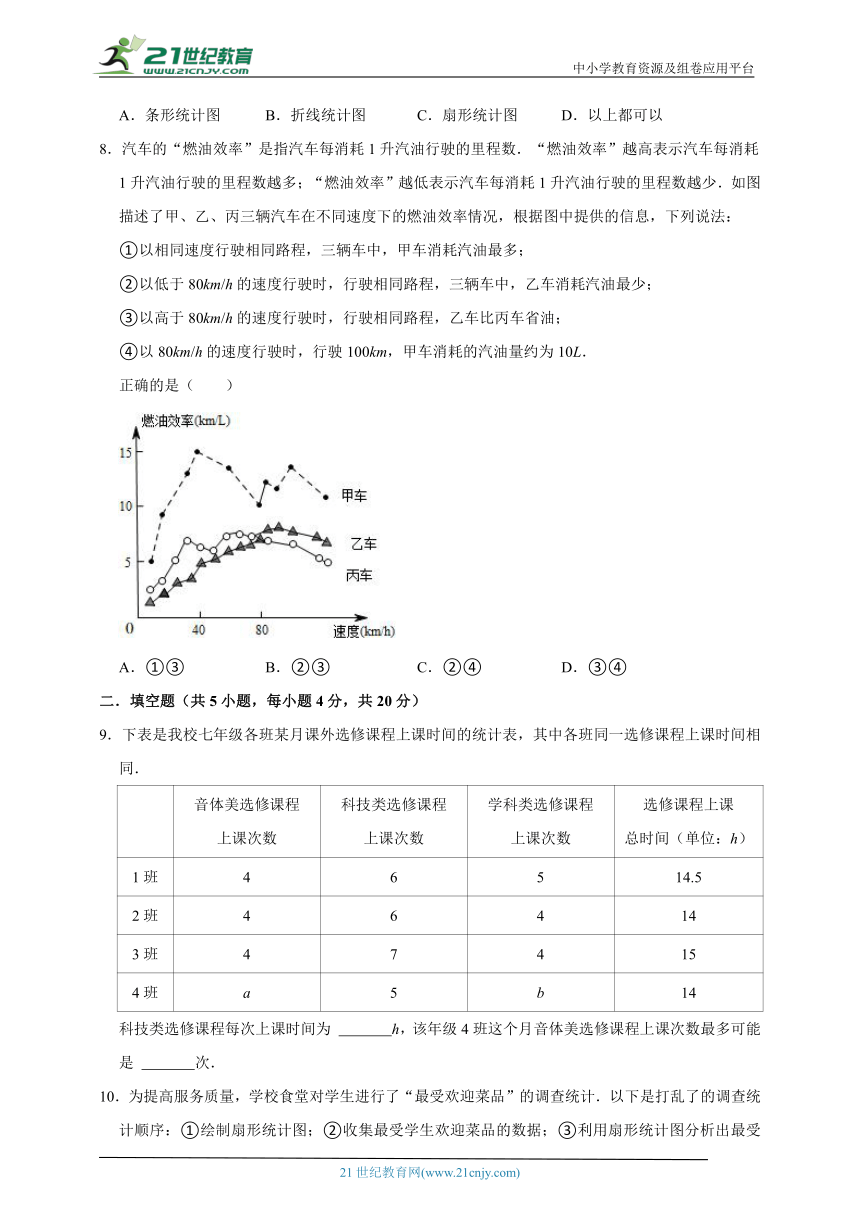
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,根据图中提供的信息,下列说法:
①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多;
②以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少;
③以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油;
④以80km/h的速度行驶时,行驶100km,甲车消耗的汽油量约为10L.
正确的是( )
A.①③ B.②③ C.②④ D.③④
二.填空题(共5小题,每小题4分,共20分)
9.下表是我校七年级各班某月课外选修课程上课时间的统计表,其中各班同一选修课程上课时间相同.
音体美选修课程上课次数 科技类选修课程上课次数 学科类选修课程上课次数 选修课程上课总时间(单位:h)
1班 4 6 5 14.5
2班 4 6 4 14
3班 4 7 4 15
4班 a 5 b 14
科技类选修课程每次上课时间为 h,该年级4班这个月音体美选修课程上课次数最多可能是 次.
10.为提高服务质量,学校食堂对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序:①绘制扇形统计图;②收集最受学生欢迎菜品的数据;③利用扇形统计图分析出最受学生欢迎的菜品;④整理所收集的数据.请按正确的调查统计顺序重新排序(只填序号): .
11.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取―部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:A.加大倡议宣传力度;B.加大罚款力度;C.明确倡议细则;D.增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中∠α的度数为 .
12.如图,下面的折线图反映的是我区某家庭每天购菜费用情况(统计时间为一周),则这个星期中此家庭购菜费用最大值与最小值的差为 元.
13.某车队有8位司机:A、B、C、D、E、F、G、H.12月份用车耗去的汽油费用如下表,根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是 .
司机 A B C D E F G H
耗油费用/元 110 105 99 125 100 95 145 108
三.解答题(共6小题,每小题8分,共48分)
14.“不忘初心,继续前行”,2017年10月18日﹣2017年10月24日“中国共产党第十九次全国代表大会”在北京隆重召开,为了解某校1000名学生在此期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“中国共产党第十九次全国代表大会”期间对会议的关注方式的统计表
关注方式 频数 百分比
电视 23 46%
网络
报纸 8%
其他 15
合计 100%
(1)本次问卷调查抽取的学生共有 人,其中通过报纸关注会议的学生有 人.
(2)从上表“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过网络关注会议的约有多少人?
15.阅读下列材料:
2012年上半年出台规定,将用空气质量指数替代原有的空气污染指数.
空气质量按照空气质量指数大小分为六级.相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重.对人体的健康危害也就越大.从一级优、二级良、三级轻度污染、四级中度污染,直至五级重度污染,六级严重污染将空气质量达到一级优、二级良的天气定义为达标天气.
北京市环保局2017年1月3日上午向媒体通报:
2016年北京空气质量状况,与2015年相比,2016年,北京各项污染物同比均有所改善.据报导,2016年北京空气质量持续改善,PM2.5年均浓度73微克/立方米,同比下降9.4%.但是这一数值依旧超出国家标准109%.2016年,北京空气质量达标天数198天,较2015年增加12天,其中PM2.5一级优的天数增加了16天.2016年北京有重污染(含严重污染天)39天.其中2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%.空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天.2015年本市空气质量达标天数较2014年增加14天,其中PM2.5一级优的天数增加了13天.2015年本市PM2.5重污染天(含严重污染天)数占全年总天数的12.6%.其中在11﹣12月中发生重污染22天,占11月和12月天数的36%,与2014年同期相比增加15天.2014年北京市PM2.5一级优的天数达到39天,较2013年减少了2天,但PM2.5导致的重污染天(含严重污染天)数明显减少了11天,从2013年的58天下降为47天.
根据以上材料解答下列问题:
(1)2014年本市空气质量达标天数为 天;PM2.5年平均浓度的国家标准限值是 微克/立方米.(结果保留整数)
(2)选择统计表或统计图,将2014﹣2016年PM2.5一级优天数的情况表示出来;预估2017年北京市PM2.5一级优天数约 天.
(3)小明从报道中发现“2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%,空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天”,他由此推断“2016年全年的PM2.5达标天数的年增长率将比2015年全年的PM2.5达标天数的年增长率出现大幅增长”,你同意他的结论吗?并说明你的理由.
(PM2.5达标天数的年增长率=×100%
16.为了传承中华优秀传统文化,某校组织了一次七年级的“汉字听写”大赛,七年级1班学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,同学们把成绩进行整理,得到下列表格:
成绩(分) 50 60 70 80 90 100
人数 2 6 9 18 13 2
(1)七年级1班有 名学生;
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
成绩(分) 50 60 70 80 90 100
人数 6 9 7 9 15 4
请你谈谈哪个班的比赛成绩好些,并说明理由.
17.总务处为合理配置学校的体育器材,委托体育教研组调查了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等五项体育活动的喜欢程度.体育教研组随机抽查了部分学生,对同学们最喜欢的体育项目(每人只选一项)进行问卷调查,并将统计数据绘制成如下两幅不完整的统计图.
解答下列问题:
(1)填空:m= %,这次问卷调查共抽取了 名学生进行调查.
(2)补全图2中的条形统计图.
(3)若全校共有1800名学生,则该校约有多少名学生喜爱打篮球?
18.某中学为了了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面抽查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.
(1)在这次调查活动中,一共调查了 名学生;
(2)通过计算,“排球”所在扇形的圆心角是多少度?
(3)请补全折线统计图;
(4)若该校有学生1300名,估计爱好篮球活动的约有多少名学生?
19.诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 成绩分组(单位:分) 频数
A 50≤x<60 40
B 60≤x<70 a
C 70≤x<80 90
D 80≤x<90 b
E 90≤x<100 100
合计 c
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
课堂分层优化系列之拓展培优练10.3课题学习从数据谈节水(三)
参考答案与试题解析
一.选择题(共8小题,每小题4分,共32分)
1.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
【分析】根据频数、频率、总数之间的关系进行计算即可.
【解答】解:60×(1﹣35%﹣15%﹣10%)=24(人),
故选:D.
【点评】本题考查频数分布表,解答本题的关键是掌握频数=频率×数据总数.
2.一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多20人,则这次问卷调查的总人数为( )
A.120人 B.160人 C.200人 D.240人
【分析】用最喜爱足球比最喜爱游泳的人数多的人数除以最喜爱足球比最喜爱游泳的人数多的百分比即可得出答案.
【解答】解:根据题意,可得20÷(30%﹣20%)=200(人),
即这次问卷调查的总人数为200人.
故选:C.
【点评】本题考查扇形统计图及相关计算.扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
3.某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( )
A.参加此次问卷调查的学生人数是45人
B.在条形统计图中,选择“作品2”的人数为15人
C.在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是65°
D.在扇形统计图中,选择“作品3”的学生所占百分比为36%
【分析】根据“作品4”的人数和所占的百分比,求出调查的学生总人数;用调查的学生总人数分别减去其它三个作品的人数可得“作品2”的人数;用选择“作品1”的学生数除以总人数,再乘以360°即可得出答案;用选择“作品3”的学生数除以总人数,可得选择“作品3”的学生所占百分比.
【解答】解:参加此次问卷调查的学生人数是:7÷14%=50(人),故选项A不符合题意;
在条形统计图中,选择“作品2”的人数为:50﹣9﹣18﹣7=16(人),故选项B不符合题意;
在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是360°×=64.8°,故选项C不符合题意;
在扇形统计图中,选择“作品3”的学生所占百分比为18÷50=36%,故选项D符合题意.
故选:D.
【点评】本题考查扇形统计图、条形统计图的意义和制作方法,从统计图中获取数量和数量之间的关系,是解决问题的前提.
4.如图,这是2012年至2021年这十年我国实际使用外资金额的统计图(单位:亿美元).根据该统计图下列说法正确的是( )
A.这十年内有4年实际使用的外资金额高于1300亿美元
B.这十年内有4年实际使用的外资金额低于1200亿美元
C.这十年实际使用的外资金额一直在增长
D.2020年到2021年实际使用的外资金额的增长量最大
【分析】分析统计图上的信息即可得出正确结论.
【解答】解:由统计图可知:
这十年内有5年实际使用的外资金额高于1300亿美元,故选项A不符合题意;
这十年内有3年实际使用的外资金额低于1200亿美元,故选项B不符合题意;
这十年实际使用的外资金额在2015至2016年下降,故选项C不符合题意;
2020年到2021年实际使用的外资金额的增长量最大,故选项D符合题意.
故选:D.
【点评】本题主要考查了条形统计图,解题的关键是读懂统计图,从统计图上获得正确的信息.
5.小彬想了解合肥五月份每天的气温变化情况,最适合选用的统计图表是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
【分析】根据扇形统计图、折线统计图、条形统计图各自的特点来判断即可.
【解答】解:根据统计图的特点,想了解合肥五月份每天的气温变化情况,最适合使用的统计图是折线统计图.
故选:C.
【点评】此题主要考查了统计图的选择.根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
6.如图,是甲、乙两家公司近三年的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快
B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快
D.无法判断
【分析】利用折线统计图求增长率,再进行比较.
【解答】解:甲的利润增长速度为:(90﹣50)÷50=0.8,
乙的利润增长速度为:(70﹣50)÷50=0.4,
0.8>0.4,
故选:B.
【点评】本题考查了折线统计图,求增长率是解题的关键.
7.我国五座名山的海拔高度如下表:
山名 泰山 华山 黄山 庐山 峨眉山
海拔(米) 1545 2155 1865 1474 3099
若想根据表中数据绘制统计图,以便更清楚地比较五座山的高度,最合适的是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,知:要求直观比较五座山的高度,结合统计图各自的特点,应选择条形统计图.
故选:A.
【点评】本题主要考查统计图的选择,根据扇形统计图、折线统计图、条形统计图各自的特点来判断.
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,根据图中提供的信息,下列说法:
①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多;
②以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少;
③以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油;
④以80km/h的速度行驶时,行驶100km,甲车消耗的汽油量约为10L.
正确的是( )
A.①③ B.②③ C.②④ D.③④
【分析】根据题意和函数图象可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解:由图可得,
以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故①错误,
以低于80km/h的速度行驶时,行驶相同路程,三辆车中,甲车消耗汽油最少,故②错误,
以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油,故③正确,
以80km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升,故④正确,
故选:D.
【点评】本题考查函数的图象,解答本题的关键是读懂图象信息,灵活运用所学知识解决问题.
二.填空题(共5小题,每小题4分,共20分)
9.下表是我校七年级各班某月课外选修课程上课时间的统计表,其中各班同一选修课程上课时间相同.
音体美选修课程上课次数 科技类选修课程上课次数 学科类选修课程上课次数 选修课程上课总时间(单位:h)
1班 4 6 5 14.5
2班 4 6 4 14
3班 4 7 4 15
4班 a 5 b 14
科技类选修课程每次上课时间为 1 h,该年级4班这个月音体美选修课程上课次数最多可能是 6 次.
【分析】设音体美选修课程上课时间每次为xh,科技类选修课程每次上课时间为yh,学科类选修课程每次上课时间为zh,构建方程组求出x,y,z,则1.5a+5+0.5b=14,求出整数解,可得结论.
【解答】解:设音体美选修课程上课时间每次为xh,科技类选修课程每次上课时间为yh,学科类选修课程每次上课时间为zh,
则有,解得,
∴1.5a+5+0.5b=14,
即3a+b=18,
∴当b=0时,a最大为6,
∴该年级4班这个月音体美选修课程上课次数最多可能是6次.
故答案为:1,6.
【点评】本题考查统计表,解题的关键是理解题意,学会利用参数构建方程组或方程解决问题,属于中考常考题型.
10.为提高服务质量,学校食堂对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序:①绘制扇形统计图;②收集最受学生欢迎菜品的数据;③利用扇形统计图分析出最受学生欢迎的菜品;④整理所收集的数据.请按正确的调查统计顺序重新排序(只填序号): ②④①③ .
【分析】根据收据的收集、整理及扇形统计图的制作步骤求解可得.
【解答】解:正确的调查统计顺序为:②收集最受学生欢迎菜品的数据;④整理所收集的数据;①绘制扇形统计图;③利用扇形统计图分析出最受学生欢迎的菜品;
故答案为:②④①③.
【点评】本题主要考查扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
11.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取―部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:A.加大倡议宣传力度;B.加大罚款力度;C.明确倡议细则;D.增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中∠α的度数为 36° .
【分析】利用A的本数已经百分比求出总数,再求出D的百分数,可得结论.
【解答】解:由题意总数==200(本),
∵D占=10%,
∴圆心角α=360°×10%=36°,
故答案为:36°.
【点评】本题考查条形统计图,条形统计图等知识,解题的关键是知道圆心角=360°×百分比.
12.如图,下面的折线图反映的是我区某家庭每天购菜费用情况(统计时间为一周),则这个星期中此家庭购菜费用最大值与最小值的差为 20 元.
【分析】根据题意和统计图中的数据可以求得这个星期中此家庭购菜费用最大值与最小值的差.
【解答】解:由题意可得,
这个星期中此家庭购菜费用最大值与最小值的差为:30﹣10=20(元),
故答案为:20.
【点评】本题考查折线统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
13.某车队有8位司机:A、B、C、D、E、F、G、H.12月份用车耗去的汽油费用如下表,根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是 条形统计图 .
司机 A B C D E F G H
耗油费用/元 110 105 99 125 100 95 145 108
【分析】根据条形统计图,扇形统计图,以及折线统计图的特点判断即可.
【解答】解:根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是条形统计图,
故答案为:条形统计图
【点评】此题考查了统计图的选择,统计表,弄清各种统计图的特征是解本题的关键.
三.解答题(共6小题,每小题8分,共48分)
14.“不忘初心,继续前行”,2017年10月18日﹣2017年10月24日“中国共产党第十九次全国代表大会”在北京隆重召开,为了解某校1000名学生在此期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“中国共产党第十九次全国代表大会”期间对会议的关注方式的统计表
关注方式 频数 百分比
电视 23 46%
网络
报纸 8%
其他 15
合计 100%
(1)本次问卷调查抽取的学生共有 50 人,其中通过报纸关注会议的学生有 4 人.
(2)从上表“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过网络关注会议的约有多少人?
【分析】(1)由问卷调查的学生总人数=通过电视关注的学生人数÷该项人数所占的百分比;通过报纸关注会议的学生人数=问卷调查的学生总人数×该项人数所占的百分比;
(2)可选择条形图或者扇形图;
(3)该校学生通过网络关注会议的人数=该校学生数×该项所占的百分数.
【解答】解:(1)23÷46%=50(人),
50×8%=4(人).
答:本次问卷调查抽取的学生共有50人,其中通过报纸关注会议的学生有4人.
故答案为:50,4;
(2)通过网络关注会议的学生有50﹣23﹣4﹣15=8(人).
选择条形图,如图所示:
(3)1 000×=160(人).
答:估计该校学生通过网络关注会议的约有160人.
【点评】本题考查了频数、频率及总数间的关系,统计图的选择和用样本估计总数.频率=,频数=频率×数据总数,总数=.
15.阅读下列材料:
2012年上半年出台规定,将用空气质量指数替代原有的空气污染指数.
空气质量按照空气质量指数大小分为六级.相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重.对人体的健康危害也就越大.从一级优、二级良、三级轻度污染、四级中度污染,直至五级重度污染,六级严重污染将空气质量达到一级优、二级良的天气定义为达标天气.
北京市环保局2017年1月3日上午向媒体通报:
2016年北京空气质量状况,与2015年相比,2016年,北京各项污染物同比均有所改善.据报导,2016年北京空气质量持续改善,PM2.5年均浓度73微克/立方米,同比下降9.4%.但是这一数值依旧超出国家标准109%.2016年,北京空气质量达标天数198天,较2015年增加12天,其中PM2.5一级优的天数增加了16天.2016年北京有重污染(含严重污染天)39天.其中2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%.空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天.2015年本市空气质量达标天数较2014年增加14天,其中PM2.5一级优的天数增加了13天.2015年本市PM2.5重污染天(含严重污染天)数占全年总天数的12.6%.其中在11﹣12月中发生重污染22天,占11月和12月天数的36%,与2014年同期相比增加15天.2014年北京市PM2.5一级优的天数达到39天,较2013年减少了2天,但PM2.5导致的重污染天(含严重污染天)数明显减少了11天,从2013年的58天下降为47天.
根据以上材料解答下列问题:
(1)2014年本市空气质量达标天数为 172 天;PM2.5年平均浓度的国家标准限值是 35 微克/立方米.(结果保留整数)
(2)选择统计表或统计图,将2014﹣2016年PM2.5一级优天数的情况表示出来;预估2017年北京市PM2.5一级优天数约 8 4 天.
(3)小明从报道中发现“2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%,空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天”,他由此推断“2016年全年的PM2.5达标天数的年增长率将比2015年全年的PM2.5达标天数的年增长率出现大幅增长”,你同意他的结论吗?并说明你的理由.
(PM2.5达标天数的年增长率=×100%
【分析】(1)根据:“2015年本市空气质量达标天数为186天,较2014年增加14天“可知2014年本市空气质量达标天数,根据:“2015年北京缓解空气中PM2.5年均浓度为80.6微克/立方米,约为国家标准限值的2.3倍“可知PM2.5年平均浓度的国家标准限值;
(2)列统计表即可;
(3)通过计算知2016年和2015年增长率,故不同意.
【解答】解:(1)2014年本市空气质量达标天数为186﹣14=172(天);
PM2.5年平均浓度的国家标准限值是80.6÷2.3≈35(微克/立方米);
(2)填表如下:
年份 PM2.5一级优天数
2014年 39天
2015年 52天
2016年 68天
预2017年一级优天84天.
(3)不同意.2016年增长率:×100%=65%,2015年增长率:×100%=8%,6%<8%,
故没有增长.
故答案为:(1)172,35.(2)84.
【点评】本题主要考查统计图的选择与制作,阅读资料理清所涉数据是解题的关键.
16.为了传承中华优秀传统文化,某校组织了一次七年级的“汉字听写”大赛,七年级1班学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,同学们把成绩进行整理,得到下列表格:
成绩(分) 50 60 70 80 90 100
人数 2 6 9 18 13 2
(1)七年级1班有 50 名学生;
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
成绩(分) 50 60 70 80 90 100
人数 6 9 7 9 15 4
请你谈谈哪个班的比赛成绩好些,并说明理由.
【分析】(1)根据表格中数据即可得出答案;
(2)选择条形图、折线图,即可解答;
(3)根据中位数和众数以及平均数,即可解答.
【解答】解:(1)2+6+9+18+13+2=50;
故答案为:50;
(2)(任选其一);
(3)七年级1班成绩这组数据的中位数是80,众数是80,80分以上的有33人,
平均分为=78(分);
七年级2班成绩这组数据的中位数是80,众数是90;80分以上的有28人,
平均分为=76(分)
所以七年级1班的成绩较好.
【点评】本题考查了统计图的选择,解决本题的关键是熟记统计图的特点.
17.总务处为合理配置学校的体育器材,委托体育教研组调查了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等五项体育活动的喜欢程度.体育教研组随机抽查了部分学生,对同学们最喜欢的体育项目(每人只选一项)进行问卷调查,并将统计数据绘制成如下两幅不完整的统计图.
解答下列问题:
(1)填空:m= 20 %,这次问卷调查共抽取了 50 名学生进行调查.
(2)补全图2中的条形统计图.
(3)若全校共有1800名学生,则该校约有多少名学生喜爱打篮球?
【分析】(1)由扇形统计图的知识,可求得m的值,继而求得抽取了的学生数,
(2)总数减去其它即可得乒乓球人数,可补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案;
【解答】解:(1)∵m%=1﹣14%﹣8%﹣24%﹣34%=20%,
∴m=20,
∵喜欢跳绳的占8%,有4人,
∴4÷8%=50(名),
∴共抽取了50名学生;
故答案为:20,50;
(2))喜欢乒乓球的:50×20%=10(名),
条形统计图如图所示;
(3)∵1800×24%=432,
∴该校约有432名学生喜爱打篮球.
【点评】本题考查了条形统计图,观察条形统计图、扇形统计图获得有效信息是解题关键.
18.某中学为了了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面抽查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.
(1)在这次调查活动中,一共调查了 300 名学生;
(2)通过计算,“排球”所在扇形的圆心角是多少度?
(3)请补全折线统计图;
(4)若该校有学生1300名,估计爱好篮球活动的约有多少名学生?
【分析】(1)根据羽毛球的人数和所占的百分比即可求出调查的学生数;
(2)根据圆心角=百分比×360°,计算即可;
(3)求出乒乓球、排球的人数即可解决问题;
(4)用样本估计总体的思想解决问题即可;
【解答】解:(1)本次调查学生人数为:90÷30%=300(名);
故答案为:300;
(2)由图可知,篮球人数为60,
乒乓球人数是300×40%=120,
则排球人数为300﹣60﹣90﹣120=30;
则排球所在的扇形圆心角是×360°=36°;
(3)折线统计图如图所示,
(4)1300×=260(名)
答:若该校有学生1300名,估计爱好篮球活动的约有260名学生.
【点评】本题考查学生的读图能力以及频率、频数的计算.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
19.诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 成绩分组(单位:分) 频数
A 50≤x<60 40
B 60≤x<70 a
C 70≤x<80 90
D 80≤x<90 b
E 90≤x<100 100
合计 c
根据以上信息解答下列问题:
(1)统计表中a= 70 ,b= 200 ,c= 500 ;
(2)扇形统计图中,m的值为 14 ,“E”所对应的圆心角的度数是 72 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
【分析】(1)根据统计图中的数据可以分别求得a、b、c的值;
(2)根据统计图中的数据可以求得m和“E”所对应的圆心角的度数;
(3)根据题意可以求得成绩在80分及以上的学生大约有多少人.
【解答】解:(1)a=(40÷8%)×(1﹣8%﹣18%﹣40%﹣20%)=70,
b=(40÷8%)×40%=200,
c=40÷8%=500,
故答案为:70,200,500;
(2)m%=1﹣8%﹣18%﹣40%﹣20%=14%,
“E”所对应的圆心角的度数是:360°×20%=72°,
故答案为:14,72;
(3)4000×(40%+20%)=2400(人),
答:成绩在80分及以上的学生大约有2400人.
【点评】本题考查扇形统计图、用样本估计总体、频数分布表,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
课堂分层优化系列之拓展培优练10.3课题学习从数据谈节水(三)
一.选择题(共8小题,每小题4分,共32分)
1.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
2.一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多20人,则这次问卷调查的总人数为( )
A.120人 B.160人 C.200人 D.240人
3.某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( )
A.参加此次问卷调查的学生人数是45人
B.在条形统计图中,选择“作品2”的人数为15人
C.在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是65°
D.在扇形统计图中,选择“作品3”的学生所占百分比为36%
4.如图,这是2012年至2021年这十年我国实际使用外资金额的统计图(单位:亿美元).根据该统计图下列说法正确的是( )
A.这十年内有4年实际使用的外资金额高于1300亿美元
B.这十年内有4年实际使用的外资金额低于1200亿美元
C.这十年实际使用的外资金额一直在增长
D.2020年到2021年实际使用的外资金额的增长量最大
5.小彬想了解合肥五月份每天的气温变化情况,最适合选用的统计图表是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
6.如图,是甲、乙两家公司近三年的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快
B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快
D.无法判断
7.我国五座名山的海拔高度如下表:
山名 泰山 华山 黄山 庐山 峨眉山
海拔(米) 1545 2155 1865 1474 3099
若想根据表中数据绘制统计图,以便更清楚地比较五座山的高度,最合适的是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,根据图中提供的信息,下列说法:
①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多;
②以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少;
③以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油;
④以80km/h的速度行驶时,行驶100km,甲车消耗的汽油量约为10L.
正确的是( )
A.①③ B.②③ C.②④ D.③④
二.填空题(共5小题,每小题4分,共20分)
9.下表是我校七年级各班某月课外选修课程上课时间的统计表,其中各班同一选修课程上课时间相同.
音体美选修课程上课次数 科技类选修课程上课次数 学科类选修课程上课次数 选修课程上课总时间(单位:h)
1班 4 6 5 14.5
2班 4 6 4 14
3班 4 7 4 15
4班 a 5 b 14
科技类选修课程每次上课时间为 h,该年级4班这个月音体美选修课程上课次数最多可能是 次.
10.为提高服务质量,学校食堂对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序:①绘制扇形统计图;②收集最受学生欢迎菜品的数据;③利用扇形统计图分析出最受学生欢迎的菜品;④整理所收集的数据.请按正确的调查统计顺序重新排序(只填序号): .
11.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取―部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:A.加大倡议宣传力度;B.加大罚款力度;C.明确倡议细则;D.增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中∠α的度数为 .
12.如图,下面的折线图反映的是我区某家庭每天购菜费用情况(统计时间为一周),则这个星期中此家庭购菜费用最大值与最小值的差为 元.
13.某车队有8位司机:A、B、C、D、E、F、G、H.12月份用车耗去的汽油费用如下表,根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是 .
司机 A B C D E F G H
耗油费用/元 110 105 99 125 100 95 145 108
三.解答题(共6小题,每小题8分,共48分)
14.“不忘初心,继续前行”,2017年10月18日﹣2017年10月24日“中国共产党第十九次全国代表大会”在北京隆重召开,为了解某校1000名学生在此期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“中国共产党第十九次全国代表大会”期间对会议的关注方式的统计表
关注方式 频数 百分比
电视 23 46%
网络
报纸 8%
其他 15
合计 100%
(1)本次问卷调查抽取的学生共有 人,其中通过报纸关注会议的学生有 人.
(2)从上表“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过网络关注会议的约有多少人?
15.阅读下列材料:
2012年上半年出台规定,将用空气质量指数替代原有的空气污染指数.
空气质量按照空气质量指数大小分为六级.相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重.对人体的健康危害也就越大.从一级优、二级良、三级轻度污染、四级中度污染,直至五级重度污染,六级严重污染将空气质量达到一级优、二级良的天气定义为达标天气.
北京市环保局2017年1月3日上午向媒体通报:
2016年北京空气质量状况,与2015年相比,2016年,北京各项污染物同比均有所改善.据报导,2016年北京空气质量持续改善,PM2.5年均浓度73微克/立方米,同比下降9.4%.但是这一数值依旧超出国家标准109%.2016年,北京空气质量达标天数198天,较2015年增加12天,其中PM2.5一级优的天数增加了16天.2016年北京有重污染(含严重污染天)39天.其中2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%.空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天.2015年本市空气质量达标天数较2014年增加14天,其中PM2.5一级优的天数增加了13天.2015年本市PM2.5重污染天(含严重污染天)数占全年总天数的12.6%.其中在11﹣12月中发生重污染22天,占11月和12月天数的36%,与2014年同期相比增加15天.2014年北京市PM2.5一级优的天数达到39天,较2013年减少了2天,但PM2.5导致的重污染天(含严重污染天)数明显减少了11天,从2013年的58天下降为47天.
根据以上材料解答下列问题:
(1)2014年本市空气质量达标天数为 天;PM2.5年平均浓度的国家标准限值是 微克/立方米.(结果保留整数)
(2)选择统计表或统计图,将2014﹣2016年PM2.5一级优天数的情况表示出来;预估2017年北京市PM2.5一级优天数约 天.
(3)小明从报道中发现“2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%,空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天”,他由此推断“2016年全年的PM2.5达标天数的年增长率将比2015年全年的PM2.5达标天数的年增长率出现大幅增长”,你同意他的结论吗?并说明你的理由.
(PM2.5达标天数的年增长率=×100%
16.为了传承中华优秀传统文化,某校组织了一次七年级的“汉字听写”大赛,七年级1班学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,同学们把成绩进行整理,得到下列表格:
成绩(分) 50 60 70 80 90 100
人数 2 6 9 18 13 2
(1)七年级1班有 名学生;
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
成绩(分) 50 60 70 80 90 100
人数 6 9 7 9 15 4
请你谈谈哪个班的比赛成绩好些,并说明理由.
17.总务处为合理配置学校的体育器材,委托体育教研组调查了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等五项体育活动的喜欢程度.体育教研组随机抽查了部分学生,对同学们最喜欢的体育项目(每人只选一项)进行问卷调查,并将统计数据绘制成如下两幅不完整的统计图.
解答下列问题:
(1)填空:m= %,这次问卷调查共抽取了 名学生进行调查.
(2)补全图2中的条形统计图.
(3)若全校共有1800名学生,则该校约有多少名学生喜爱打篮球?
18.某中学为了了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面抽查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.
(1)在这次调查活动中,一共调查了 名学生;
(2)通过计算,“排球”所在扇形的圆心角是多少度?
(3)请补全折线统计图;
(4)若该校有学生1300名,估计爱好篮球活动的约有多少名学生?
19.诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 成绩分组(单位:分) 频数
A 50≤x<60 40
B 60≤x<70 a
C 70≤x<80 90
D 80≤x<90 b
E 90≤x<100 100
合计 c
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
课堂分层优化系列之拓展培优练10.3课题学习从数据谈节水(三)
参考答案与试题解析
一.选择题(共8小题,每小题4分,共32分)
1.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
【分析】根据频数、频率、总数之间的关系进行计算即可.
【解答】解:60×(1﹣35%﹣15%﹣10%)=24(人),
故选:D.
【点评】本题考查频数分布表,解答本题的关键是掌握频数=频率×数据总数.
2.一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图.若最喜爱足球的人数比最喜爱游泳的人数多20人,则这次问卷调查的总人数为( )
A.120人 B.160人 C.200人 D.240人
【分析】用最喜爱足球比最喜爱游泳的人数多的人数除以最喜爱足球比最喜爱游泳的人数多的百分比即可得出答案.
【解答】解:根据题意,可得20÷(30%﹣20%)=200(人),
即这次问卷调查的总人数为200人.
故选:C.
【点评】本题考查扇形统计图及相关计算.扇形统计图是用整个圆表示总数,用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
3.某校举办了校服设计大赛,并从七年级学生中随机抽取部分学生进行问卷调查,要求每名学生从4个获奖作品中选择一个自己最喜欢的作品,根据调查结果绘制成如图所示的两幅不完整的统计图.请你根据图中信息判断下列说法正确的是( )
A.参加此次问卷调查的学生人数是45人
B.在条形统计图中,选择“作品2”的人数为15人
C.在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是65°
D.在扇形统计图中,选择“作品3”的学生所占百分比为36%
【分析】根据“作品4”的人数和所占的百分比,求出调查的学生总人数;用调查的学生总人数分别减去其它三个作品的人数可得“作品2”的人数;用选择“作品1”的学生数除以总人数,再乘以360°即可得出答案;用选择“作品3”的学生数除以总人数,可得选择“作品3”的学生所占百分比.
【解答】解:参加此次问卷调查的学生人数是:7÷14%=50(人),故选项A不符合题意;
在条形统计图中,选择“作品2”的人数为:50﹣9﹣18﹣7=16(人),故选项B不符合题意;
在扇形统计图中,选择“作品1”的学生所对应扇形的圆心角的度数是360°×=64.8°,故选项C不符合题意;
在扇形统计图中,选择“作品3”的学生所占百分比为18÷50=36%,故选项D符合题意.
故选:D.
【点评】本题考查扇形统计图、条形统计图的意义和制作方法,从统计图中获取数量和数量之间的关系,是解决问题的前提.
4.如图,这是2012年至2021年这十年我国实际使用外资金额的统计图(单位:亿美元).根据该统计图下列说法正确的是( )
A.这十年内有4年实际使用的外资金额高于1300亿美元
B.这十年内有4年实际使用的外资金额低于1200亿美元
C.这十年实际使用的外资金额一直在增长
D.2020年到2021年实际使用的外资金额的增长量最大
【分析】分析统计图上的信息即可得出正确结论.
【解答】解:由统计图可知:
这十年内有5年实际使用的外资金额高于1300亿美元,故选项A不符合题意;
这十年内有3年实际使用的外资金额低于1200亿美元,故选项B不符合题意;
这十年实际使用的外资金额在2015至2016年下降,故选项C不符合题意;
2020年到2021年实际使用的外资金额的增长量最大,故选项D符合题意.
故选:D.
【点评】本题主要考查了条形统计图,解题的关键是读懂统计图,从统计图上获得正确的信息.
5.小彬想了解合肥五月份每天的气温变化情况,最适合选用的统计图表是( )
A.条形统计图 B.扇形统计图 C.折线统计图 D.统计表
【分析】根据扇形统计图、折线统计图、条形统计图各自的特点来判断即可.
【解答】解:根据统计图的特点,想了解合肥五月份每天的气温变化情况,最适合使用的统计图是折线统计图.
故选:C.
【点评】此题主要考查了统计图的选择.根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
6.如图,是甲、乙两家公司近三年的利润增长情况统计图,下列说法正确的是( )
A.甲、乙的利润增长速度一样快
B.甲的利润增长速度比乙快
C.乙的利润增长速度比甲快
D.无法判断
【分析】利用折线统计图求增长率,再进行比较.
【解答】解:甲的利润增长速度为:(90﹣50)÷50=0.8,
乙的利润增长速度为:(70﹣50)÷50=0.4,
0.8>0.4,
故选:B.
【点评】本题考查了折线统计图,求增长率是解题的关键.
7.我国五座名山的海拔高度如下表:
山名 泰山 华山 黄山 庐山 峨眉山
海拔(米) 1545 2155 1865 1474 3099
若想根据表中数据绘制统计图,以便更清楚地比较五座山的高度,最合适的是( )
A.条形统计图 B.折线统计图 C.扇形统计图 D.以上都可以
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,知:要求直观比较五座山的高度,结合统计图各自的特点,应选择条形统计图.
故选:A.
【点评】本题主要考查统计图的选择,根据扇形统计图、折线统计图、条形统计图各自的特点来判断.
8.汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,根据图中提供的信息,下列说法:
①以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多;
②以低于80km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少;
③以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油;
④以80km/h的速度行驶时,行驶100km,甲车消耗的汽油量约为10L.
正确的是( )
A.①③ B.②③ C.②④ D.③④
【分析】根据题意和函数图象可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解:由图可得,
以相同速度行驶相同路程,三辆车中,甲车消耗汽油最少,故①错误,
以低于80km/h的速度行驶时,行驶相同路程,三辆车中,甲车消耗汽油最少,故②错误,
以高于80km/h的速度行驶时,行驶相同路程,乙车比丙车省油,故③正确,
以80km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升,故④正确,
故选:D.
【点评】本题考查函数的图象,解答本题的关键是读懂图象信息,灵活运用所学知识解决问题.
二.填空题(共5小题,每小题4分,共20分)
9.下表是我校七年级各班某月课外选修课程上课时间的统计表,其中各班同一选修课程上课时间相同.
音体美选修课程上课次数 科技类选修课程上课次数 学科类选修课程上课次数 选修课程上课总时间(单位:h)
1班 4 6 5 14.5
2班 4 6 4 14
3班 4 7 4 15
4班 a 5 b 14
科技类选修课程每次上课时间为 1 h,该年级4班这个月音体美选修课程上课次数最多可能是 6 次.
【分析】设音体美选修课程上课时间每次为xh,科技类选修课程每次上课时间为yh,学科类选修课程每次上课时间为zh,构建方程组求出x,y,z,则1.5a+5+0.5b=14,求出整数解,可得结论.
【解答】解:设音体美选修课程上课时间每次为xh,科技类选修课程每次上课时间为yh,学科类选修课程每次上课时间为zh,
则有,解得,
∴1.5a+5+0.5b=14,
即3a+b=18,
∴当b=0时,a最大为6,
∴该年级4班这个月音体美选修课程上课次数最多可能是6次.
故答案为:1,6.
【点评】本题考查统计表,解题的关键是理解题意,学会利用参数构建方程组或方程解决问题,属于中考常考题型.
10.为提高服务质量,学校食堂对学生进行了“最受欢迎菜品”的调查统计.以下是打乱了的调查统计顺序:①绘制扇形统计图;②收集最受学生欢迎菜品的数据;③利用扇形统计图分析出最受学生欢迎的菜品;④整理所收集的数据.请按正确的调查统计顺序重新排序(只填序号): ②④①③ .
【分析】根据收据的收集、整理及扇形统计图的制作步骤求解可得.
【解答】解:正确的调查统计顺序为:②收集最受学生欢迎菜品的数据;④整理所收集的数据;①绘制扇形统计图;③利用扇形统计图分析出最受学生欢迎的菜品;
故答案为:②④①③.
【点评】本题主要考查扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.
11.为促进城市交通更加文明,公共秩序更加优良,各个城市陆续发布“车让人”的倡议,此倡议得到了市民的一致赞赏.为了更好地完善“车让人”倡议,某市随机抽取―部分市民对“车让人”的倡议改进意见支持情况进行统计,分为四类:A.加大倡议宣传力度;B.加大罚款力度;C.明确倡议细则;D.增加监控路段,并将统计结果绘制成如图所示的两幅不完整的统计图.则扇形统计图中∠α的度数为 36° .
【分析】利用A的本数已经百分比求出总数,再求出D的百分数,可得结论.
【解答】解:由题意总数==200(本),
∵D占=10%,
∴圆心角α=360°×10%=36°,
故答案为:36°.
【点评】本题考查条形统计图,条形统计图等知识,解题的关键是知道圆心角=360°×百分比.
12.如图,下面的折线图反映的是我区某家庭每天购菜费用情况(统计时间为一周),则这个星期中此家庭购菜费用最大值与最小值的差为 20 元.
【分析】根据题意和统计图中的数据可以求得这个星期中此家庭购菜费用最大值与最小值的差.
【解答】解:由题意可得,
这个星期中此家庭购菜费用最大值与最小值的差为:30﹣10=20(元),
故答案为:20.
【点评】本题考查折线统计图,解答本题的关键是明确题意,利用数形结合的思想解答.
13.某车队有8位司机:A、B、C、D、E、F、G、H.12月份用车耗去的汽油费用如下表,根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是 条形统计图 .
司机 A B C D E F G H
耗油费用/元 110 105 99 125 100 95 145 108
【分析】根据条形统计图,扇形统计图,以及折线统计图的特点判断即可.
【解答】解:根据表中的数据作出统计图,以便更清楚地对每个人的耗油费用进行比较,那么应用最恰当的统计图是条形统计图,
故答案为:条形统计图
【点评】此题考查了统计图的选择,统计表,弄清各种统计图的特征是解本题的关键.
三.解答题(共6小题,每小题8分,共48分)
14.“不忘初心,继续前行”,2017年10月18日﹣2017年10月24日“中国共产党第十九次全国代表大会”在北京隆重召开,为了解某校1000名学生在此期间对会议的关注方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“中国共产党第十九次全国代表大会”期间对会议的关注方式的统计表
关注方式 频数 百分比
电视 23 46%
网络
报纸 8%
其他 15
合计 100%
(1)本次问卷调查抽取的学生共有 50 人,其中通过报纸关注会议的学生有 4 人.
(2)从上表“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)根据抽样的结果,估计该校学生通过网络关注会议的约有多少人?
【分析】(1)由问卷调查的学生总人数=通过电视关注的学生人数÷该项人数所占的百分比;通过报纸关注会议的学生人数=问卷调查的学生总人数×该项人数所占的百分比;
(2)可选择条形图或者扇形图;
(3)该校学生通过网络关注会议的人数=该校学生数×该项所占的百分数.
【解答】解:(1)23÷46%=50(人),
50×8%=4(人).
答:本次问卷调查抽取的学生共有50人,其中通过报纸关注会议的学生有4人.
故答案为:50,4;
(2)通过网络关注会议的学生有50﹣23﹣4﹣15=8(人).
选择条形图,如图所示:
(3)1 000×=160(人).
答:估计该校学生通过网络关注会议的约有160人.
【点评】本题考查了频数、频率及总数间的关系,统计图的选择和用样本估计总数.频率=,频数=频率×数据总数,总数=.
15.阅读下列材料:
2012年上半年出台规定,将用空气质量指数替代原有的空气污染指数.
空气质量按照空气质量指数大小分为六级.相对应空气质量的六个类别,指数越大、级别越高,说明污染的情况越严重.对人体的健康危害也就越大.从一级优、二级良、三级轻度污染、四级中度污染,直至五级重度污染,六级严重污染将空气质量达到一级优、二级良的天气定义为达标天气.
北京市环保局2017年1月3日上午向媒体通报:
2016年北京空气质量状况,与2015年相比,2016年,北京各项污染物同比均有所改善.据报导,2016年北京空气质量持续改善,PM2.5年均浓度73微克/立方米,同比下降9.4%.但是这一数值依旧超出国家标准109%.2016年,北京空气质量达标天数198天,较2015年增加12天,其中PM2.5一级优的天数增加了16天.2016年北京有重污染(含严重污染天)39天.其中2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%.空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天.2015年本市空气质量达标天数较2014年增加14天,其中PM2.5一级优的天数增加了13天.2015年本市PM2.5重污染天(含严重污染天)数占全年总天数的12.6%.其中在11﹣12月中发生重污染22天,占11月和12月天数的36%,与2014年同期相比增加15天.2014年北京市PM2.5一级优的天数达到39天,较2013年减少了2天,但PM2.5导致的重污染天(含严重污染天)数明显减少了11天,从2013年的58天下降为47天.
根据以上材料解答下列问题:
(1)2014年本市空气质量达标天数为 172 天;PM2.5年平均浓度的国家标准限值是 35 微克/立方米.(结果保留整数)
(2)选择统计表或统计图,将2014﹣2016年PM2.5一级优天数的情况表示出来;预估2017年北京市PM2.5一级优天数约 8 4 天.
(3)小明从报道中发现“2016年1月至8月底,北京全市PM2.5浓度同比下降12.5%,空气质量达标天数较去年同期增加19天,空气重污染天数同比减少5天”,他由此推断“2016年全年的PM2.5达标天数的年增长率将比2015年全年的PM2.5达标天数的年增长率出现大幅增长”,你同意他的结论吗?并说明你的理由.
(PM2.5达标天数的年增长率=×100%
【分析】(1)根据:“2015年本市空气质量达标天数为186天,较2014年增加14天“可知2014年本市空气质量达标天数,根据:“2015年北京缓解空气中PM2.5年均浓度为80.6微克/立方米,约为国家标准限值的2.3倍“可知PM2.5年平均浓度的国家标准限值;
(2)列统计表即可;
(3)通过计算知2016年和2015年增长率,故不同意.
【解答】解:(1)2014年本市空气质量达标天数为186﹣14=172(天);
PM2.5年平均浓度的国家标准限值是80.6÷2.3≈35(微克/立方米);
(2)填表如下:
年份 PM2.5一级优天数
2014年 39天
2015年 52天
2016年 68天
预2017年一级优天84天.
(3)不同意.2016年增长率:×100%=65%,2015年增长率:×100%=8%,6%<8%,
故没有增长.
故答案为:(1)172,35.(2)84.
【点评】本题主要考查统计图的选择与制作,阅读资料理清所涉数据是解题的关键.
16.为了传承中华优秀传统文化,某校组织了一次七年级的“汉字听写”大赛,七年级1班学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,同学们把成绩进行整理,得到下列表格:
成绩(分) 50 60 70 80 90 100
人数 2 6 9 18 13 2
(1)七年级1班有 50 名学生;
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
成绩(分) 50 60 70 80 90 100
人数 6 9 7 9 15 4
请你谈谈哪个班的比赛成绩好些,并说明理由.
【分析】(1)根据表格中数据即可得出答案;
(2)选择条形图、折线图,即可解答;
(3)根据中位数和众数以及平均数,即可解答.
【解答】解:(1)2+6+9+18+13+2=50;
故答案为:50;
(2)(任选其一);
(3)七年级1班成绩这组数据的中位数是80,众数是80,80分以上的有33人,
平均分为=78(分);
七年级2班成绩这组数据的中位数是80,众数是90;80分以上的有28人,
平均分为=76(分)
所以七年级1班的成绩较好.
【点评】本题考查了统计图的选择,解决本题的关键是熟记统计图的特点.
17.总务处为合理配置学校的体育器材,委托体育教研组调查了解学生对篮球、羽毛球、乒乓球、踢毽子、跳绳等五项体育活动的喜欢程度.体育教研组随机抽查了部分学生,对同学们最喜欢的体育项目(每人只选一项)进行问卷调查,并将统计数据绘制成如下两幅不完整的统计图.
解答下列问题:
(1)填空:m= 20 %,这次问卷调查共抽取了 50 名学生进行调查.
(2)补全图2中的条形统计图.
(3)若全校共有1800名学生,则该校约有多少名学生喜爱打篮球?
【分析】(1)由扇形统计图的知识,可求得m的值,继而求得抽取了的学生数,
(2)总数减去其它即可得乒乓球人数,可补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案;
【解答】解:(1)∵m%=1﹣14%﹣8%﹣24%﹣34%=20%,
∴m=20,
∵喜欢跳绳的占8%,有4人,
∴4÷8%=50(名),
∴共抽取了50名学生;
故答案为:20,50;
(2))喜欢乒乓球的:50×20%=10(名),
条形统计图如图所示;
(3)∵1800×24%=432,
∴该校约有432名学生喜爱打篮球.
【点评】本题考查了条形统计图,观察条形统计图、扇形统计图获得有效信息是解题关键.
18.某中学为了了解本校学生对球类运动的爱好情况,采用抽样的方法,从乒乓球、羽毛球、篮球和排球四个方面抽查了若干名学生,在还没有绘制成功的“折线统计图”与“扇形统计图”中,请你根据已提供的部分信息解答下列问题.
(1)在这次调查活动中,一共调查了 300 名学生;
(2)通过计算,“排球”所在扇形的圆心角是多少度?
(3)请补全折线统计图;
(4)若该校有学生1300名,估计爱好篮球活动的约有多少名学生?
【分析】(1)根据羽毛球的人数和所占的百分比即可求出调查的学生数;
(2)根据圆心角=百分比×360°,计算即可;
(3)求出乒乓球、排球的人数即可解决问题;
(4)用样本估计总体的思想解决问题即可;
【解答】解:(1)本次调查学生人数为:90÷30%=300(名);
故答案为:300;
(2)由图可知,篮球人数为60,
乒乓球人数是300×40%=120,
则排球人数为300﹣60﹣90﹣120=30;
则排球所在的扇形圆心角是×360°=36°;
(3)折线统计图如图所示,
(4)1300×=260(名)
答:若该校有学生1300名,估计爱好篮球活动的约有260名学生.
【点评】本题考查学生的读图能力以及频率、频数的计算.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
19.诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 成绩分组(单位:分) 频数
A 50≤x<60 40
B 60≤x<70 a
C 70≤x<80 90
D 80≤x<90 b
E 90≤x<100 100
合计 c
根据以上信息解答下列问题:
(1)统计表中a= 70 ,b= 200 ,c= 500 ;
(2)扇形统计图中,m的值为 14 ,“E”所对应的圆心角的度数是 72 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?
【分析】(1)根据统计图中的数据可以分别求得a、b、c的值;
(2)根据统计图中的数据可以求得m和“E”所对应的圆心角的度数;
(3)根据题意可以求得成绩在80分及以上的学生大约有多少人.
【解答】解:(1)a=(40÷8%)×(1﹣8%﹣18%﹣40%﹣20%)=70,
b=(40÷8%)×40%=200,
c=40÷8%=500,
故答案为:70,200,500;
(2)m%=1﹣8%﹣18%﹣40%﹣20%=14%,
“E”所对应的圆心角的度数是:360°×20%=72°,
故答案为:14,72;
(3)4000×(40%+20%)=2400(人),
答:成绩在80分及以上的学生大约有2400人.
【点评】本题考查扇形统计图、用样本估计总体、频数分布表,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
