函数的单调性
图片预览


文档简介
函数的单调性
教学目的:理解函数单调性概念,掌握判断函数单调性的方法,会证明一些简单函数在某个区间上的单调性。
教学重点:函数单调性的概念与判断
教学过程:
一、问题情境
1.情境:第2.1.1开头的第三个问题中,θ=f(t)
2.问题:说出气温在哪些时间段内是升高的?怎样用数学语言刻画“随着时间的增大气温逐步升高”这一特征?
二、学生活动
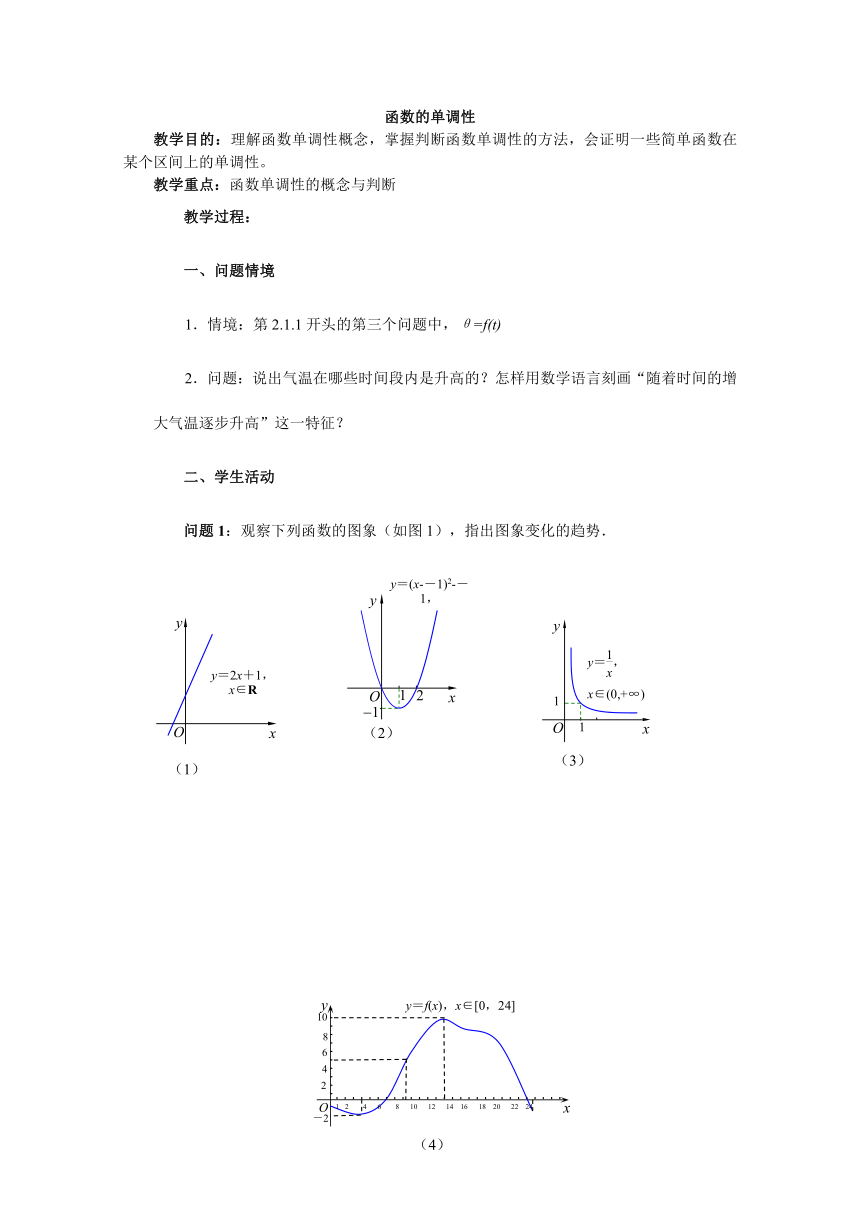
问题1:观察下列函数的图象(如图1),指出图象变化的趋势.
观察得到:随着x值的增大,函数的函数图象 ( http: / / www.21cnjy.com )有的呈逐渐上升的趋势,有的呈逐渐下降的趋势,有的在一个区间内呈上升的趋势,在另一区间内呈逐渐下降的趋势.
问题2:你能明确说出“图象呈逐渐上升趋势”的意思吗?
讨论得到:
在某一区间内,
当x的值增大时,函数值y也增大图象在该区间内呈上升趋势;
当x的值增大时,函数值y反而减小图象在该区间内呈下降趋势。
函数的这种性质称为函数的单调性。
三、建构数学
问题3:如何用数学语言来准确地表述函数的单调性呢?
例如,怎样表述在区间(0,+)上当x的值增大时,函数y的值也增大?
能不能说,由于x=1时,y=3;x=2时,y=5就说随着x的增大,函数值y也随着增大?
能不能说,由于x=1,2,3,4,5,…时,相应地y=3,5,7,9,…就说随着x的增大,函数值y也随着增大?
答案是否定的。
例如函数y=(x--1)2--1(x∈R) ( http: / / www.21cnjy.com ),当x=1,2,3,4,5,…时,相应地y=-1,0,3,8,15,…,就不能说随着x的增大,函数值y也随着增大.这是因为x=-1时,y=3,就自变量的值而言,-1<1,而相应的函数值却有3>-1,即y不是随着x的增大而增大.
通过讨论,结合图(2)给出f(x)在区间I上是单调增函数的定义。
从图1中可以看出:
函数y=2x+1(x∈R)的单调增区间是(-,+);
函数y=(x-1)2-1(xR)的单调增区间是[1,+;
气温曲线所表示的函数的单调增区间是[4,14]。
问题4:如何定义单调减函数?(结合图(3)叙述)
(学生讨论回答)
从图1中可以看出:
函数y=(x-1)2-1(xR)的单调减区间是(-,1];
气温曲线所表示的函数的单调减区间是[0,4],[14,24]。
如果函数y=f(x)在某个区间上是增函数或 ( http: / / www.21cnjy.com )减函数,那么就说函数y=f(x)在这个区间上具有单调性,这个区间就叫做函数y=f(x)的单调区间。
如函数y=2x+1(x∈R)的单调区间是(-,+),函数y=(x-1)2-1(xR)的单调区间是(-,1]和[1,+,气温曲线所表示的函数的单调区间是[0,4],[4,14],[14,24]。
四、数学运用
1.例题
例1 作出下列函数的图象,并写出函数的单调区间.
(1)y=-x 2+2; (2)y=(x≠0).
解 (1)函数y=-x2+2的图像如图4(1)所示,单调减区间为( ∞,0],单调减区间为[0,+∞].
(2)函数y=(x≠0)的图像如图4(2)所示,(-∞,0)和(0,+∞)是两个单调减区间.
提问:能不能说,函数y=(x≠0)在定义域(-∞,0)(0,+∞)上是单调减函数?
引导讨论,从图象上观察或取特殊值代入验证否定结论。(如取x1=-1,x2=).
观察下列函数的图象(如图5),并指出它们是否为定义域上的增函数:
学生总结:函数y=(x-1 ( http: / / www.21cnjy.com ))2与y=|x-1|-1的图象在x≥1时随着x值的增大而上升,在x≤1时随着x的值的增大而下降.所以,这两个函数在定义域上不是增函数.
例3 证明函数f(x)=--1在区间(-∞,0)上是增函数.
证明 设 x1<x2<0,则x1-x2<0且x1x2>0.因为 f(x1)-f(x2)=(--1)-(--1)=-=<0,即f(x1)<f(x2),所以,函数f(x)=--1在区间(-∞,0)上是增函数.
2.练习
课后练习第1、第2、第5题。
五、回顾小结
本节课主要学习了函数单调性的概念以及判断函数在某个区间上的单调性的方法.
六、课外作业
习题2.3:第1题、第2题、第4题、第8题。
(2)
y
x
O
y=(x--1)2--1,
x∈R
1
1
2
y
x
O
y=eq \f(1,x),
x∈(0,+∞)
1
(3)
1
(1)
y
x
O
y=2x+1,
x∈R
(4)
y
x
O
y=f(x),x∈[0,24]
1 2 4 6 8 10 12 14 16 18 20 22 24
2
4
6
8
10
-2
图1
o 1
y
x
y=x3
图-2
图3
y
x
y=f(x)
f(x1)
f(x2)
图2
y
y=f(x)
f(x1)
f(x2)
x
(2)
y
x
O
y = eq \f(1,x) (x≠0)
1
1
图4
(1)
y
x
O
y=x2 1
1
1
2
图5
o 1
x
y
y=(x-1)2
y
o
-1
x
1
y=|x-1|-1
教学目的:理解函数单调性概念,掌握判断函数单调性的方法,会证明一些简单函数在某个区间上的单调性。
教学重点:函数单调性的概念与判断
教学过程:
一、问题情境
1.情境:第2.1.1开头的第三个问题中,θ=f(t)
2.问题:说出气温在哪些时间段内是升高的?怎样用数学语言刻画“随着时间的增大气温逐步升高”这一特征?
二、学生活动
问题1:观察下列函数的图象(如图1),指出图象变化的趋势.
观察得到:随着x值的增大,函数的函数图象 ( http: / / www.21cnjy.com )有的呈逐渐上升的趋势,有的呈逐渐下降的趋势,有的在一个区间内呈上升的趋势,在另一区间内呈逐渐下降的趋势.
问题2:你能明确说出“图象呈逐渐上升趋势”的意思吗?
讨论得到:
在某一区间内,
当x的值增大时,函数值y也增大图象在该区间内呈上升趋势;
当x的值增大时,函数值y反而减小图象在该区间内呈下降趋势。
函数的这种性质称为函数的单调性。
三、建构数学
问题3:如何用数学语言来准确地表述函数的单调性呢?
例如,怎样表述在区间(0,+)上当x的值增大时,函数y的值也增大?
能不能说,由于x=1时,y=3;x=2时,y=5就说随着x的增大,函数值y也随着增大?
能不能说,由于x=1,2,3,4,5,…时,相应地y=3,5,7,9,…就说随着x的增大,函数值y也随着增大?
答案是否定的。
例如函数y=(x--1)2--1(x∈R) ( http: / / www.21cnjy.com ),当x=1,2,3,4,5,…时,相应地y=-1,0,3,8,15,…,就不能说随着x的增大,函数值y也随着增大.这是因为x=-1时,y=3,就自变量的值而言,-1<1,而相应的函数值却有3>-1,即y不是随着x的增大而增大.
通过讨论,结合图(2)给出f(x)在区间I上是单调增函数的定义。
从图1中可以看出:
函数y=2x+1(x∈R)的单调增区间是(-,+);
函数y=(x-1)2-1(xR)的单调增区间是[1,+;
气温曲线所表示的函数的单调增区间是[4,14]。
问题4:如何定义单调减函数?(结合图(3)叙述)
(学生讨论回答)
从图1中可以看出:
函数y=(x-1)2-1(xR)的单调减区间是(-,1];
气温曲线所表示的函数的单调减区间是[0,4],[14,24]。
如果函数y=f(x)在某个区间上是增函数或 ( http: / / www.21cnjy.com )减函数,那么就说函数y=f(x)在这个区间上具有单调性,这个区间就叫做函数y=f(x)的单调区间。
如函数y=2x+1(x∈R)的单调区间是(-,+),函数y=(x-1)2-1(xR)的单调区间是(-,1]和[1,+,气温曲线所表示的函数的单调区间是[0,4],[4,14],[14,24]。
四、数学运用
1.例题
例1 作出下列函数的图象,并写出函数的单调区间.
(1)y=-x 2+2; (2)y=(x≠0).
解 (1)函数y=-x2+2的图像如图4(1)所示,单调减区间为( ∞,0],单调减区间为[0,+∞].
(2)函数y=(x≠0)的图像如图4(2)所示,(-∞,0)和(0,+∞)是两个单调减区间.
提问:能不能说,函数y=(x≠0)在定义域(-∞,0)(0,+∞)上是单调减函数?
引导讨论,从图象上观察或取特殊值代入验证否定结论。(如取x1=-1,x2=).
观察下列函数的图象(如图5),并指出它们是否为定义域上的增函数:
学生总结:函数y=(x-1 ( http: / / www.21cnjy.com ))2与y=|x-1|-1的图象在x≥1时随着x值的增大而上升,在x≤1时随着x的值的增大而下降.所以,这两个函数在定义域上不是增函数.
例3 证明函数f(x)=--1在区间(-∞,0)上是增函数.
证明 设 x1<x2<0,则x1-x2<0且x1x2>0.因为 f(x1)-f(x2)=(--1)-(--1)=-=<0,即f(x1)<f(x2),所以,函数f(x)=--1在区间(-∞,0)上是增函数.
2.练习
课后练习第1、第2、第5题。
五、回顾小结
本节课主要学习了函数单调性的概念以及判断函数在某个区间上的单调性的方法.
六、课外作业
习题2.3:第1题、第2题、第4题、第8题。
(2)
y
x
O
y=(x--1)2--1,
x∈R
1
1
2
y
x
O
y=eq \f(1,x),
x∈(0,+∞)
1
(3)
1
(1)
y
x
O
y=2x+1,
x∈R
(4)
y
x
O
y=f(x),x∈[0,24]
1 2 4 6 8 10 12 14 16 18 20 22 24
2
4
6
8
10
-2
图1
o 1
y
x
y=x3
图-2
图3
y
x
y=f(x)
f(x1)
f(x2)
图2
y
y=f(x)
f(x1)
f(x2)
x
(2)
y
x
O
y = eq \f(1,x) (x≠0)
1
1
图4
(1)
y
x
O
y=x2 1
1
1
2
图5
o 1
x
y
y=(x-1)2
y
o
-1
x
1
y=|x-1|-1
