圆的有关性质华东师大版)[上学期]
文档属性
| 名称 | 圆的有关性质华东师大版)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 226.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-24 00:00:00 | ||
图片预览





文档简介
课件13张PPT。圆的有关性质 授课老师:黄安锦考试要求1. 理解圆及其有关概念,了解弧、弦、圆心角的关系.2.探索圆的性质,了解圆周角
与圆心角的关系。3.了解三角形的内心和外心。知识与方法1.与圆有关的概念:
(1)弦:
(2)直径:
(3)弧:
(4)优弧:
(5)劣弧:
(6)等弧:
(7)半圆:
(8)等圆:连结圆上任意两点的线段.经过圆心的弦.圆上任意两点间的部分.在同圆或等圆中,能够完全重合的弧.大于半圆周的圆弧。小于半圆周的圆弧。圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。半径相等的两个圆叫做等圆。3、在同一个圆中,弦、弧、圆心角三者之间的关系?在一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。2.定理:不在同一直线上的三个点确定一个圆.知识与方法4.圆心角与圆周角的关系?在同一圆内,同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半。
相等的圆周角所对的弧相等。7、三角形的外心、内心的性质?5、半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.知识与方法解题技巧6、垂直于弦的直径性质:垂直于弦的直径平分弦,
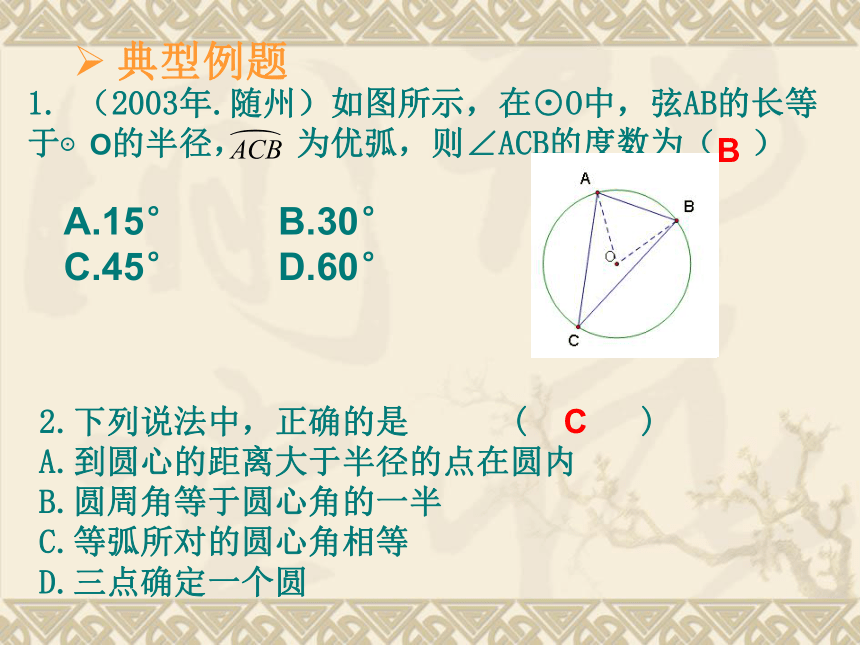
并且平分弦所对的两条弧.由于圆的知识具有综合性,常常需要巧妙地添加辅助线,将圆的问题转化成特殊的三角形、四边形。典型例题B1. (2003年.随州)如图所示,在⊙O中,弦AB的长等于⊙O的半径, 为优弧,则∠ACB的度数为( ) A.15° B.30°
C.45° D.60°2.下列说法中,正确的是 ( )
A.到圆心的距离大于半径的点在圆内
B.圆周角等于圆心角的一半
C.等弧所对的圆心角相等
D.三点确定一个圆C典型例题3.(2003年,辽宁)如图,AB是⊙O直径,弦CD ⊥AB于E,若AB=9,BE=1,则CD= 。与圆有关的“双解”题1、已知⊙O和一点P,在点P与⊙O上的各点连结的线
段中,最长的为4cm,最短的为2cm,求⊙O的半径。解: ⊙O的半径依据点P位置
的不同而有两个结果
(1)点P在⊙O外时,
作直线PO,分别交⊙O
于A、B两点。此时,
PB最长为4cm,PA最短为2cm, ⊙O的半径为1cm(2)点P在⊙O内时,作直线PO,分别交⊙O于A、
B两点,此时,PB最长为4cm,PA最短为2cm,
⊙O的半径为3cm.所以⊙O的半径为3cm或1cm.2、(05年淮安)如果点O为△ABC的外心,
∠BOC= 70°,那么 ∠BAC= .35°能力检测1、如图,P为⊙O的直径AB上一点,PC⊥AB,PC交
⊙O于C, ∠OCP的平分钱交⊙O于D。当点P在半径
OA(不包括O点和A点)上移动时,试比较
的大小,并说明理由。2、如图,△ABC内接于⊙O,延长BC边上的高AD
交⊙O于F,连结CF,作弦BE=CF,再连结AE,
试说明AE为⊙O的直径。能力检测能力检测3、如图,AB为⊙O的直径,CD为⊙O的弦,AB、CD
的延长线交于E,已知AB=2DE,∠E=180,则∠AOC
的度数为 。方法小结:1..
2.遇直径条件时,常构造直径所对的圆周角,得到90°
的角.
与圆心角的关系。3.了解三角形的内心和外心。知识与方法1.与圆有关的概念:
(1)弦:
(2)直径:
(3)弧:
(4)优弧:
(5)劣弧:
(6)等弧:
(7)半圆:
(8)等圆:连结圆上任意两点的线段.经过圆心的弦.圆上任意两点间的部分.在同圆或等圆中,能够完全重合的弧.大于半圆周的圆弧。小于半圆周的圆弧。圆的任意一条直径的两个端点分圆成两条弧,每一条弧都叫做半圆。半径相等的两个圆叫做等圆。3、在同一个圆中,弦、弧、圆心角三者之间的关系?在一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。2.定理:不在同一直线上的三个点确定一个圆.知识与方法4.圆心角与圆周角的关系?在同一圆内,同弧或等弧所对的圆周角相等,
都等于该弧所对的圆心角的一半。
相等的圆周角所对的弧相等。7、三角形的外心、内心的性质?5、半圆(或直径)所对的圆周角是直角;
90°的圆周角所对的弦是直径.知识与方法解题技巧6、垂直于弦的直径性质:垂直于弦的直径平分弦,
并且平分弦所对的两条弧.由于圆的知识具有综合性,常常需要巧妙地添加辅助线,将圆的问题转化成特殊的三角形、四边形。典型例题B1. (2003年.随州)如图所示,在⊙O中,弦AB的长等于⊙O的半径, 为优弧,则∠ACB的度数为( ) A.15° B.30°
C.45° D.60°2.下列说法中,正确的是 ( )
A.到圆心的距离大于半径的点在圆内
B.圆周角等于圆心角的一半
C.等弧所对的圆心角相等
D.三点确定一个圆C典型例题3.(2003年,辽宁)如图,AB是⊙O直径,弦CD ⊥AB于E,若AB=9,BE=1,则CD= 。与圆有关的“双解”题1、已知⊙O和一点P,在点P与⊙O上的各点连结的线
段中,最长的为4cm,最短的为2cm,求⊙O的半径。解: ⊙O的半径依据点P位置
的不同而有两个结果
(1)点P在⊙O外时,
作直线PO,分别交⊙O
于A、B两点。此时,
PB最长为4cm,PA最短为2cm, ⊙O的半径为1cm(2)点P在⊙O内时,作直线PO,分别交⊙O于A、
B两点,此时,PB最长为4cm,PA最短为2cm,
⊙O的半径为3cm.所以⊙O的半径为3cm或1cm.2、(05年淮安)如果点O为△ABC的外心,
∠BOC= 70°,那么 ∠BAC= .35°能力检测1、如图,P为⊙O的直径AB上一点,PC⊥AB,PC交
⊙O于C, ∠OCP的平分钱交⊙O于D。当点P在半径
OA(不包括O点和A点)上移动时,试比较
的大小,并说明理由。2、如图,△ABC内接于⊙O,延长BC边上的高AD
交⊙O于F,连结CF,作弦BE=CF,再连结AE,
试说明AE为⊙O的直径。能力检测能力检测3、如图,AB为⊙O的直径,CD为⊙O的弦,AB、CD
的延长线交于E,已知AB=2DE,∠E=180,则∠AOC
的度数为 。方法小结:1..
2.遇直径条件时,常构造直径所对的圆周角,得到90°
的角.
