【2023版】人教版数学八上-第11章 三角形 11.2.2 三角形的外角 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第11章 三角形 11.2.2 三角形的外角 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览






文档简介
(共24张PPT)
11.2.2 三角形的外角
第十一章 三角形
必
●
知识要点全练
夯实基础
000000000000000000000000000000000000
知识点1三角形的外角概念
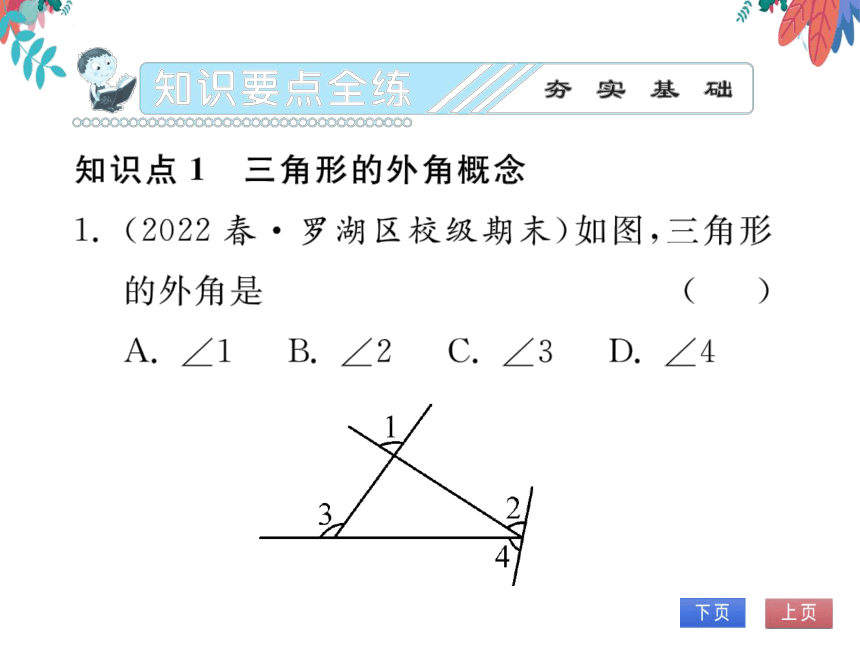
1.(2022春·罗湖区校级期末)如图,三角形
的外角是
(C)
A.∠1
B.
∠2
C.∠3
D.∠4
3
2<
4
(第1题图)
知识点2三角形的外角性质及应用
2.(湖南湘潭中芳)如图,∠ACD是△ABC的
外角,若∠ACD=110°,∠B=50°,则∠A
的度数为
(D)
A.40°
B.
509
C.55°
D.
609
A
B
C
D
(第2题图)
3.(2021·陕西)如图,点D、E分别在线段BC、
AC上,连接AD、BE.若∠A=35°,∠B=25°,
∠C=50°,则∠1的大小为
B
A.60°
B.70°
C.75
D.85°
A
1
E
B
D
(第3题图)
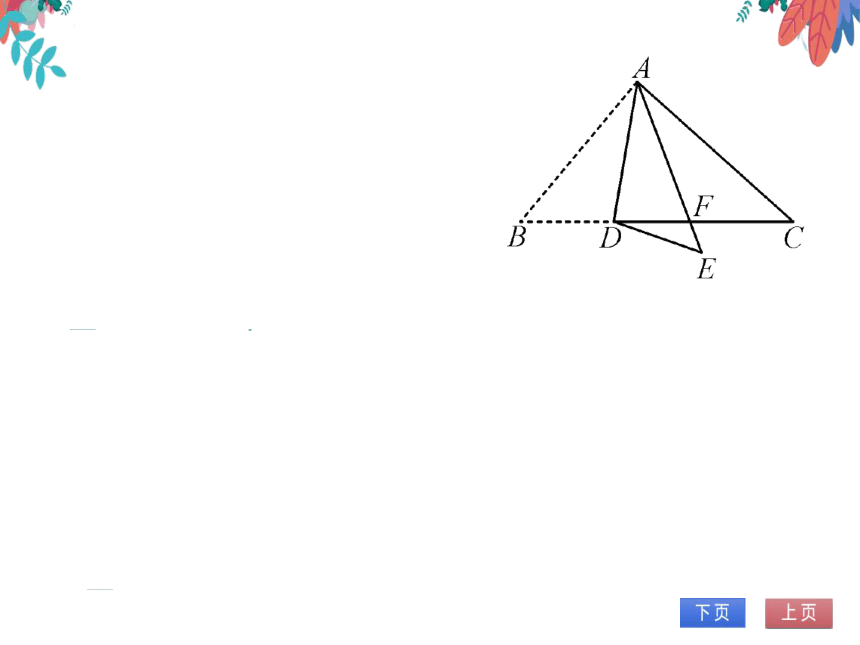
4.(2022春·准阳区期末)如图,在△ABC
中,点D是BC边上的一点,∠B=50°,
∠BAD=30°,将△ABD沿AD折叠得到
△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.
解:(1).·△ABD沿AD折叠得
到△AED,.∠BAD=∠DAF,
.∠B=50°,∠BAD=30°,
F
.∠AFC=∠B十∠BAD十
B
E
∠DAF=110°;
(2).∠B=50°,∠BAD=30°,./ADB=180°一50°一30
=100°,∠ADC=50°十30°=80°,°△ABD沿AD折叠得
到△AED,..∠ADE=∠ADB=100°,.∠EDF=∠ADE
-∠ADC=100°-80°=20°.
5.(2022春·长安区期中)小红同学以“一个
含30°的直角三角尺和两条平行线”为背景
开展探究活动.如图,在直角三角形ABC
中,已知∠BAC=90°,∠ABC=30°,
∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过
点C),若∠1=43°,求∠2的度数;
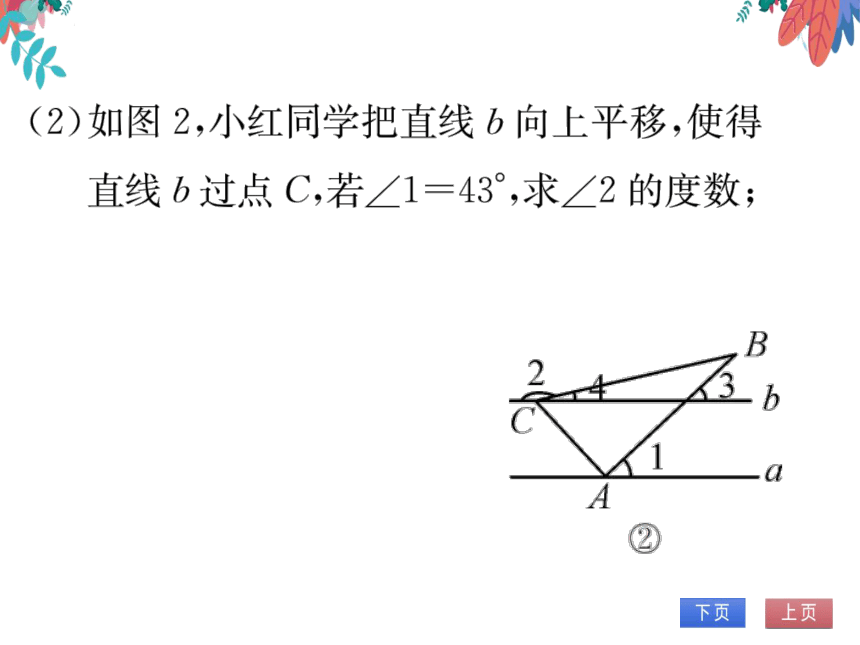
(2)如图2,小红同学把直线b向上平移,使得
直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平
移,使得直线b与线段BC相交(b不过
点B),设∠1=x(30°≤x≤90),∠2=
y,求y与x之间的关系式.
11.2.2 三角形的外角
第十一章 三角形
必
●
知识要点全练
夯实基础
000000000000000000000000000000000000
知识点1三角形的外角概念
1.(2022春·罗湖区校级期末)如图,三角形
的外角是
(C)
A.∠1
B.
∠2
C.∠3
D.∠4
3
2<
4
(第1题图)
知识点2三角形的外角性质及应用
2.(湖南湘潭中芳)如图,∠ACD是△ABC的
外角,若∠ACD=110°,∠B=50°,则∠A
的度数为
(D)
A.40°
B.
509
C.55°
D.
609
A
B
C
D
(第2题图)
3.(2021·陕西)如图,点D、E分别在线段BC、
AC上,连接AD、BE.若∠A=35°,∠B=25°,
∠C=50°,则∠1的大小为
B
A.60°
B.70°
C.75
D.85°
A
1
E
B
D
(第3题图)
4.(2022春·准阳区期末)如图,在△ABC
中,点D是BC边上的一点,∠B=50°,
∠BAD=30°,将△ABD沿AD折叠得到
△AED,AE与BC交于点F.
(1)求∠AFC的度数;
(2)求∠EDF的度数.
解:(1).·△ABD沿AD折叠得
到△AED,.∠BAD=∠DAF,
.∠B=50°,∠BAD=30°,
F
.∠AFC=∠B十∠BAD十
B
E
∠DAF=110°;
(2).∠B=50°,∠BAD=30°,./ADB=180°一50°一30
=100°,∠ADC=50°十30°=80°,°△ABD沿AD折叠得
到△AED,..∠ADE=∠ADB=100°,.∠EDF=∠ADE
-∠ADC=100°-80°=20°.
5.(2022春·长安区期中)小红同学以“一个
含30°的直角三角尺和两条平行线”为背景
开展探究活动.如图,在直角三角形ABC
中,已知∠BAC=90°,∠ABC=30°,
∠ACB=60°,直线a∥b.
(1)如图1,直线b与线段AC相交(b不过
点C),若∠1=43°,求∠2的度数;
(2)如图2,小红同学把直线b向上平移,使得
直线b过点C,若∠1=43°,求∠2的度数;
(3)如用3,小红同学把直线b继续向上平
移,使得直线b与线段BC相交(b不过
点B),设∠1=x(30°≤x≤90),∠2=
y,求y与x之间的关系式.
