【2023版】人教版数学八上-第11章 三角形 专题训练(一)与三角形的边和角有关的计算 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第11章 三角形 专题训练(一)与三角形的边和角有关的计算 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览



文档简介
(共23张PPT)
专题训练(一) 与三角形的边和
角有关的计算
第十一章 三角形
必
●
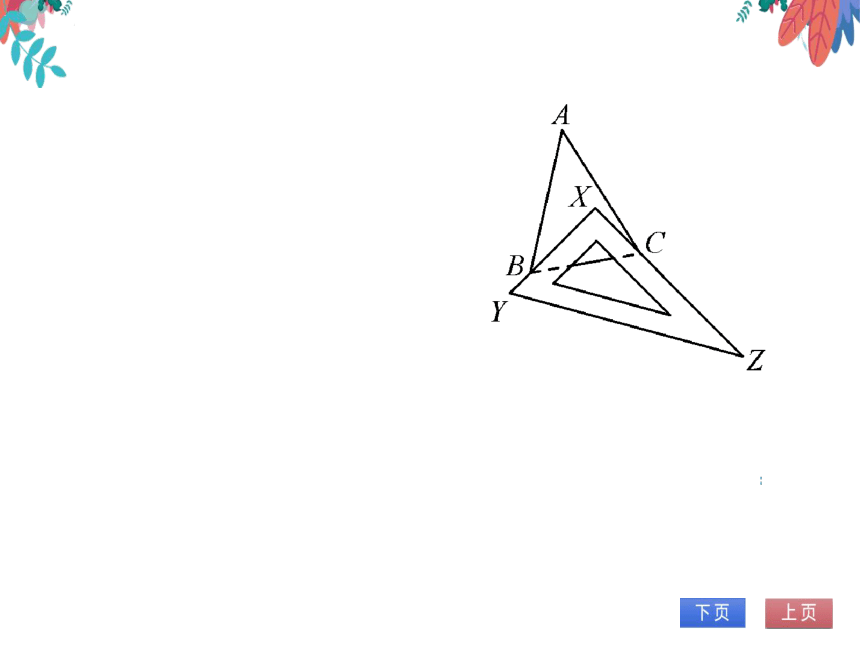
1.如图,有一块含30°角的三角尺XYZ放置
在△ABC上,三角尺的两条直角边XY和
XZ恰好分别经过点B和点C.
(1)若∠A=45°,求∠ABX+∠ACX的度数;
(2)若改变三角尺的位置,但仍使点B,C分
别在三角尺的边XY和XZ上,此时
∠ABX十∠ACX的度数有变化吗?请
说明理由.
解:(1),∠A=45°,
,。∠ABC十∠ACB=180°一/A=
180°一45=135°.
.'∠YXZ=90°,
.∠XBC+∠XCB=180°一∠YXZ
Z
=180°一90°=90°.
·'.∠ABX+∠ACX=(∠ABC+∠ACB)一(∠XBC+∠XCB)=
135°一90°=45.
(2)∠ABX十∠ACX的度数没有变化.理由如下:
.∠YXZ=90°,
.∠XBC+∠XCB=180°-∠YXZ=180°-90°=90°.
又∠ABC+∠ACB=180°-∠A,
'.∠ABX+∠ACX=(∠ABC+∠ACB)一(∠XBC+∠XCB)=
180°一∠A-90°=90°-∠A,
即∠ABX十∠ACX的度数没有变化.
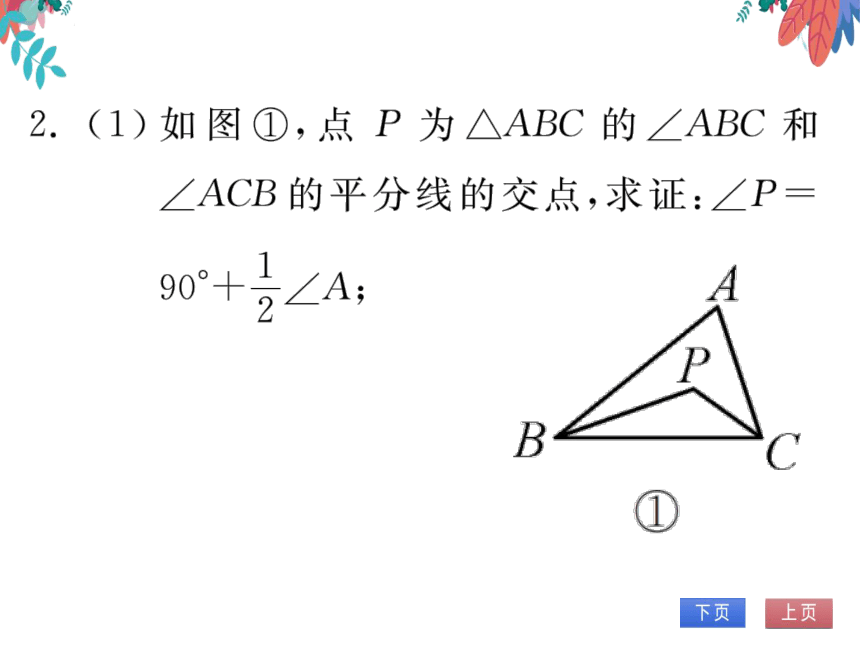
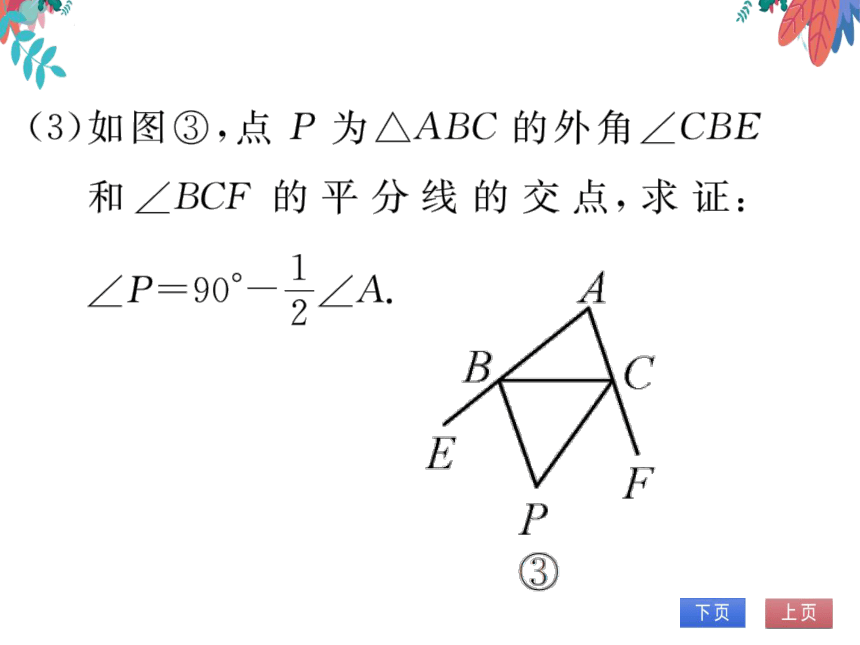
2.(1)如图①,点P为△ABC的∠ABC和
∠ACB的平分线的交点,求证:∠P=
90+7∠A:
P
B
C
①
证明:I)∠P-I80-(∠PC+∠PB)=I80-3(∠AC
+∠ACB)=180-2(180°-∠A)=90+号∠A.
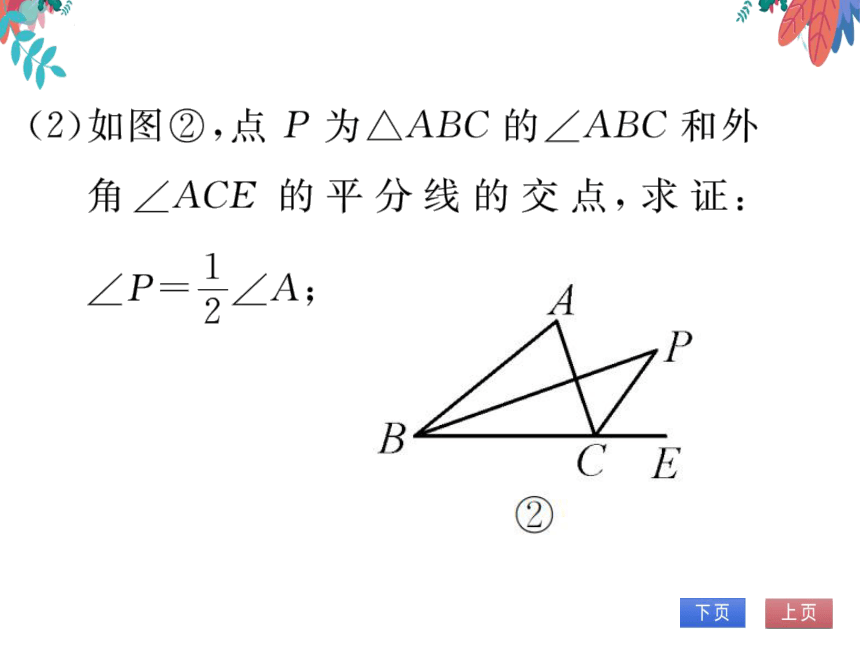
(2)∠P-∠B-∠PBE=(∠AE-∠ABC=号∠A.
(3)∠P=180-(∠PBC+∠PCB)=180°-?(∠EBC+
∠FCB)=180-号(∠A+∠ACB+∠CB)=180-
(∠A+180)=90°-3∠A.
2
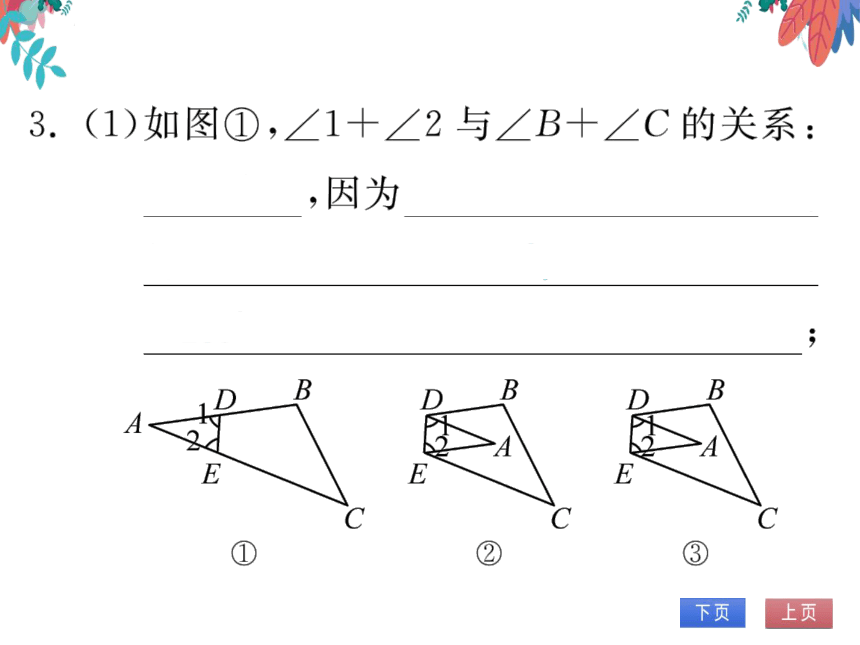
3.(1)如图①,∠1十∠2与∠B十C的关系:
相等,因为
由三角形内角和定理
得∠1十∠2+∠A=180°,∠B+∠C+/A
=180°
B
B
B
E
E
E
①
②
③
(2)把图①中的△ABC沿DE折叠,得到图
②,则∠1+∠2
=(填“>”“<”或
“=”)∠B十∠C.当∠A=40°时,
/1+
∠2+∠B十∠C=
280°
(3)如图③,将图①中的△ABC沿DE折
叠,如果∠A=30°,则∠BDA十∠CEA=
360°-(∠B+∠C+∠1+∠2)=360°
300°
60°.猜想∠BDA+
∠CEA与∠A的关系为
∠BDA+
∠
CEA=2∠A
专题训练(一) 与三角形的边和
角有关的计算
第十一章 三角形
必
●
1.如图,有一块含30°角的三角尺XYZ放置
在△ABC上,三角尺的两条直角边XY和
XZ恰好分别经过点B和点C.
(1)若∠A=45°,求∠ABX+∠ACX的度数;
(2)若改变三角尺的位置,但仍使点B,C分
别在三角尺的边XY和XZ上,此时
∠ABX十∠ACX的度数有变化吗?请
说明理由.
解:(1),∠A=45°,
,。∠ABC十∠ACB=180°一/A=
180°一45=135°.
.'∠YXZ=90°,
.∠XBC+∠XCB=180°一∠YXZ
Z
=180°一90°=90°.
·'.∠ABX+∠ACX=(∠ABC+∠ACB)一(∠XBC+∠XCB)=
135°一90°=45.
(2)∠ABX十∠ACX的度数没有变化.理由如下:
.∠YXZ=90°,
.∠XBC+∠XCB=180°-∠YXZ=180°-90°=90°.
又∠ABC+∠ACB=180°-∠A,
'.∠ABX+∠ACX=(∠ABC+∠ACB)一(∠XBC+∠XCB)=
180°一∠A-90°=90°-∠A,
即∠ABX十∠ACX的度数没有变化.
2.(1)如图①,点P为△ABC的∠ABC和
∠ACB的平分线的交点,求证:∠P=
90+7∠A:
P
B
C
①
证明:I)∠P-I80-(∠PC+∠PB)=I80-3(∠AC
+∠ACB)=180-2(180°-∠A)=90+号∠A.
(2)∠P-∠B-∠PBE=(∠AE-∠ABC=号∠A.
(3)∠P=180-(∠PBC+∠PCB)=180°-?(∠EBC+
∠FCB)=180-号(∠A+∠ACB+∠CB)=180-
(∠A+180)=90°-3∠A.
2
3.(1)如图①,∠1十∠2与∠B十C的关系:
相等,因为
由三角形内角和定理
得∠1十∠2+∠A=180°,∠B+∠C+/A
=180°
B
B
B
E
E
E
①
②
③
(2)把图①中的△ABC沿DE折叠,得到图
②,则∠1+∠2
=(填“>”“<”或
“=”)∠B十∠C.当∠A=40°时,
/1+
∠2+∠B十∠C=
280°
(3)如图③,将图①中的△ABC沿DE折
叠,如果∠A=30°,则∠BDA十∠CEA=
360°-(∠B+∠C+∠1+∠2)=360°
300°
60°.猜想∠BDA+
∠CEA与∠A的关系为
∠BDA+
∠
CEA=2∠A
