【2023版】人教版数学八上-第12章 全等三角形 12.2 第3课时 用“ASA”和“AAS”证三角形全等 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第12章 全等三角形 12.2 第3课时 用“ASA”和“AAS”证三角形全等 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
12.2第3课时 用“ASA”和“AAS”证
三角形全等
第十二章 全等三角形
必
●
知识要点全练
夯实基础
00000000000000000000000000000000000
知识点1
用“ASA”判定三角形全等
1.如图,某同学不小心把一块三
角形玻璃打碎成三块,现在要
3
到玻璃店配一块与原来完全相
同的玻璃,最省事的方法是
A.带①和②去
B.只带②去
C.只带③去
D.都带去
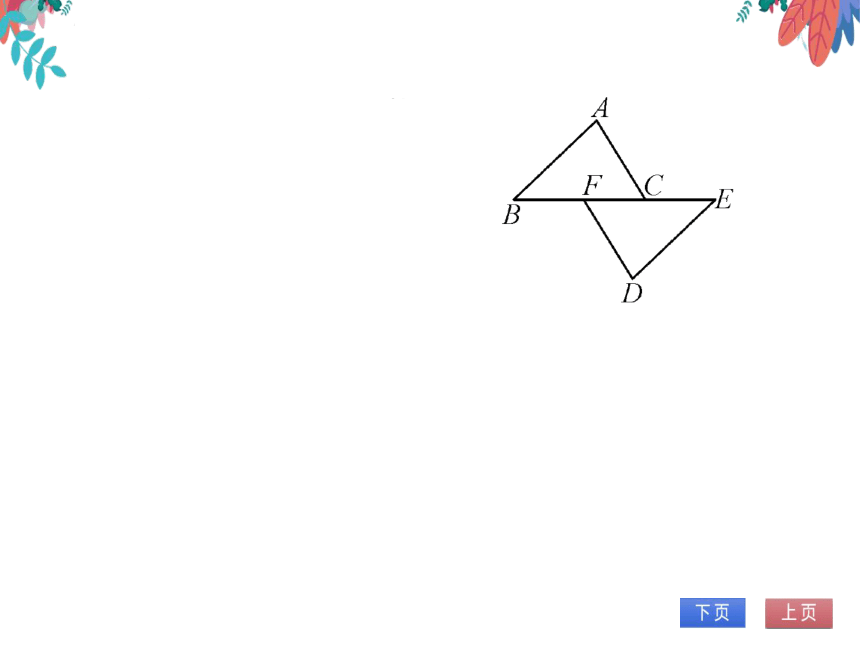
2.(2022春·碑林区期末)在△ABC和
△DEF中,已知∠B=∠E,BF=EC,
AC∥FD.△ABC与△DEF全等吗?为
什么?
解:全等.理由:。AC∥FD,
。∠ACB=∠DFE,,BF
B
E
=EC,..BF+FC=EC十
CF,即BC=EF,在人ABC
∠B=∠E,
和人DEF中,〈BC=EF,
/ACB=∠DFE,
.∧ABC≌△DEF(ASA).
知识点2
用“AAS”判定三角形全等
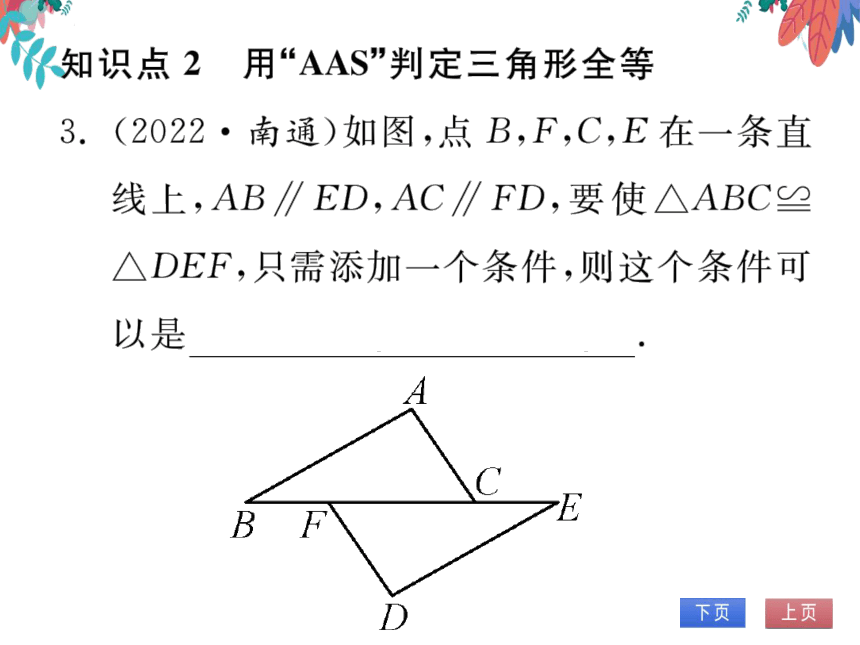
3.(2022·南通)如图,点B,F,C,E在一条直
线上,AB∥ED,AC∥FD,要使△ABC≌
△DEF,只需添加一个条件,则这个条件可
以是
AB=DE(答案不唯一)·
A
C
B F
E
D
(第3题图)
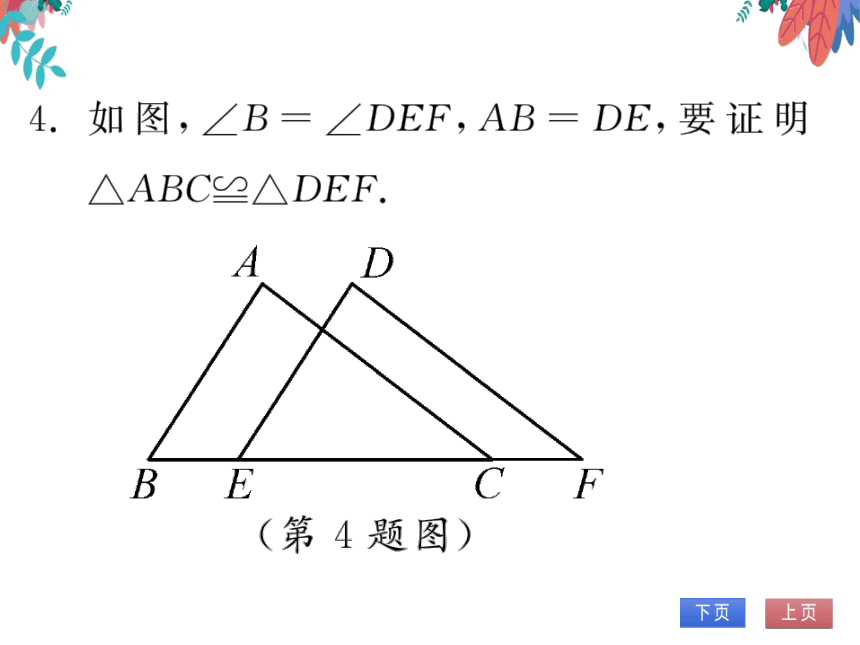
4.如图,∠B=∠DEF,AB=DE,要证明
△ABC≌∧DEF.
(1)若以“SAS”为依据,还需添加的条件为
D
B
E
C
F
(第4题图)
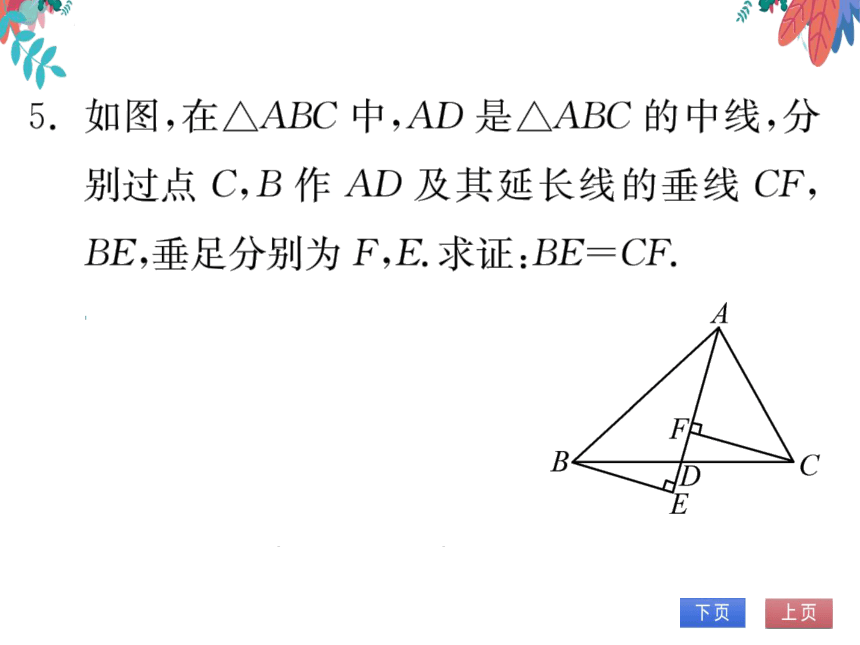
6.(2022春·峡江县期末)如图所示,点E在
△ABC外部,点D在BC边上,DE交AC
于F,若∠1=∠3,∠E=∠C,AE=AC,问
△ABC≌△ADE吗?请说明理由.
解:人ABC和△ADE全等,
E
理由是:,∠ADC=∠B十
∠1=∠3+∠ADE,又.
B
∠1=∠3,.∠B=∠ADE,
∠C=∠E,
在△ABC和人ADE中,{∠B=∠ADE,
AC=AE,
.。△ABC≌△ADE(AAS),即△ABC和
个ADE全等.
规律方法全练
提升能力
o00000000000000000000000000000000000
7.如图,已知AE=CF,∠AFD=∠CEB,那
么添加下列一个条件后,仍无法判定
△ADF≌△CBE的是
(B)
A.∠A=∠C
B.AD
=CB
C.BE=DE
D.AD∥BC
A
D
E
F
B
C
(第7题图)
8.如图,ABCD,且AB=CD,E,F是AD
上两点,CE⊥AD,BF⊥AD.若CE=a,
BF=b,EF=c,则AD的长为
(D)
A.a+c
B.6c
C.a-b+c
D.a+b-c
12.2第3课时 用“ASA”和“AAS”证
三角形全等
第十二章 全等三角形
必
●
知识要点全练
夯实基础
00000000000000000000000000000000000
知识点1
用“ASA”判定三角形全等
1.如图,某同学不小心把一块三
角形玻璃打碎成三块,现在要
3
到玻璃店配一块与原来完全相
同的玻璃,最省事的方法是
A.带①和②去
B.只带②去
C.只带③去
D.都带去
2.(2022春·碑林区期末)在△ABC和
△DEF中,已知∠B=∠E,BF=EC,
AC∥FD.△ABC与△DEF全等吗?为
什么?
解:全等.理由:。AC∥FD,
。∠ACB=∠DFE,,BF
B
E
=EC,..BF+FC=EC十
CF,即BC=EF,在人ABC
∠B=∠E,
和人DEF中,〈BC=EF,
/ACB=∠DFE,
.∧ABC≌△DEF(ASA).
知识点2
用“AAS”判定三角形全等
3.(2022·南通)如图,点B,F,C,E在一条直
线上,AB∥ED,AC∥FD,要使△ABC≌
△DEF,只需添加一个条件,则这个条件可
以是
AB=DE(答案不唯一)·
A
C
B F
E
D
(第3题图)
4.如图,∠B=∠DEF,AB=DE,要证明
△ABC≌∧DEF.
(1)若以“SAS”为依据,还需添加的条件为
D
B
E
C
F
(第4题图)
6.(2022春·峡江县期末)如图所示,点E在
△ABC外部,点D在BC边上,DE交AC
于F,若∠1=∠3,∠E=∠C,AE=AC,问
△ABC≌△ADE吗?请说明理由.
解:人ABC和△ADE全等,
E
理由是:,∠ADC=∠B十
∠1=∠3+∠ADE,又.
B
∠1=∠3,.∠B=∠ADE,
∠C=∠E,
在△ABC和人ADE中,{∠B=∠ADE,
AC=AE,
.。△ABC≌△ADE(AAS),即△ABC和
个ADE全等.
规律方法全练
提升能力
o00000000000000000000000000000000000
7.如图,已知AE=CF,∠AFD=∠CEB,那
么添加下列一个条件后,仍无法判定
△ADF≌△CBE的是
(B)
A.∠A=∠C
B.AD
=CB
C.BE=DE
D.AD∥BC
A
D
E
F
B
C
(第7题图)
8.如图,ABCD,且AB=CD,E,F是AD
上两点,CE⊥AD,BF⊥AD.若CE=a,
BF=b,EF=c,则AD的长为
(D)
A.a+c
B.6c
C.a-b+c
D.a+b-c
