【2023版】人教版数学八上-第12章 全等三角形 12.2 第4课时 用“HL”证两个直角三角形全等 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第12章 全等三角形 12.2 第4课时 用“HL”证两个直角三角形全等 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览



文档简介
(共19张PPT)
12.2第4课时 用“HL”证两个
直角三角形全等
第十二章 全等三角形
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1)
用“HL”判定直角三角形全等
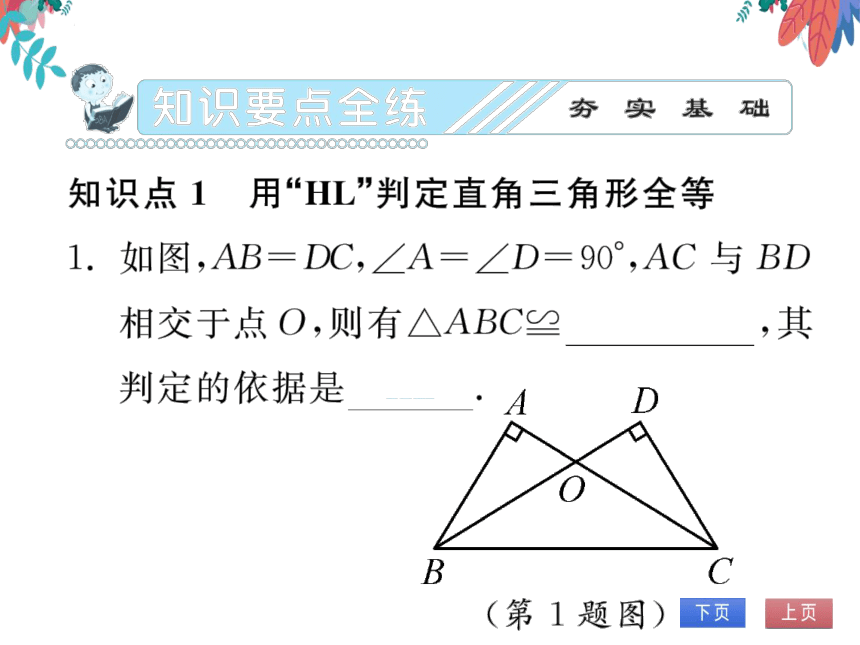
1.如图,AB=DC,∠A=∠D=90°,AC与BD
相交于点O,则有人ABC2
人DCB,其
判定的依据是
HL
D
O
B
C
(第1题图)
2.如图,在△ABC中,∠C=90°,DEAB于
E,BE=BC,如果AC=6,那么AD+DE
等于6
B
E
A
D
C
(第2题图)
知识点2
直角三角形全等的判定方法的灵
活运用
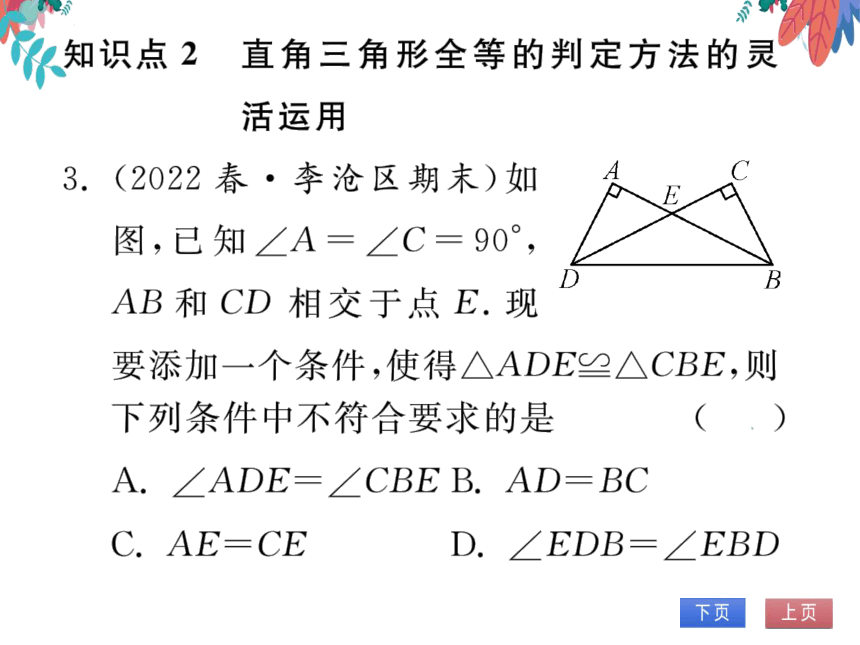
3.(2022春·李沧区期末)如
图,已知∠A=∠C=90°,
B
AB和CD相交于点E.现
要添加一个条件,使得△ADE≌△CBE,则
下列条件中不符合要求的是
(A)
A.∠ADE=∠CBEB.AD=BC
C.AE-CE
D.∠EDB=∠EBD
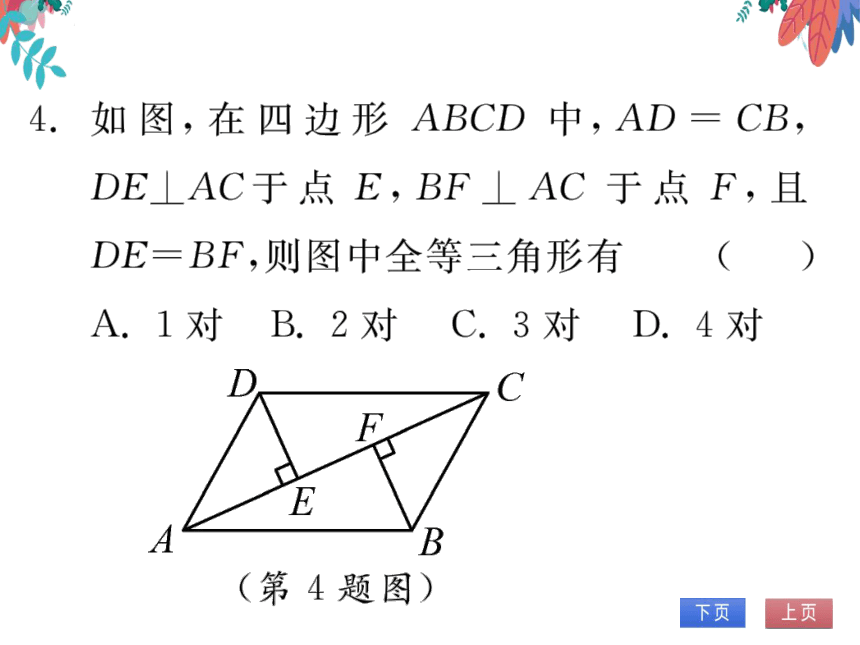
D
C
F
E
A
B
(第4题图)
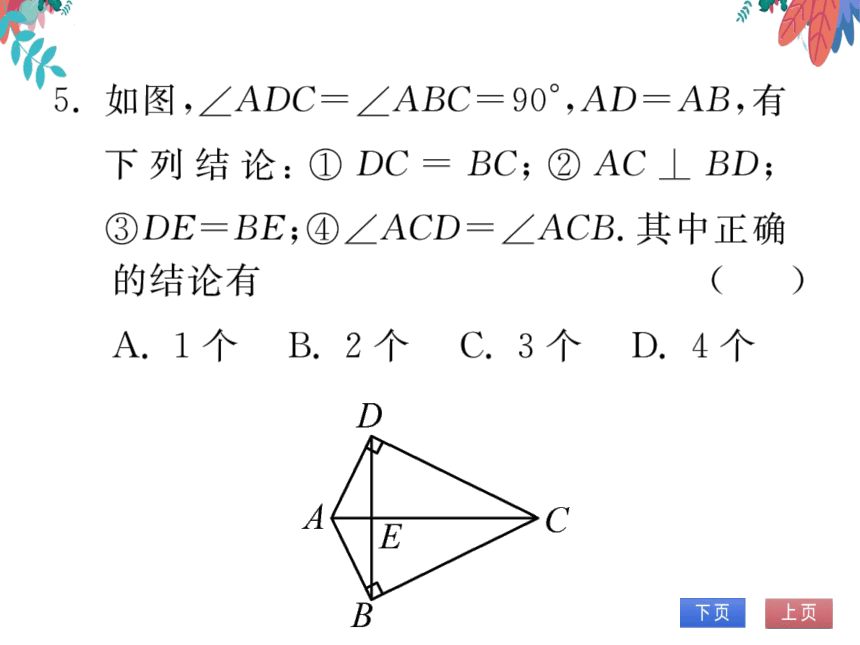
5.
如图,∠ADC=∠ABC=90°,AD=AB,有
下列结论:①DC=BC;②AC⊥BD;
③DE=BE;④∠ACD=∠ACB.其中正确
D
A
E
C
B
(第5题图)
6.如图,在长方形ABCD中,A
AB=4,AD=6.延长BC到
点E,使CE=2,连接DE.
CE
动点P从点B出发,以每秒2个单位的速
度沿B→C→D→A的方向向终点A运动,
设点P的运动时间为t秒,当△ABP和
△DCE全等时,t的值为
(C)
A.1
B.1或3C.1或7D.3或7
7.(2022春·三元区校级月考)已知:如图,点
E、F在线段BD上,AF⊥BD,CEBD,
AD=CB,DE=BF,求证:AF=CE.
证明:。°DE=BF,。。DE十EF=
B
BF十EF,。.DF=BE,
在Rt△ADF和Rt△CBE中,
DF=BE,
AD=CE,
'.Rt∧ADF≌Rt∧CDE(HL)..'.AF=CE.
8.如图,AB=AD,∠ABC=∠ADC=90°,EF过
点C,BE⊥EF于点E,DF⊥EF于点F,BE=
DF,求证:△BCE2△DCF.
证明:连接AC,在Rt△ABC
和Rt△ADC中,
B
.AB=AD,AC=AC,
.'.Rt∧ABC≌Rt入ADC(HI),
E
。。BC=DC,
.BE⊥EF,DF⊥EF,.∠E=∠F=90°.
在Rt△BCE和Rt人DCF中,
BC=DC,
BE=DF,
..Rt人BCE≌RtDCF(HL).
12.2第4课时 用“HL”证两个
直角三角形全等
第十二章 全等三角形
必
●
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1)
用“HL”判定直角三角形全等
1.如图,AB=DC,∠A=∠D=90°,AC与BD
相交于点O,则有人ABC2
人DCB,其
判定的依据是
HL
D
O
B
C
(第1题图)
2.如图,在△ABC中,∠C=90°,DEAB于
E,BE=BC,如果AC=6,那么AD+DE
等于6
B
E
A
D
C
(第2题图)
知识点2
直角三角形全等的判定方法的灵
活运用
3.(2022春·李沧区期末)如
图,已知∠A=∠C=90°,
B
AB和CD相交于点E.现
要添加一个条件,使得△ADE≌△CBE,则
下列条件中不符合要求的是
(A)
A.∠ADE=∠CBEB.AD=BC
C.AE-CE
D.∠EDB=∠EBD
D
C
F
E
A
B
(第4题图)
5.
如图,∠ADC=∠ABC=90°,AD=AB,有
下列结论:①DC=BC;②AC⊥BD;
③DE=BE;④∠ACD=∠ACB.其中正确
D
A
E
C
B
(第5题图)
6.如图,在长方形ABCD中,A
AB=4,AD=6.延长BC到
点E,使CE=2,连接DE.
CE
动点P从点B出发,以每秒2个单位的速
度沿B→C→D→A的方向向终点A运动,
设点P的运动时间为t秒,当△ABP和
△DCE全等时,t的值为
(C)
A.1
B.1或3C.1或7D.3或7
7.(2022春·三元区校级月考)已知:如图,点
E、F在线段BD上,AF⊥BD,CEBD,
AD=CB,DE=BF,求证:AF=CE.
证明:。°DE=BF,。。DE十EF=
B
BF十EF,。.DF=BE,
在Rt△ADF和Rt△CBE中,
DF=BE,
AD=CE,
'.Rt∧ADF≌Rt∧CDE(HL)..'.AF=CE.
8.如图,AB=AD,∠ABC=∠ADC=90°,EF过
点C,BE⊥EF于点E,DF⊥EF于点F,BE=
DF,求证:△BCE2△DCF.
证明:连接AC,在Rt△ABC
和Rt△ADC中,
B
.AB=AD,AC=AC,
.'.Rt∧ABC≌Rt入ADC(HI),
E
。。BC=DC,
.BE⊥EF,DF⊥EF,.∠E=∠F=90°.
在Rt△BCE和Rt人DCF中,
BC=DC,
BE=DF,
..Rt人BCE≌RtDCF(HL).
