【2023版】人教版数学八上-第12章 全等三角形 专题训练(三) 与角平分线有关的全等证明的三种类型 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第12章 全等三角形 专题训练(三) 与角平分线有关的全等证明的三种类型 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
专题训练(三)与角平分线有关的全等证明
的三种类型
第十二章 全等三角形
必
●
类型1
过角的平分线上的点向角的两边作
垂线构造“AAS”型全等
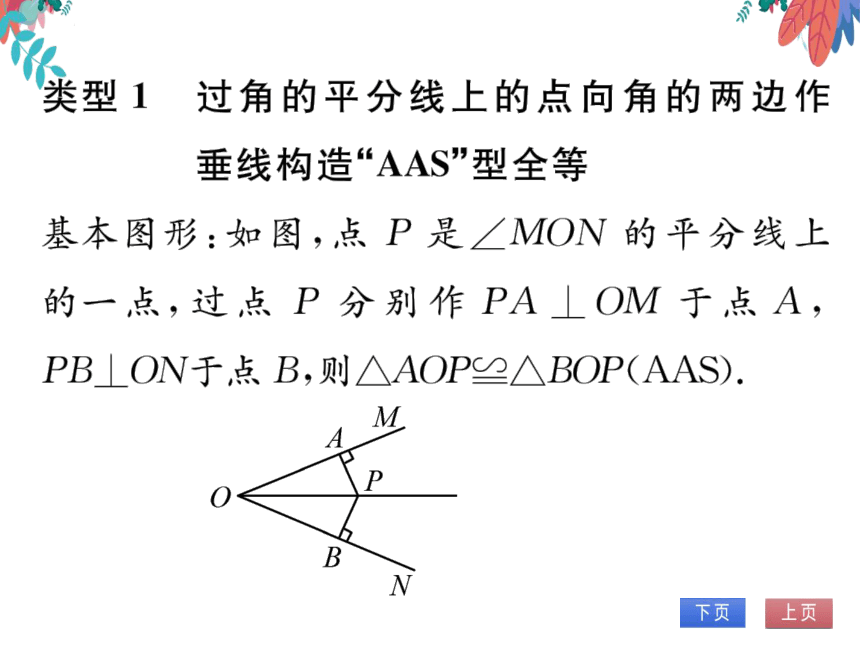
基本图形:如图,点P是∠MON的平分线上
的一,点,过点P分别作PA OM于点A,
PBON于,点B,则AOP≌BOP(AAS).
M
A
P
B
W
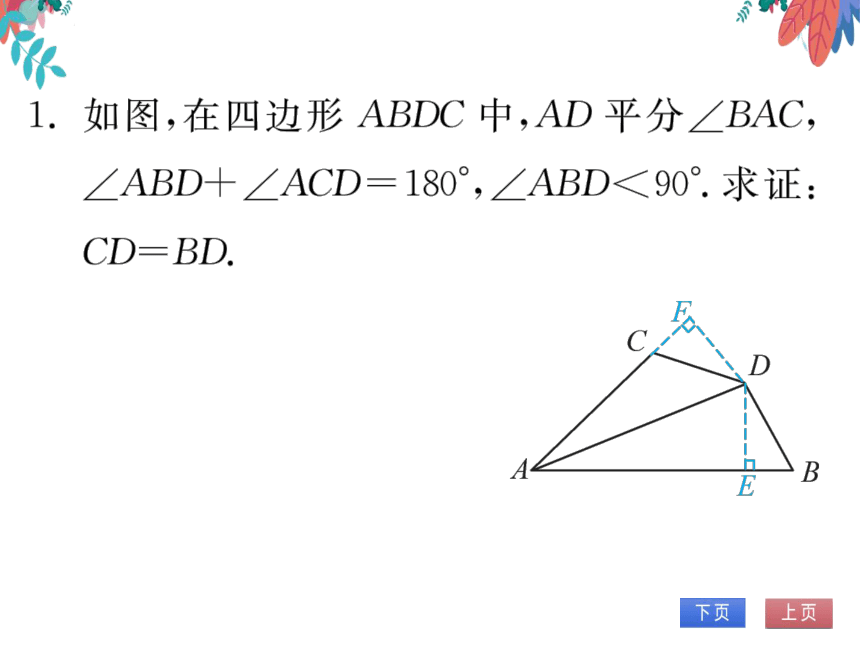
1.如图,在四边形ABDC中,AD平分∠BAC,
∠ABD十∠ACD=180°,∠ABD≤90°.求证:
CD-BD.
证明:如图,过点D分别
作DE⊥AB于点E,DF
⊥AC于点F,则∠DEB
B
=/F=90°..·/ABD十/ACD=180°,
∠ACD+∠FCD=180°,
。∠ABD=∠FCD..°AD平分∠BAC,
DEAB,DFAC,。.DE=DF.
∠F=∠DEB=0°,
在人DCF和△DBE中,∠FCD=∠ABD,
DF=DE,
..人DCF≌人DBE(AAS)..CD=BD.
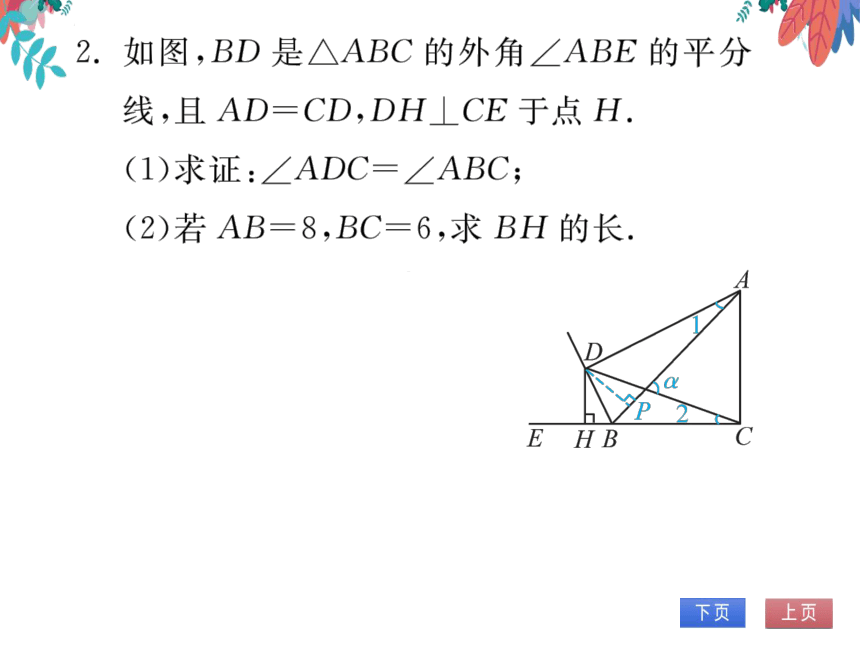
DH=DP,
在Rt人DHC和Rt人DPA中,
CD-AD,
.'.Rt△DHC≌RtADPA(HL).
。∠1=∠2.
又,'∠1+∠ADC=∠2+∠ABC=a,
,.∠ADC=∠ABC.
∠DHB=∠DPB=90°,
∠DBH=∠DBP,
BD=BD,
.'.△DBH≌∧DBP(AAS).
。。DH=DP,BH=BP.
(2)解:由(1)知HD=BP,设HB=bP=x,
则CH=x十BC=6十x,AP=AB一x=8一x.
.Rt∧DHC≌Rt人DPA,.CH=AP.
。.6十x=8一x。。。x=1.故BH的长为1.
3.如图,在△ABC中,AD是∠BAC的平分
线,BE⊥AD于点E.探究∠ABE,
∠DBE,∠C之间的数量关系.
解:∠ABE=∠DBE十∠C,
理由如下:
如图,延长BE交AC于点F,
AD是∠BAC的平分线,
∠BAE=∠FAE,
AE=AE,
AEB-/AEF,
..△ABE≌人AFE(ASA).
。。∠ABE=∠AFE.
.·∠AFE=∠DBE十∠C,
°。∠ABE=∠DBE十∠C.
4.如图,已知等腰直角三角形ABC中,
∠BAC=90°,AB=AC,BD平分∠ABC,
CE⊥BD交BD的延长线于点E.求证:
BD=2CE.
在Rt△BAD和Rt△CAF中,
(∠BAD=∠CAF=90°,
AB=AC,
、/ABD=∠ECD,
..Rt人BAD≌Rt△CAF(ASA).
。。BD=CF。
专题训练(三)与角平分线有关的全等证明
的三种类型
第十二章 全等三角形
必
●
类型1
过角的平分线上的点向角的两边作
垂线构造“AAS”型全等
基本图形:如图,点P是∠MON的平分线上
的一,点,过点P分别作PA OM于点A,
PBON于,点B,则AOP≌BOP(AAS).
M
A
P
B
W
1.如图,在四边形ABDC中,AD平分∠BAC,
∠ABD十∠ACD=180°,∠ABD≤90°.求证:
CD-BD.
证明:如图,过点D分别
作DE⊥AB于点E,DF
⊥AC于点F,则∠DEB
B
=/F=90°..·/ABD十/ACD=180°,
∠ACD+∠FCD=180°,
。∠ABD=∠FCD..°AD平分∠BAC,
DEAB,DFAC,。.DE=DF.
∠F=∠DEB=0°,
在人DCF和△DBE中,∠FCD=∠ABD,
DF=DE,
..人DCF≌人DBE(AAS)..CD=BD.
DH=DP,
在Rt人DHC和Rt人DPA中,
CD-AD,
.'.Rt△DHC≌RtADPA(HL).
。∠1=∠2.
又,'∠1+∠ADC=∠2+∠ABC=a,
,.∠ADC=∠ABC.
∠DHB=∠DPB=90°,
∠DBH=∠DBP,
BD=BD,
.'.△DBH≌∧DBP(AAS).
。。DH=DP,BH=BP.
(2)解:由(1)知HD=BP,设HB=bP=x,
则CH=x十BC=6十x,AP=AB一x=8一x.
.Rt∧DHC≌Rt人DPA,.CH=AP.
。.6十x=8一x。。。x=1.故BH的长为1.
3.如图,在△ABC中,AD是∠BAC的平分
线,BE⊥AD于点E.探究∠ABE,
∠DBE,∠C之间的数量关系.
解:∠ABE=∠DBE十∠C,
理由如下:
如图,延长BE交AC于点F,
AD是∠BAC的平分线,
∠BAE=∠FAE,
AE=AE,
AEB-/AEF,
..△ABE≌人AFE(ASA).
。。∠ABE=∠AFE.
.·∠AFE=∠DBE十∠C,
°。∠ABE=∠DBE十∠C.
4.如图,已知等腰直角三角形ABC中,
∠BAC=90°,AB=AC,BD平分∠ABC,
CE⊥BD交BD的延长线于点E.求证:
BD=2CE.
在Rt△BAD和Rt△CAF中,
(∠BAD=∠CAF=90°,
AB=AC,
、/ABD=∠ECD,
..Rt人BAD≌Rt△CAF(ASA).
。。BD=CF。
