【2023版】人教版数学八上-第13章 轴对称 13.1.2 第1课时 线段的垂直平分线的性质与判定 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第13章 轴对称 13.1.2 第1课时 线段的垂直平分线的性质与判定 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览






文档简介
(共21张PPT)
13.1.2第1课时 线段的垂直平分线
的性质与判定
第十三章 轴对称
必
●
C
B
1
12
(第1题图)
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1线段的垂直平分线的性质
1.如图,已知线段AB,BC的垂直平分线l1,
L2交于点M,则线段AM,CM的大小关系
是
B
A.AMCM
B.AM-CM
C.AMD.无法确定
2.(2022·湖北黄石)如图,在△ABC中,分别
以A,C为圆心,大于2AC长为半径作弧,
两弧分别相交于M,V两点,作直线MN,
分别交线段BC,AC于点D,E,若AE=
2cm,△ABD的周长为11cm,则△ABC
的周长为
(C)
A.13 cm B.14 cm C.15 cm D.16 cm
B
(第2题图)
3.(2022秋·海淀区校级月考)如
图,线段AB、BC的垂直平分线
L、l2相交于点O,若∠1=36°,B
则∠A0℃的度数是72°
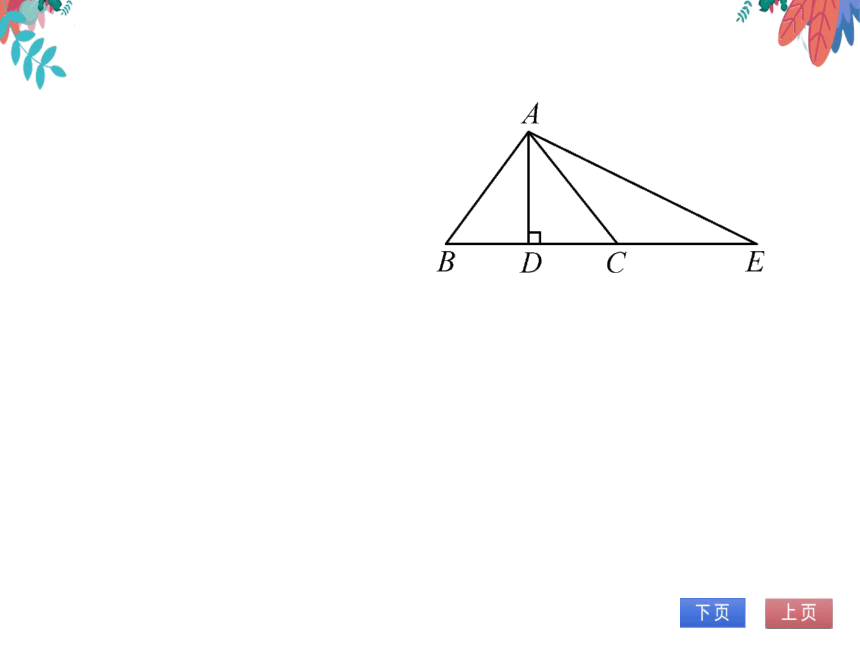
4.如图,AD⊥BC,BD=CD,点C在AE的垂
直平分线上,若AB=5cm,BD=3cm,求
BE的长.
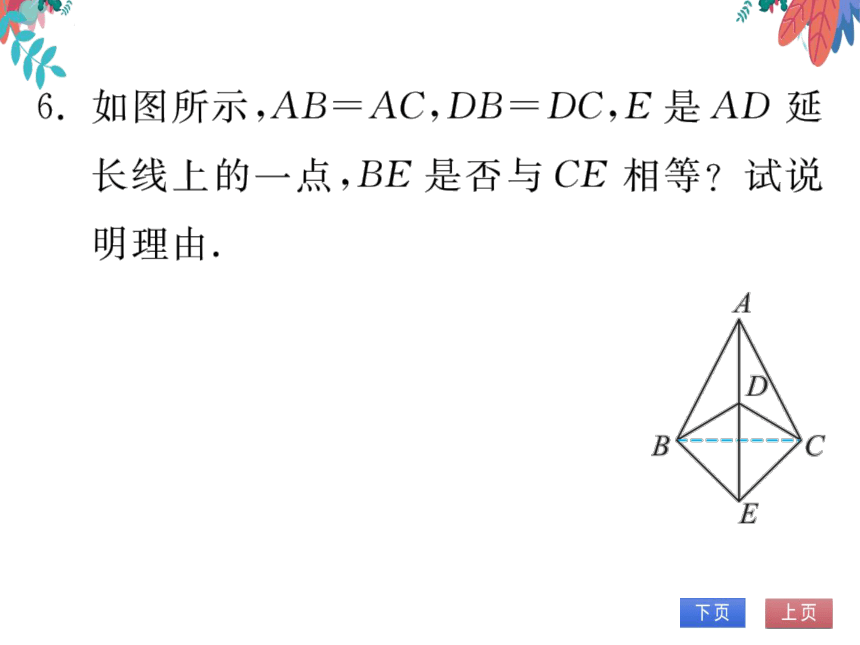
。两点确定一条直线,
·AD是线段BC的垂直平分线.
.E是AD延长线上的一点,
。。BE=CE.
知识点3
利用尺规作已知直线的垂线
7.如图,已知钝角△ABC,其中∠A是钝角,
求作AC边上的高BH.(尺规作图,保留作
图痕迹,不写过程)
解:如图示,BH即为
B
所求.
规律方法全练
提升能力
o00000000000000000000000000000000000
8.如图,OP平分∠MON,点
M
C为OP上的任意一点,
CAOV,垂足为A,线段
A
N
OA的垂直平分线BG交OM于点B,交OA
于点G,已知AB=6,AC=3,则△OBC的面
积为
9
9.(2022·香坊区一模)在Rt△ABC中,
∠ABC=90°,斜边AC的垂直平分线交射
线CB于点E,交射线AB于点F,若AB=
4,BE=3,则线段BF的长为
1.5或6
10.(2021秋·大余县期末)如图,AD是
△ABC的角平分线,DE、DF分别是
△ABD和△ACD的高,求证:AD垂直平
分EF.
证明:设AD、EF的交点为
K,,AD平分∠BAC,DE
AB,DFAC,。'.DE=DF.
B
13.1.2第1课时 线段的垂直平分线
的性质与判定
第十三章 轴对称
必
●
C
B
1
12
(第1题图)
知识要点全练
夯实基础
o00000000000000000000000000000000000
知识点1线段的垂直平分线的性质
1.如图,已知线段AB,BC的垂直平分线l1,
L2交于点M,则线段AM,CM的大小关系
是
B
A.AMCM
B.AM-CM
C.AM
2.(2022·湖北黄石)如图,在△ABC中,分别
以A,C为圆心,大于2AC长为半径作弧,
两弧分别相交于M,V两点,作直线MN,
分别交线段BC,AC于点D,E,若AE=
2cm,△ABD的周长为11cm,则△ABC
的周长为
(C)
A.13 cm B.14 cm C.15 cm D.16 cm
B
(第2题图)
3.(2022秋·海淀区校级月考)如
图,线段AB、BC的垂直平分线
L、l2相交于点O,若∠1=36°,B
则∠A0℃的度数是72°
4.如图,AD⊥BC,BD=CD,点C在AE的垂
直平分线上,若AB=5cm,BD=3cm,求
BE的长.
。两点确定一条直线,
·AD是线段BC的垂直平分线.
.E是AD延长线上的一点,
。。BE=CE.
知识点3
利用尺规作已知直线的垂线
7.如图,已知钝角△ABC,其中∠A是钝角,
求作AC边上的高BH.(尺规作图,保留作
图痕迹,不写过程)
解:如图示,BH即为
B
所求.
规律方法全练
提升能力
o00000000000000000000000000000000000
8.如图,OP平分∠MON,点
M
C为OP上的任意一点,
CAOV,垂足为A,线段
A
N
OA的垂直平分线BG交OM于点B,交OA
于点G,已知AB=6,AC=3,则△OBC的面
积为
9
9.(2022·香坊区一模)在Rt△ABC中,
∠ABC=90°,斜边AC的垂直平分线交射
线CB于点E,交射线AB于点F,若AB=
4,BE=3,则线段BF的长为
1.5或6
10.(2021秋·大余县期末)如图,AD是
△ABC的角平分线,DE、DF分别是
△ABD和△ACD的高,求证:AD垂直平
分EF.
证明:设AD、EF的交点为
K,,AD平分∠BAC,DE
AB,DFAC,。'.DE=DF.
B
