【2023版】人教版数学八上-第12章 全等三角形 专题训练(二) 证明三角形全等的基本模型 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第12章 全等三角形 专题训练(二) 证明三角形全等的基本模型 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览




文档简介
(共29张PPT)
专题训练(二) 证明三角形全等的基本模型
第十二章 全等三角形
必
●
类型1手拉手模型
1.已知在△ABC和△AEF中,AB=AC,AE=
AF,∠CAB=∠EAF,BE交FC于O点.
(1)如图1,当∠CAB=90°时,求证:BE=
CF,BE CF;
E
B
A
F
图1
(2)如图2,当∠CAB=60°时,求∠BOC的
度数;
(3)猜想:当∠CAB=a时(0°<&<90),
∠BOC的度数为
·(用含a的
式子表示)
C
A
B
图2
(1)证明:.∠CAD=∠EAF,
..∠CAB十∠CAE=∠EAF十∠CAE,即
∠BAE=∠CAF,在△ABE与△ACF中,
AB=AC,
/BAE=∠CAF,.'.∧ABE≌△ACF(SAS),
AE=AF,
..BE=CF,∠ACF=∠ABE.
./BAC=90°,
.'.∠BCA+∠ABE+∠OBC=∠BCA+∠ACF
+∠OBC=/BCOH/OBC=90°.
.∠BOC=0°,即BE⊥CF;
(2)解:同(1)可得△BAE2入CAF,
。∠ABE=∠ACF,
∠BCO+∠CBO=∠ACO+∠ACD+
∠CBO=∠ACB十∠ABO十/CBO=
∠ACB+∠ABC=180°-60°=120°,
。。∠BOC=60°;
(3)a.
类型2三垂直模型
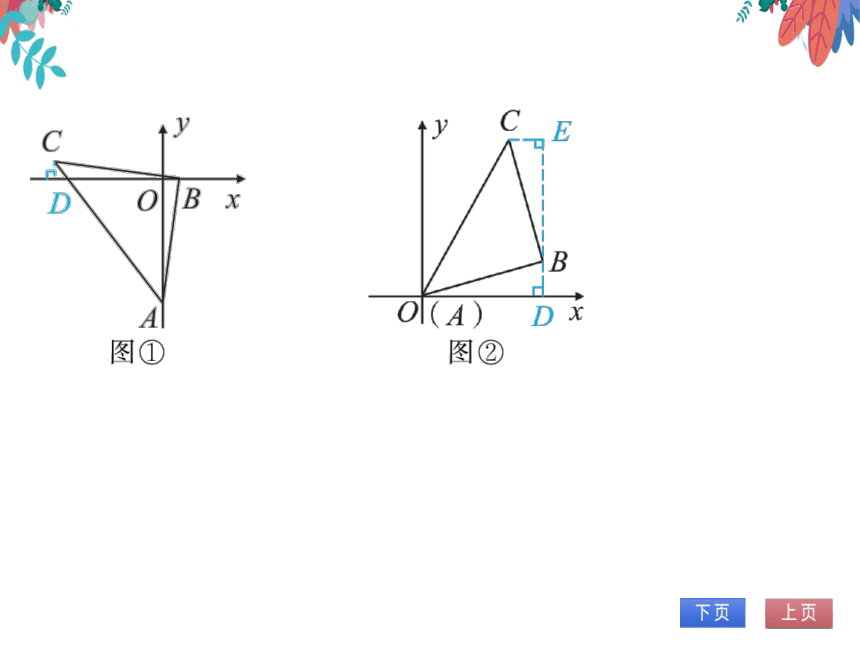
2.已知△ABC在平面直角坐标系中,在
△ABC中,AB=BC,∠ABC=90°.
(1)如图①,已知点A(0,一4),B(1,0),求
点C的坐标;
(2)如图②,已知点A(0,0),B(3,1),求点
C的坐标.
C
C
E
D
B
B
A
O(A)
D
X
图①
图②
解:(1)过点C作CD⊥x轴于点D,则
∠DBC+∠DCB=90°.
.∠ABC=0°,。∠DBC+∠ABD=90°,
.∠DCB=∠ABD.
又.AB=BC,∠AOD=∠BDC=90°,
.△CDB≌∧BOA(AAS).
。'。CD=OB=1,BD=OA=4.。.OD=3.
.点C的坐标为(一3,1);
又.AB=BC,∠ADB=∠BEC=90°,
,.人ABD2△BCE(AAS).
.'.AD=EB=3,BD=CE=1,..DE=4.
.点C的坐标为(2,4).
(2)过点D作BD⊥x轴于点D,过点C作
CEDB,交DB的延长线于点E,则∠ADB
=∠BC=0°,∠BAD十/ABD=0°.
.∠ABC=0°,.∠ABD十∠EBC=90°,
,∠BAD=∠EBC.
专题训练(二) 证明三角形全等的基本模型
第十二章 全等三角形
必
●
类型1手拉手模型
1.已知在△ABC和△AEF中,AB=AC,AE=
AF,∠CAB=∠EAF,BE交FC于O点.
(1)如图1,当∠CAB=90°时,求证:BE=
CF,BE CF;
E
B
A
F
图1
(2)如图2,当∠CAB=60°时,求∠BOC的
度数;
(3)猜想:当∠CAB=a时(0°<&<90),
∠BOC的度数为
·(用含a的
式子表示)
C
A
B
图2
(1)证明:.∠CAD=∠EAF,
..∠CAB十∠CAE=∠EAF十∠CAE,即
∠BAE=∠CAF,在△ABE与△ACF中,
AB=AC,
/BAE=∠CAF,.'.∧ABE≌△ACF(SAS),
AE=AF,
..BE=CF,∠ACF=∠ABE.
./BAC=90°,
.'.∠BCA+∠ABE+∠OBC=∠BCA+∠ACF
+∠OBC=/BCOH/OBC=90°.
.∠BOC=0°,即BE⊥CF;
(2)解:同(1)可得△BAE2入CAF,
。∠ABE=∠ACF,
∠BCO+∠CBO=∠ACO+∠ACD+
∠CBO=∠ACB十∠ABO十/CBO=
∠ACB+∠ABC=180°-60°=120°,
。。∠BOC=60°;
(3)a.
类型2三垂直模型
2.已知△ABC在平面直角坐标系中,在
△ABC中,AB=BC,∠ABC=90°.
(1)如图①,已知点A(0,一4),B(1,0),求
点C的坐标;
(2)如图②,已知点A(0,0),B(3,1),求点
C的坐标.
C
C
E
D
B
B
A
O(A)
D
X
图①
图②
解:(1)过点C作CD⊥x轴于点D,则
∠DBC+∠DCB=90°.
.∠ABC=0°,。∠DBC+∠ABD=90°,
.∠DCB=∠ABD.
又.AB=BC,∠AOD=∠BDC=90°,
.△CDB≌∧BOA(AAS).
。'。CD=OB=1,BD=OA=4.。.OD=3.
.点C的坐标为(一3,1);
又.AB=BC,∠ADB=∠BEC=90°,
,.人ABD2△BCE(AAS).
.'.AD=EB=3,BD=CE=1,..DE=4.
.点C的坐标为(2,4).
(2)过点D作BD⊥x轴于点D,过点C作
CEDB,交DB的延长线于点E,则∠ADB
=∠BC=0°,∠BAD十/ABD=0°.
.∠ABC=0°,.∠ABD十∠EBC=90°,
,∠BAD=∠EBC.
