【2023版】人教版数学八上-第13章 轴对称 13.3.2 第1课时 等边三角形的性质与判定 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第13章 轴对称 13.3.2 第1课时 等边三角形的性质与判定 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览




文档简介
(共17张PPT)
13.3.2第1课时 等边三角形的性质与判定
第十三章 轴对称
必
●
知识要点全练
夯实基础
ooooooooooooooooooooooooooooooooooo
知识点1
等边三角形的性质
1.如图,在等边三角形ABC中,ADBC,垂
足为D,点E在线段AD上,∠EBC=45°,
则∠ACE等于
(A)
A.15°
B.309
C.45°
D.60°
A
E
B
D
C
(第1题图)
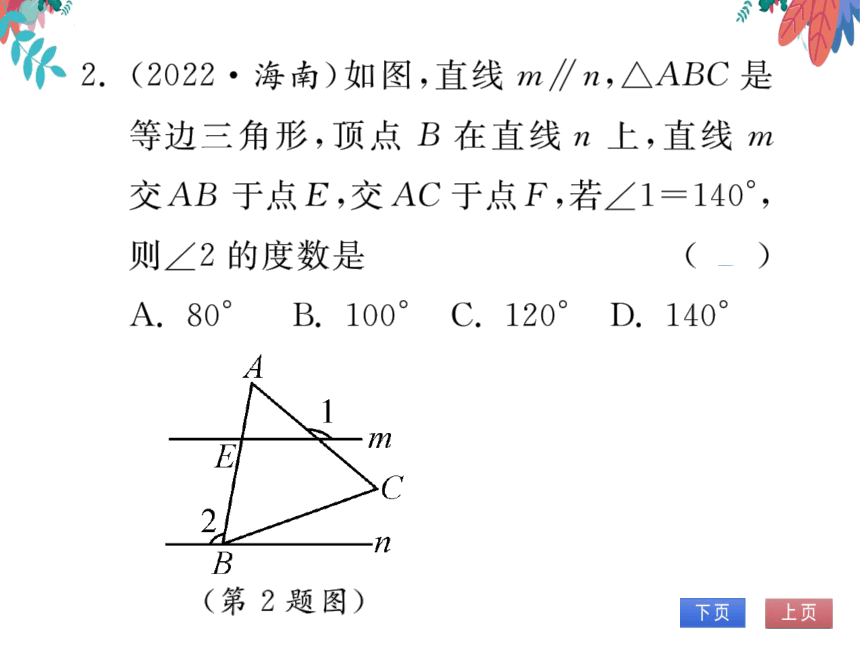
2.(2022·海南)如图,直线m∥n,△ABC是
等边三角形,顶点B在直线n上,直线m
交AB于点E,交AC于点F,若∠1=140°,
则∠2的度数是
B
A.80°
B.100°
C.120°
D.140
A
2
E
C
2
n
B
(第2题图)
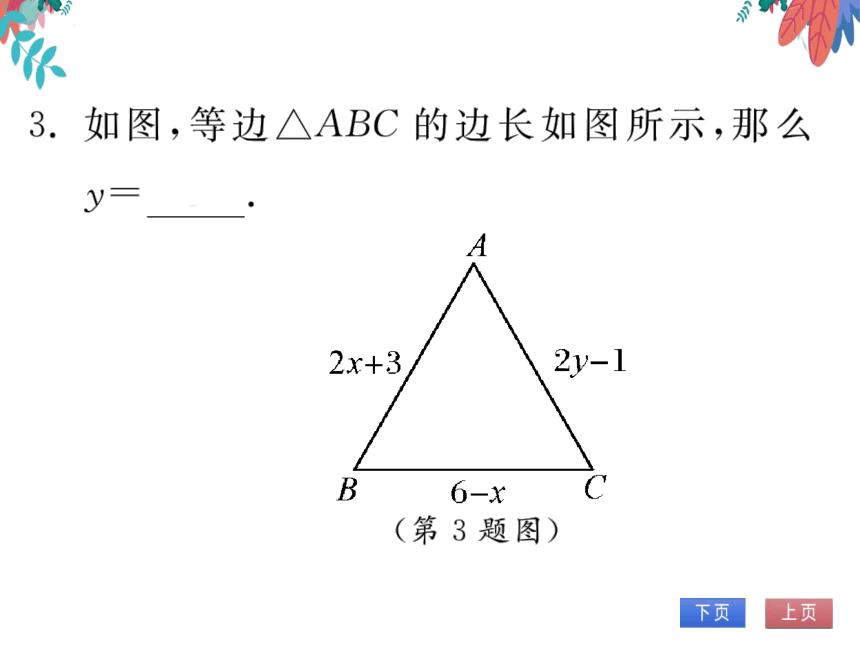
2x+3
2y-1
B
6-x
C
(第3题图)
4.如图,△ABC为等边三角形,AD平分∠BAC
△ADE是等边三角形,下列结论:①AD
BC;②EF=FD;③BE=BD;④∠ABE=60°.其
中正确的有
①②③④.(填序号)
A
E
F
B
D
C
(第4题图)
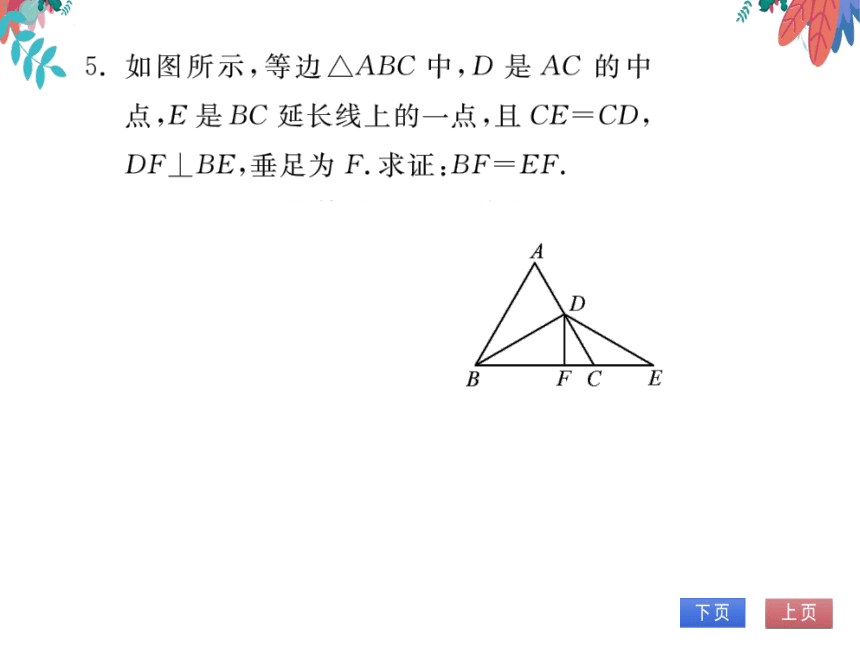
5.如图所示,等边△ABC中,D是AC的中
点,E是BC延长线上的一点,且CE=CD,
DFBE,垂足为F.求证:BF=EF.
证明:,BD是等边人ABC的中线,·。BD
平分∠ABC...∠DBE
1
∠ABC=30°.·CE=
2
B
F C
E
CD,∠E=3∠ACB
30°.。∠DBE=∠E.。。DB=DE.。DF
BE,.DF为等腰三角形底边上的中线.
。°。BF=EF.
6.如图,在人ABC中,AB=AC,D为AC的中点,
DEAB,DF⊥BC,垂足分别为E,F,且DE=
DF.求证:△ABC是等边三角形.
证明:,AB=AC,
E
。/B=/C
DE AB,DF BC,
B
.'./DEA=/DFC=0°.
,D为AC的中点,.DA=DC.
7.如图所示,锐角△ABC中,∠A=60°,它的
两条高BD,CE相交于点O,且OB=OC,
求证:人ABC是等边三角形.
证明:,OB=OC,
./OBC=∠OCB.
,·锐角△ABC的两条高BC、CE相交
于点O,
B
..∠BEC=∠BDC=90°.
·∠BOE=∠COD,.∠EBO=∠DCO.∴.∠ABC=
∠ACB..AB=AC..△ABC是等腰三角形。
又∠A=60°..△ABC是等边三角形.
13.3.2第1课时 等边三角形的性质与判定
第十三章 轴对称
必
●
知识要点全练
夯实基础
ooooooooooooooooooooooooooooooooooo
知识点1
等边三角形的性质
1.如图,在等边三角形ABC中,ADBC,垂
足为D,点E在线段AD上,∠EBC=45°,
则∠ACE等于
(A)
A.15°
B.309
C.45°
D.60°
A
E
B
D
C
(第1题图)
2.(2022·海南)如图,直线m∥n,△ABC是
等边三角形,顶点B在直线n上,直线m
交AB于点E,交AC于点F,若∠1=140°,
则∠2的度数是
B
A.80°
B.100°
C.120°
D.140
A
2
E
C
2
n
B
(第2题图)
2x+3
2y-1
B
6-x
C
(第3题图)
4.如图,△ABC为等边三角形,AD平分∠BAC
△ADE是等边三角形,下列结论:①AD
BC;②EF=FD;③BE=BD;④∠ABE=60°.其
中正确的有
①②③④.(填序号)
A
E
F
B
D
C
(第4题图)
5.如图所示,等边△ABC中,D是AC的中
点,E是BC延长线上的一点,且CE=CD,
DFBE,垂足为F.求证:BF=EF.
证明:,BD是等边人ABC的中线,·。BD
平分∠ABC...∠DBE
1
∠ABC=30°.·CE=
2
B
F C
E
CD,∠E=3∠ACB
30°.。∠DBE=∠E.。。DB=DE.。DF
BE,.DF为等腰三角形底边上的中线.
。°。BF=EF.
6.如图,在人ABC中,AB=AC,D为AC的中点,
DEAB,DF⊥BC,垂足分别为E,F,且DE=
DF.求证:△ABC是等边三角形.
证明:,AB=AC,
E
。/B=/C
DE AB,DF BC,
B
.'./DEA=/DFC=0°.
,D为AC的中点,.DA=DC.
7.如图所示,锐角△ABC中,∠A=60°,它的
两条高BD,CE相交于点O,且OB=OC,
求证:人ABC是等边三角形.
证明:,OB=OC,
./OBC=∠OCB.
,·锐角△ABC的两条高BC、CE相交
于点O,
B
..∠BEC=∠BDC=90°.
·∠BOE=∠COD,.∠EBO=∠DCO.∴.∠ABC=
∠ACB..AB=AC..△ABC是等腰三角形。
又∠A=60°..△ABC是等边三角形.
