【2023版】人教版数学八上-第13章 轴对称 13.3.1 第1课时 等腰三角形的性质 习题课件
文档属性
| 名称 | 【2023版】人教版数学八上-第13章 轴对称 13.3.1 第1课时 等腰三角形的性质 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-14 09:37:00 | ||
图片预览





文档简介
(共22张PPT)
13.3.1第1课时 等腰三角形的性质
第十三章 轴对称
必
●
知识要点全练
夯实基础
o0000000oooooooooooooooooooooooooooo
知识点1
等边对等角
1.若等腰三角形的一个角是80°,则它的顶角
的度数是
(B)
A.80°
B.20°或809
C.20°
D.50°或80°
2.(2022·青海)如图,在Rt△ABC中,
∠ABC=90°,ED是AC的垂直平分线,交
AC于点D,交BC于点E,∠BAE=10°,
则∠C的度数是
40°
A
D
BE
C
(第2题图)
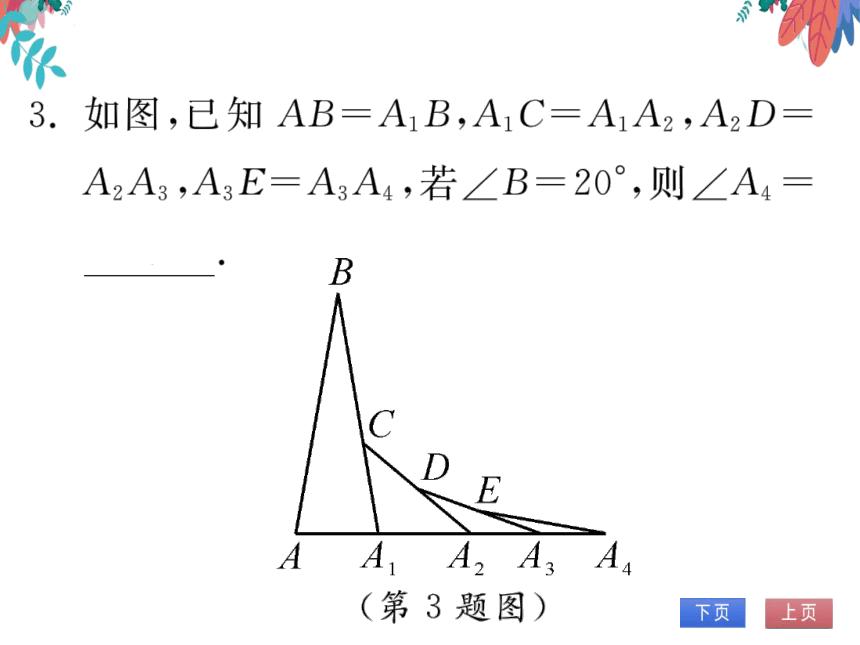
3.如图,已知AB=A1B,A1C=A1A2,A2D=
A2A3,A3E=A3A4,若∠B=20°,则∠A4=
10°
B
C
D
E
A
A A2 A3 A
(第3题图)
4.已知一个等腰三角形的两角分别为(2x一2)°,
(3x一5)°,求这个等腰三角形各角的度数.
解:①当(2x一2)°为顶角时,即(2x一2)十2
X(3x一5)=180,解得x=24,等腰三角形
三个角的度数分别为46°,67°,67°。
②当(3x一5)°为顶角时,即(3x一5)十2×
(2x一2)=180,解得x=27,等腰三角形三
个角的度数分别为52°,52°,76°.
③当以上两个角均为底角时,即(2x一2)=(3x
一5),解得x=3,等腰三角形三个角的度数分
别为4°,4°,172°.
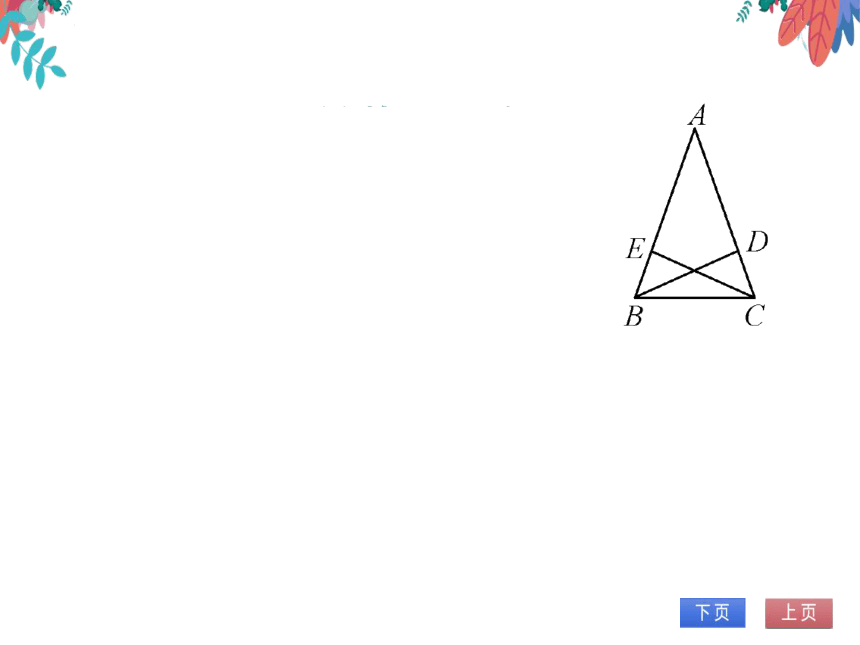
5.(2022·山东淄博)如图,△ABC是等腰三
角形,点D,E分别在腰AC,AB上,且
BE=CD,连接BD,CE.求证:BD=CE.
证明:。·人ABC是等腰三角形,
。∠EBC=∠DCB,
在△EBC与人DCB中
BE=CD,
B
∠EBC=∠DCB,
BC=CB,
。.△EBC≌△DCB(SAS),.'.BD=CE.
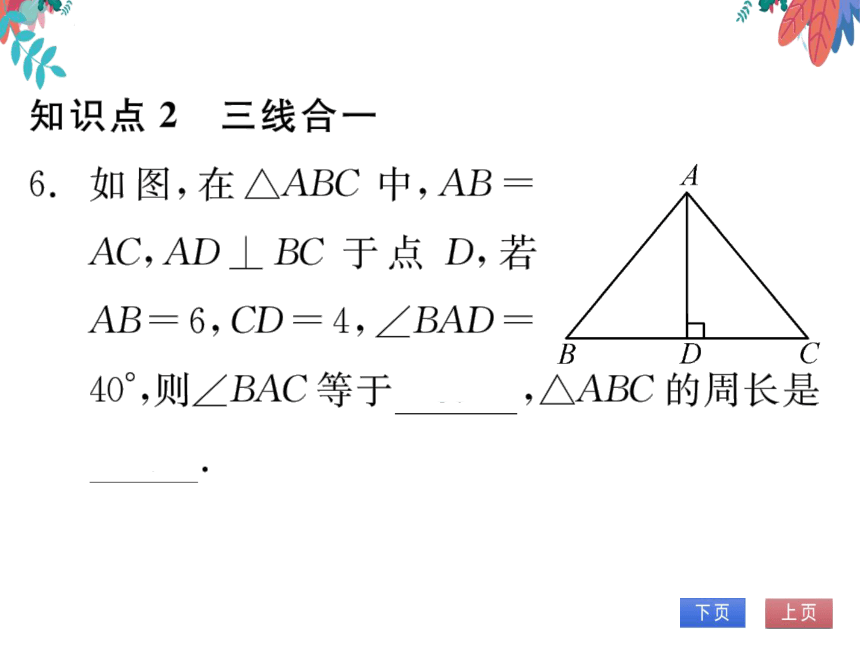
知识点2三线合一
6.如图,在△ABC中,AB=
AC,AD⊥BC于点D,若
AB=6,CD=4,∠BAD=
B
D
40°,则∠BAC等于80°,△ABC的周长是
20
7.如图,在△ABC中,AB=AC,D为BC的
中点,DE⊥AB.
(1)求证:∠BAC=2∠EDB;
(2)若AC=4,DE=3,求△ABC的面积.
(1)证明:,°AC=AB,CD=
BD,.∠DAC=∠DAB,AD1
BC.。DEAB,
A
E B
.∠DAB十∠B=∠EDB十∠B=90°.
.∠EDB=∠DAB=∠DAC.
。'.∠BAC=2∠EDB.
13.3.1第1课时 等腰三角形的性质
第十三章 轴对称
必
●
知识要点全练
夯实基础
o0000000oooooooooooooooooooooooooooo
知识点1
等边对等角
1.若等腰三角形的一个角是80°,则它的顶角
的度数是
(B)
A.80°
B.20°或809
C.20°
D.50°或80°
2.(2022·青海)如图,在Rt△ABC中,
∠ABC=90°,ED是AC的垂直平分线,交
AC于点D,交BC于点E,∠BAE=10°,
则∠C的度数是
40°
A
D
BE
C
(第2题图)
3.如图,已知AB=A1B,A1C=A1A2,A2D=
A2A3,A3E=A3A4,若∠B=20°,则∠A4=
10°
B
C
D
E
A
A A2 A3 A
(第3题图)
4.已知一个等腰三角形的两角分别为(2x一2)°,
(3x一5)°,求这个等腰三角形各角的度数.
解:①当(2x一2)°为顶角时,即(2x一2)十2
X(3x一5)=180,解得x=24,等腰三角形
三个角的度数分别为46°,67°,67°。
②当(3x一5)°为顶角时,即(3x一5)十2×
(2x一2)=180,解得x=27,等腰三角形三
个角的度数分别为52°,52°,76°.
③当以上两个角均为底角时,即(2x一2)=(3x
一5),解得x=3,等腰三角形三个角的度数分
别为4°,4°,172°.
5.(2022·山东淄博)如图,△ABC是等腰三
角形,点D,E分别在腰AC,AB上,且
BE=CD,连接BD,CE.求证:BD=CE.
证明:。·人ABC是等腰三角形,
。∠EBC=∠DCB,
在△EBC与人DCB中
BE=CD,
B
∠EBC=∠DCB,
BC=CB,
。.△EBC≌△DCB(SAS),.'.BD=CE.
知识点2三线合一
6.如图,在△ABC中,AB=
AC,AD⊥BC于点D,若
AB=6,CD=4,∠BAD=
B
D
40°,则∠BAC等于80°,△ABC的周长是
20
7.如图,在△ABC中,AB=AC,D为BC的
中点,DE⊥AB.
(1)求证:∠BAC=2∠EDB;
(2)若AC=4,DE=3,求△ABC的面积.
(1)证明:,°AC=AB,CD=
BD,.∠DAC=∠DAB,AD1
BC.。DEAB,
A
E B
.∠DAB十∠B=∠EDB十∠B=90°.
.∠EDB=∠DAB=∠DAC.
。'.∠BAC=2∠EDB.
